Фінансовий менеджмент - Шелудько В.М. - Практикум

Завдання 1

Облігацію з фіксованим купоном 11 %, що сплачується раз на рік. передбачено погасити 01.12.2008 р. за номінальною вартістю 1000 грн.

Визначити;

1) ринкову вартість облігації після сплати за нею процентів 01.12.2004 р., якщо дохідність &0подібних облігацій, що в даний момент перебувають в обігу на ринку, становить 9 %. Наступні купонні виплати за облігацією буде здійснено через рік;

2) яку суму повинен сплатити інвестор власнику облігації при купівлі її 05.05.2005 р., якщо останні купонні виплати відбулися 01.12.2004 р., ринкова дохідність подібних облігацій, що в даний момент перебувають в обігу на ринку, становить 12 %;

3) яку дохідність забезпечить облігація інвестору, якщо її придбано 01.12.2004 після сплати за нею процентів за ринковою ціною 980 грн;

4) чи забезпечить облігація інвестору дохідність на рівні 11,5 %, якщо придбати її за ринковою ціною 990 грн 01.12.2004 р. після сплати за нею процентів?

Розв'язування

1. Очікувані грошові потоки за облігацією складаються з чотирикратних купонних виплат у розмірі 110 грн та суми 1000 грн, яку отримає власник облігації 01.12.2008 при її погашенні.

Для визначення ринкової вартості облігації необхідно дисконтувати ці грошові потоки на дату 01.12.2004 р. за ставкою к0 = 9 %, яка визначає дохідність подібних облігацій:

2. Для того щоб визначити ціну продажу облігації на ринку 05.05.2005 р., коли з моменту останніх купонних виплат минуло 155 днів, а до наступних виплат залишилося 210 днів, треба розрахувати теперішню вартість очікуваних грошових потоків за облігацією за формулою (7.21), а також накопичений власником облігації за 155 днів процент /:

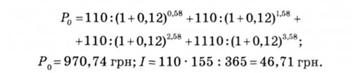
Придбати облігацію на ринку можна згідно (7.22) за ціною: Р*~ 970,74 4- 46,71 = 1017,45 грн, що компенсує її попередньому власнику втрати від володіння облігацією протягом 155 днів без можливості отримати наступні купонні виплати.

3. Для визначення очікуваної дохідності облігації при відомій її ринковій вартості необхідно розв'язати рівняння (7.20) відносно к :

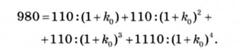
Рівняння такого типу мають аналітичний розв'язок лише в окремих випадках. Для розв'язування рівняння використовують фінансовий калькулятор або комп'ютер. Розв'язком рівняння є процентна ставка к0 = 0,1165, або к0= 11,65 %. Якщо інвестор придбає облігацію 01.12.2004 р. після сплати за нею процентів за ціною 980 грн, облігація забезпечить йому дохідність на рівні 11,65 %, що на 0,65 % вище від купонної ставки.

4. Для того щоб відповісти на запитання, чи забезпечить облігація інвестору дохідність на рівні 11,6 %, якщо придбати її 01.12.2004 р. за ринковою вартістю 990 грн після сплати за нею процентів, необхідно розв'язати відносно £0 рівняння:

Визначити:

1) нарощені протягом року суми та процентний дохід у разі нарахування простоїте складної ставки процентів, якщо проценти нараховуються раз на квартал;

2) ефективну процентну ставку в разі нарахування складних процентів.

Розв'язування

Використовуючи формули (7.9) та (7.12) послідовно для чотирьох періодів (кварталів), отримаємо нарощені протягом року суми в разі нарахування простих (Св) і складних (Сс) процентів:

Процентний дохід у разі нарахування простих (/ )і складних (/.) процентів визначається різницею між нарощеними та початково внесеними сумами:

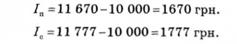
Оскільки ефективна процентна ставка — це ставка, яка нараховується один раз на рік і забезпечує такий

самий рівень доходу, що й інші варіанти вкладення коштів, її можна визначити з рівності

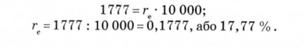
Завдання 4

Кредит у сумі 100 000 грн надано на чотири роки під 16 % річних з погашенням рівними частинами. Платежі в погашення кредиту сплачуються щороку.

Визначити частину основної суми боргу, що погашається в кожному з періодів та проценти за кожний період.

Розв'язування

Платежі в погашення кредиту в цьому випадку однакові протягом усього періоду кредитування і містять різні частки основної суми боргу та процентів у погашення борту.

Припустимо, що періодичні платежі в погашення кредиту дорівнюють Б* Якщо к — процентна ставка за кредитом, п — строк кредитування, що визначає кількість періодів (років, кварталів чи місяців), аС—сума кредиту, то проценти, сплачені за перший період, становитимуть І, = Л • С. Платіж у погашення кредиту за перший період визначається сумою:

Зважаючи на те, що платіж у погашення кредиту є, з одного боку, постійною величиною, а з другого — визначається сумою:

Завдання 5

Протягом чотирьох місяців з 1 березня по 30 червня на початку кожного місяця на депозитний рахунок щомісяця вносились кошти в сумі С = 1000 грн. Процентна ставка протягом перших 50 днів становила 14 %, протягом наступних 72 днів — 16 % річних.

Обчислити суму нарахованих за чотири місяці процентів та нарощену суму, якщо банк нараховує за вкладом просту ставку процентів.

Розв'язування

Дохідність депозитних операцій залежить від суми вкладених коштів, методу нарахування процентів та частоти їх нарахування. Якщо на депозитному вкладі розміщено суму С, на яку щоперіоду нараховується проста ставка процентів, загальна сума процентних виплат становитиме:

Для визначення процентного доходу та нарощеної за чотири місяці суми відобразимо на часовій осі залишок коштів на рахунку на початок кожного місяця, процентні ставки та кількість днів у місяцях:

Завдання 6

Визначити нарощену суму та проценти за фінансовою рентою, якщо внески в сумі 10 000 грн було зроблено щороку протягом п'яти років. Процентна ставка за рентою становить 15 % річних.

Розв'язування

Припустимо, що кошти вносилися на рахунок протягом п років на початку кожного року в сумі Річна процентна ставка дорівнює к і нараховується у вигляді складних процентів. Суми внесків з нарахованими за відповідний період процентами на момент закінчення строку депозиту визначаються на основі формули (7.9) і відповідно дорівнюють:

Контрольні запитання і завдання

1. У чому полягає відмінність між номінальною та реальною процентними ставками?

2. Який існує взаємозв'язок між темпами зростання економіки та ринковими процентними ставками?

3. Як впливає інфляція на рівень ринкових процентних ставок?

4. Які основні складові премії за ризик в структурі процентної ставки?

Ь.Як пов'язані премія за ризик ліквідності та премія за ризик, пов'язаний зі строком обігу фінансового активу?

6. Яку процентну ставку називають безризиковою та як її визначають?

7. У чому полягає ризик неплатежу?

8. У чому суть фінансового ризику?

9. Який існує зв'язок міжризиковістю фінансових активів та ризиками в діяльності підприємств — емітентів фінансових активів?

10. Які величини необхідно знати для обчислення очікуваного доходу за портфелем фінансових активів?

11. Які основні причини широкого використання нормального розподілу в прикладних задачах?

12. Чому для оцінки ризику використовується стандартне відхилення?

13. Що відображує теперішня величина очікуваних грошових потоків за фінансовим активом?

14. Які існують підходи дооцінки ставки дисконтування очікуваних грошових потоків?

15. Які процентні ставки використовують як ставки дисконтування при оцінці інвестиційних проектів та фінансових активів?

16. У чому полягає оцінка фінансових активів?

17. Як коригується дохідність фінансових активів на первинному та вторинному ринках?

18. У чому полягають відмінності між купонною став кою та дохідністю облігації?

19. Як впливають зміни в ринкових процентних ставках на дохідність боргових зобов'язань, що перебувають в обігу на ринку?

20. Як залежить ринкова вартість облігації від строку її погашення?

21. Які чинники визначають ринкову вартість та дохідність акцій?

22. У чому полягає дивідендний метод оцінки акцій?

23. Які існують основні методи оцінки акцій?

24. У чому полягає метод дійсної вартості акції?