Фінансовий ринок - Шелудько В.М. - 8.3. Основні принципи ціноутворення у форвардних та ф'ючерсних контрактах

Розглянемо основні принципи ціноутворення та основні складові ф'ючерсних та форвардних цін. При цьому не будемо брати до уваги витрати на відкриття та закриття позиції у ф'ючерсному контракті чи інші витрати на проведення операцій. Не будемо враховувати і різницю у процентних ставках із залучення та інвестування коштів.

Нагадаємо, що базовими активами в форвардних контрактах можуть виступати різноманітні фінансові або матеріальні активи, валюта, процентні ставки, фондові індекси тощо. Ціноутворення в угодах на купівлю-продаж валюти чи в угодах про форвардні процентні ставки мають свою специфіку.

Розглянемо звичайну форвардну угоду на купівлю-продаж деякого фінансового активу X. Ціну активу, зафіксовану у форвардному контракті, називають ціною поставки (відповідно до дати поставки). Форвардною ціною називають ціну поставки у форвардних контрактах, які укладаються в даний момент. Щодня укладаються форвардні угоди і щодня змінюються не тільки ціни спот, а й форвардні ціни на ті чи інші активи. Чим ближче дати поставки, тим менша різниця між цінами на ринку спот та форвардними цінами.

При визначенні теоретичної форвардної ціни роблять два припущення:

• операція на форвардному ринку не здійснюється за власні кошти, тобто при проведенні операцій на форвардному ринку не здійснюється інвестування власних коштів, вони залучаються під деяку ринкову процентну ставку;

• фінансові результати від реалізації двох протилежних за змістом стратегій, які полягають у купівлі активу згідно з форвардним контрактом і безпосередній купівлі того самого активу на ринку, мають збігатися і дорівнювати нулю.

Це означає, що в цьому випадку неможливо здійснити арбітражну угоду й отримати арбітражний прибуток. Арбітражні угоди полягають у паралельному проведенні операцій на кількох ринках з метою отримання прибутку від різниці в ціпах па один і той самий актив на різних ринках. Причому не обов'язково, щоб це були однакові за своїм функціональним призначенням ринки (наприклад, купівля-продаж акцій на біржі в СІІІЛ і па біржі в Німеччині). Арбітражна угода може полягати і в паралельному проведенні операцій на ринках строкових угод та угод спот.

Визначення теоретичної форвардної ціни проілюструємо на прикладі. Ціна спот фінансового активу X становить 100 гр. од. За цим активом раз на квартал сплачується дохід у розмірі б гр. од. Форвардний контракт на актив X має дату поставки через три місяці. Ринкова процентна ставка з фінансування чи інвестування коштів на три місяці дорівнює 16% річних.

Розглянемо дві стратегії.

І. Припустимо, що форвардна ціпа активу X — 104 гр. од. Тоді інвестор продає форвард (тобто укладає форвардну угоду па поставку активу X через 3 міс. за ціною 104 гр . од.), позичає 100 гр. од. на три місяці під 16% річних і купує фінансовий актив X за ринковою ціною 100 гр. од.

Через три місяці іпвсетор отримує дохід за активом у розмірі 5 гр. од., здійснює поставку активу, отримує за цс 104 гр. од. і повертає основну суму боргу в розмірі 100 гр. од. та проценти в розмірі 100 • 0,16 : 4 = 4гр. од.

Результатом реалізації такої стратегії є прибуток у розмірі 5 гр. од. Дійсно, доходи та витрати за проведеною операцією становлять:

Отже, Прибуток = Доходи - Витрати = 209 - 204 = 5 гр. од.

II. Припустимо, що форвардна ціна активу X — 93 гр. од. Інвестор позичає у брокера па 3 міс. (як правило, позичка безпроцентна) актив Х_У продає його па ринку за 100 гр. од. і інвестує кошти па 3 міс. під 16% річних. Одночасно він купує форвард (тобто укладає форвардну угоду на купівлю активу X через 3 міс. за ціною 93 гр. од.).

Через 3 міс. інвестор отримує інвестовані 100 гр. од. та дохід за ними: 100 • 0,16 : 4 = 4 гр. од. Згідно з форвардним контрактом ку-

пус актив за ціною 93 гр. од. і повертає брокеру актив X та дохід за активом X. Доходи і витрати від реалізації такої стратегії становлять:

Отже! Прибуток = Доходи - Витрати ~ 204 — 198 = 6 гр. од.

Перша та друга стратегії є прикладами арбітражних стратегій, які дають змогу отримати арбітражний прибуток у випадках, коли форвардна ціна нижча чи вища від теоретичної форвардної ціни.

Теоретичну форвардну ціпу визначимо, прирівнявши прибуток, отриманий у результаті реалізації першої чи другої стратегій, до нуля. Нехай Ц_е — ціна спот активу Х г , г_{ — відповідно ставки з фінансування та інвестування; Ф — форвардна ціна активу X; k_t — дохідність активу X, виражена у процентах до ринкової ціни. Тоді доходи та витрати згідно зі стратегіями І та II матимуть такий вигляд:

Процентні ставки в даному випадку виражені не в річних процентах, а за квартал. Відповідно до наведеного вище прикладу г_ф = = г, = 16 : 4 = 4%, л_а = 5%, оскільки на інвестовані в актив X кошти за квартал сплачують 5 гр. од. доходу. Якщо прийняти г = г_х - г, отримаємо вираз для теоретичної форвардної ціни

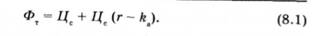
Це теоретична ціпа для контрактів, які не переоцінюються наприкінці дня, як біржові ф'ючерсні контракти. Якщо вважати процентну ставку з фінансування вищою від ставки з інвестування (^гф ^{> Г})*Щ° більше відповідає дійсності, отримаємо верхню та нижню межі форвардних цін:

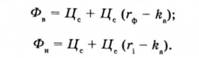
Теоретична форвардна ціна перебуває в інтервалі Ф , Ф , тобто Ф_я< Ф_г< Ф_ш. Врахування коштів на відкриття та закриття позиції розширюють межі Ф_н, Ф_п.

Різницю між вартістю фінансування та дохідністю активу г - k називають чистою вартістю фінансування (net financing cost, або cost of carry). При наближенні дати поставки форвардна ціна наближається до ціни па грошовому ринку, і в день поставки ці ціпи збігаються, тобто Ф_т = Ц_е, оскільки вартість фінансування і дохід за активом дорівнюють нулю (г = Л ).

Припустимо, що за період до дати поставки за активом X не сплачується дохід, тобто k, = 0. Тоді вираз (8.1) матиме вигляд:

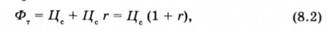
аналогічний формулі теперішньої та майбутньої вартості

Це означає, що ціна спот є дисконтованою величиною майбутньої ціпи активу X, яку інвестор погоджується заплатити на дату поставки (у нашому прикладі через три місяці). Якщо позначити через г річну процентну ставку, що сплачується т раз на рік, вираз (8.2) матиме вигляд:

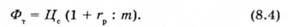
Поряд з процентними ставками, що нараховуються т раз на рік, використовують поняття неперервної процентної ставки, тобто ставки, що нараховується неперервно, — г_н. Дискретна процентна ставка, що нараховується т раз на рік г з достатнім ступенем точності при г, що не досягає великих значень, може бути виражена через процентну ставку г :

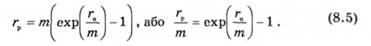
У цьому разі неперервна процентна ставка г_н називається ставкою, еквівалентною г . Використовуючи неперервну процентну ставку, зв'язок між теоретичною форвардною ціною і ціною спот активу можна виразити так:

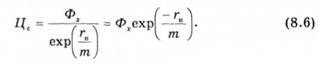
За такою самою формулою може бути розрахована і нарощена сума від інвестування під неперервну процентпу ставку г_н:

Отже, теоретична форвардна ціна отримується з умови рівності результатів таких двох стратегій.

І. Купити актив у даний момент за ціною спот.

П. Інвестувати кошти, що дорівнюють приведеній вартості ціни поставки па період до дати поставки, а потім купити актив згідно з форвардним контрактом.

Якщо за активом за період до дати поставки сплачується дохід, теоретична форвардна ціна визначається з рівності результатів таких двох стратегій.

I. Купити актив у даний момент і отримати дохід за ним.

II. Інвестувати кошти, що дорівнюють приведеній вартості ціни поставки і доходу за активом, а потім придбати актив згідно з форвардним контрактом.

Визначимо, якою буде ціна форвардного контракту, якщо через місяць власник контракту продасть його іншому інвестору.

Для зручності використаємо неперервну процентну ставку і вираз (8.6), що визначає теоретичну форвардну ціну.

Як і в попередньому прикладі, ціна спот активу X дорівнює 100 гр. од. Неперервна процентна ставка для інвестування чи фінансування г_я — 16% річних. Дата поставки за форвардним контрактом — через три місяці. Дохід за активом X протягом періоду не сплачується. Згідно з (8.6) теоретична форвардна ціна

Ф_ж = Ц.ежр^Ч = 100 ехр^~ ^ = 104,08 гр. од. (8.8)

(т = 4, оскільки термін контракту три місяці).

Якщо форвардна ціна вища або нижча від теоретичної, укладаються відповідні арбітражні угоди.

I. Якщо форвардна ціна нижча за теоретичну (наприклад, Ф = = 102 гр. од.), позичається фінансовий актив у брокера, продається на ринку за 100 гр. од., а кошти інвестуються на 3 міс. під 16% річних. Одночасно купується форвард, за яким через 3 міс. буде куплено актив за 102 гр. од. Арбітражний прибуток від реалізації цієї стратегії дорівнює різниці між доходом від інвестицій (нарощена сума визначається за формулою (8.7) і дорівнює 104,08 гр. од.) та витратами на купівлю активу згідно з форвардним контрактом за ціною 102 гр. од. Прибуток дорівнює 104,08 - 102 = 2,08 гр. од.

II. Якщо форвардна ціна вища за теоретичну і дорівнює 107 гр. од., продається форвардний контракт і купується актив за позичені під 16% кошти. Через 3 міс. продається згідно з форвардним контрактом актив X за 107 гр. од. і віддається борг у розмірі 104,08 гр. од. Арбітражний прибуток від реалізації цієї стратегії: 107-104,08 = = 2,92 гр. од.

Припустимо, що через 1 міс, коли ціна спот активу становитиме 108 гр. од., власник контракту захоче продати контракт іншому інвестору. Ціна поставки, зафіксована в контракті, дорівнює 104,08 гр. од. Якою буде ціна форвардного контракту?

Новий власник повинен буде через 2 міс. за цим форвардним контрактом сплатити за актив 104,08 гр. од. На даний момент це еквівалентно сумі

104,08 : ехр(0,16 : 6) = 101,34 гр. од.

Отже:

I. Інвестувавши сьогодні 101,34 гр. од., через 2 міс. можна отримати 104,08 гр. од. і сплатити за актив X згідно з форвардним контрактом або:

II. Купити актив X за ціною спот 103 гр. од. на ринку.

Ціну форвардного контракту ф можна обчислити виходячи з умови рівності результатів першої та другої стратегій, а саме:

101,34 + ф = 103 гр. од.

Звідси ф = 1,66 гр. од., або в загальному вигляді:

0 = Д_в-Ц_п.ехрГ^1. (8.9)

Якщо врахувати вираз (8.6), отримаємо

ф = (ф - д_п). ехрГ^Ч. (8.10)

Тобто ціпа форвардного контракту дорівнює різниці між ціною спот Ц_с і приведеною вартістю ціни поставки Ц ,або дорівпює приведеній вартості різниці між поточною форвардною ціною Ф і ціною поставки Ц .

Виходячи з викладеного, можна зробити такі висновки.

1. При оцінці форвардної ціни активу слід виходити з рівності результатів від купівлі форварду на актив або самого активу.

2. Якщо форвардна ціна вища або нижча від теоретичної форвардної ціни, можна здійснити арбітражну форвардну угоду. Якщо форвардна ціпа вища за теоретичну, продається форвард і купується актив. Якщо форвардна ціна нижча за теоретичну, купується форвард і продається актив. В обох випадках отримується арбітражний прибуток.

3. Якщо форвард продається на вторинному ринку, він має ціну, що відображає різницю між ціною поставки і поточною форвардною ціною.