Для сучасної промисловості властива широка, постійно зростаюча номенклатура вироблених товарів. Розвиток економіки призводить до подальшого збільшення типів і типорозмірів виробів, що пов'язано зі створенням нових видів продукції та потребою у широкому розвитку механізації й автоматизації виробництва.
У ряді випадків має місце випуск надмірно великої номенклатури товарів, що схожі за призначенням і незначною мірою відрізняються конструктивним виконанням і розмірами. Це знижує серійність виробництва продукції, ускладнює уніфікацію виробів, гальмує розвиток спеціалізації виробництва, подовжує термін опанування новою технікою, збільшує виробничі витрати, порушує номенклатуру запасних частин, здорожує ремонт, підвищує вартість обслуговування при експлуатації та наданні послуг. Тенденція щодо збільшення кількості типів і типорозмірів виробів виникає через неузгодженість різних виробництв та дослідних організацій, що здійснюють розробку схожих товарів. Упорядкування номенклатури і кількості типорозмірів виробів є одним із найважливіших завдань стандартизації.
Основою для раціонального скорочення номенклатури і кількості типорозмірів вироблених товарів є розробка параметричних НД — одного із важливих напрямів стандартизації. Ці НД установлюють параметри і розміри найбільш раціональних видів, типів і типорозмірів машин, приладів, обладнання тощо. Створення та використання товарів буде найбільш успішним у тому випадку, коли їх параметри і розміри будуть погоджені між собою. Узгодження різних параметрів і розмірів методом параметричної стандартизації дає змогу пов'язати між собою різні галузі промисловості, що приведе до великого економічного ефекту в масштабах усієї економіки країни.
Сутність параметричної стандартизації полягає у тому, що параметри і розміри виробів установлюють не довільно, а дотримуються визначених, чітко обґрунтованих рядів переважних чисел, що підпорядковані певній математичній закономірності. Переважними називають числа, які рекомендовано вибирати переважно перед усіма іншими для визначення величин параметрів і розмірів при створенні виробів, конструюванні, розрахунках, стандартизації та уніфікації.
Приклади використання переважних чисел зустрічаються всюди — це розміри одягу і взуття, довжина цвяхів, номінальні значення маси гир, потужність електричних машин тощо. Результатом використання саме переважних чисел є таке узгодження параметрів і розмірів, у тому числі й у міжгалузевому відношенні, яке забезпечує взаємозамінність деталей, створення гнучких виробничих систем, автоматизацію і механізацію виробничих процесів, підвищення якості продукції та продуктивності праці. Переважні числа та їх ряди є основою упорядкування вибору величин і градації параметрів усіх виробничих процесів, обладнання, пристроїв, інструментів, матеріалів, напівфабрикатів, транспортних засобів тощо.
Теоретичною базою сучасної стандартизації є система переважних чисел. Сутність цієї системи полягає в тому, що будь-які параметри виробу (продуктивність, число обертів, швидкість, потужність, тиск, розміри) керуються певним науково обґрунтованим рядом переважних чисел, тоді виріб буде узгоджуваний з іншими видами продукції: електродвигуни — з технологічним обладнанням, вантажопідйомними пристроями; вантажопідйомні пристрої — з вантажними машинами; вантажні машини — з транспортною тарою; транспортна тара — зі споживчою тарою і т.п.
Ряди переважних чисел мають відповідати таким вимогам:
— являти собою раціональну систему градацій, що відповідає потребам виготовлення та експлуатації виробів;
— бути нескінченними, як у бік малих, так і великих чисел, допускати збільшення і зменшення їх значення;
— включати всі послідовні десятикратні чи дробові значення кожного числа ряду й одиницю;
— бути простими, щоб їх було легко запам'ятовувати.
При встановленні розмірів виробів широке застосування знайшли ряди чисел, побудовані на основі арифметичної чи геометричної прогресії.
Найпростіші ряди переважних чисел будуються на основі арифметичної прогресії — послідовності чисел, в якій різниця між наступним і попереднім членами ряду залишається постійною, тобто:
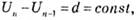
де U — значення членів ряду, що стоять поряд; d — різниця (інтервал) значень між двома суміжними членами ряду; n — порядковий номер члена ряду.
Будь-який член арифметичної прогресії можна обчислити за формулою:
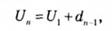
де U1 — перший член арифметичної прогресії.
Графічно арифметична прогресія зображена прямою лінією (рис. 1.3).
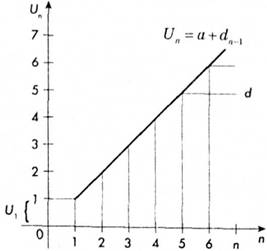
Рис. 1.3. Графік арифметичної прогресії
Позитивним у рядах арифметичної прогресії є те, що вони прості, не потребують округлення чисел. Але суттєвим недоліком є відносна нерівномірність. При сталій абсолютній різниці між членами ряду відносна нерівномірність різко зменшується. Так, відносна різниця між членами арифметичного ряду 1, 2 ... 9 для чисел 1 і 2 складає 100 %, а для чисел 9—10 — усього 11 %. Якщо зміну відносної різниці для членів цього ряду зобразити графічно, то отримаємо залежність, за якою при зростанні абсолютних значень членів арифметичного ряду відносна різниця зменшується (рис. 1.4).
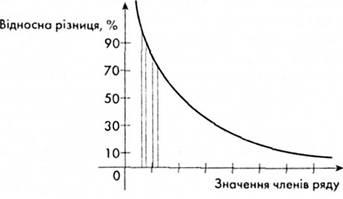
Рис. 1.4. Залежність відносної різниці членів арифметичного ряду від їхнього місця у ряді
Ряди переважних чисел, основані на арифметичній прогресії, мало використовуються у параметричних стандартах. Вони застосовуються, наприклад, у стандартах розмірів взуття, діаметрів підшипників коливання, метричних різьблень, модулів зубчастих колес тощо.
Найбільш придатні для стандартизації параметрів і розмірів геометричні ряди чисел, які являють собою геометричну прогресію. Геометрична прогресія — це ряд чисел, в якому кожне наступне число отримується множенням попереднього на одне й те саме число, яке називається знаменником прогресії:
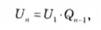
де U1 — перший член прогресії; Qn-1 — знаменник прогресії; п — порядковий номер взятого члена прогресії.
Ряд геометричної прогресії являє собою Q; Qх; Qх2; Qх3... Qхn-1 або 1, 2, 4, 8, 16, 32, 64..., де знаменником прогресії буде 2. Графік геометричної прогресії зображено на рис, 1.5.
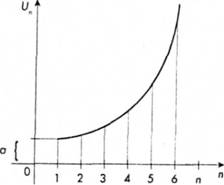
Рис. 1.5. Графік геометричної прогресії
Геометрична прогресія має ряд корисних властивостей.
1. Відносна різниця між будь-якими сусідніми членами ряду постійна. Кожний член прогресії більший за попередній на 100%.
2. Добуток чи частка будь-яких членів прогресії є членом цієї прогресії. Ця властивість використовується при пов'язуванні між собою параметрів і розмірів товарів, що підлягають стандартизації у межах одного ряду переважних чисел.
Геометричні прогресії дають змогу погоджувати між собою параметри і розміри, які пов'язані не тільки лінійною, а й квадратичною, кубічною та іншими залежностями. Ще в Давній Римській імперії діаметри колес водопроводів були вибрані згідно з геометричною прогресією. У Франції в 1805 р. розміри типографського шрифту було встановлено також відповідно до геометричної прогресії.
Історія утворення рядів переважних чисел пов'язана з ім'ям офіцера французького інженерного корпусу Шарля Ренара, який у 1877—1879 рр. заклав наукові основи використання переважних чисел для конструювання. Ураховуючи перевагу геометричної прогресії, Ренар прийняв за основу довжину і побудував ряд, припустивши, що такий знаменник прогресії забезпечує десятикратне збільшення кожного члена ряду, тобто aQ5 = 10a, звідки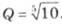 
. Таким чином, Ренар одержав числовий ряд: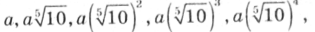 
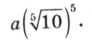
При обчислюванні з точністю до п'ятої цифри цей ряд має такий вигляд: la; 1,5849a; 2,5119a; 3,9811a; 6,3096a; 10a. Для практичного користування ці значення були замінені більш зручними округленими величинами. При цьому а визначено числом 10/?, де k — будь-яке ціле додатне чи від'ємне число, а також нуль. В останньому випадку при h = 0 отримуємо ряд Ренара R5: 1; 1,6; 2,5; 4; 6,3; 10, який може бути продовжений в обох напрямках. Членами ряду переважних чисел є округлені значення членів ряду геометричної прогресії в інтервалі 1...10, які застосовуються при встановленні градацій геометричних параметрів.
У 1953 р. Міжнародна організація зі стандартизації (ISO) прийняла Міжнародні рекомендації щодо переважних чисел ISO/P3, які стали основою для розробки параметричних стандартів у багатьох країнах світу. До рекомендацій, крім ряду Я5, увійшли ряди Я10; R20; #40, які також отримали назву рядів Ренара. Існують ще два додаткових ряди — RS0 і Л160, які використовують тільки в окремих, технічно обґрунтованих випадках.
У 1955 р. прийнята рекомендація ISO/ Р17 "Керівництво з використання переважних чисел і рядів переважних чисел". Відповідно в Україні діє ГОСТ 8032.
Параметри і розміри виробів, які випускають серійно, установлюють відповідно до основних рядів переважних чисел. Але допускається використання похідних рядів, які отримують із основних шляхом відбору 2-, 3-, 4-го чи n-го члена основного чи додаткового ряду. Наприклад, R5/2 — похідний ряд, отриманий із кожного 2-го члена основного ряду R5. Похідні ряди використовують тоді, коли жоден з основних не задовольняє заданим вимогам.
Уведення в усіх галузях промисловості єдиного порядку під час переходу від одних числових значень параметрів і розмірів до інших зменшує кількість типорозмірів, забезпечує економію початкових матеріалів, дає змогу погодити і пов'язати між собою різні види виробів, матеріалів, напівфабрикатів, транспортних засобів, виробниче устаткування тощо.
Розробку параметричних НД на об'єкти стандартизації здійснюють у такій послідовності:
— вибір номенклатури параметрів і розмірів;
— вибір діапазону параметричного ряду;
— вибір градації параметричного ряду.
Параметричний ряд — це сукупність числових значень параметрів і розмірів, які побудовані в певному діапазоні на основі прийнятої системи градацій. Для визначення параметричного ряду слід враховувати його дві характеристики: діапазон ряду та градацію. Діапазон ряду — це інтервал, обмежений крайніми значеннями членів ряду. Градацією параметричного ряду називають математичну закономірність, що визначає характер інтервалів між членами ряду в певному діапазоні. Вибір оптимальної градації параметричного ряду зводиться до знаходження такого ряду переважних чисел, який найбільшим чином відповідав би вимогам економіки країни.
Використання системи переважних чисел з різними рядами допускає можливість їх комбінування. Більшість параметричних рядів, включених до чинних параметричних НД, побудована на основі ряду RIO. Це дає підставу вважати, що ряд RIO є нині найбільш доцільним для побудови параметричних рядів на машини та устаткування.
Згідно з характерними властивостями товарів розрізняють найбільш важливі параметри продукції:
— розмірні параметри (розмір одягу та взуття, місткість посуду);
— параметри ваги (маса окремих видів спортивного інвентарю);
— параметри, які характеризують продуктивність машин і приладів (продуктивність вентиляторів, швидкість руху транспортних засобів);
— енергетичні параметри (потужність двигуна).
Контрольні запитання
1. Схарактеризуйте принципи, методи та форми стандартизації.
2. Що є основою методу уніфікації? На яких рівнях здійснюється робота з уніфікації?
3. Які розрізняють види взаємозамінності? Дайте їм характеристику.
4. Схарактеризуйте види спеціалізації.
5. У чому виявляється сутність комплексної та випереджальної стандартизації?
6. З якою метою розроблені ряди переважних чисел?
7. Перелічіть основні властивості переважних чисел.
8. Що являють собою ряди переважних чисел?
9. Що є основним критерієм при визначенні градації параметричного ряду та при розробленні параметричних НД?
10. У якій послідовності здійснюється розроблення параметричних НД?
3.1. Основні положення Національної стандартизації України
3.2. Органи стандартизації та їхні функції
3.3. Види нормативних документів
3.4 Порядок розроблення, затвердження то впровадження нормативних документів
3.5. Порядок перегляду, зміни та скасування нормативних документів
3.6. Державний нагляд за додержанням нормативних документів
3.7. Інформаційне забезпечення стандартизації
Розділ 4. Міжгалузеві системи стандартизації
4.1. Система конструкторської документації