Франчайзинг - Кузьмін О.Є. - Контрольні запитання

Встановивши розмір франчайзингової винагороди, франчайзер стикається з необхідністю прийняття рішення щодо способу и стягнення з франчайзі. Під способом стягнення франчайзингової винагороди розуміють структуру винагороди, тобто відносні частки першопочаткового внеску та періодичних відрахувань в її складі, та форму здійснення періодичних франчайзингових платежів.

Прийняття франчайзером рішення щодо способу стягнення винагороди відбувається під впливом низки факторів, зокрема:

– стратегічних інтересів франчайзера;

– схильності франчайзера до ризику;

– фінансових можливостей потенційного франчайзі – платника винагороди;

– прогнозованих значень показників, що характеризують результати діяльності франчайзингового підприємства, та ймовірності виправдання таких прогнозів;

– домовленостей сторін франчайзингового договору тощо.

Очевидним є те, що франчайзери, які зацікавлені в швидкому накопиченні капіталу за рахунок продажу франчайзингових пакетів (наприклад, з метою проведення широкомасштабних науково-дослідних робіт, подальшого розширення власної діяльності тощо), наполягатимуть на високій частці першопочаткового платежу в структурі франчайзингової винагороди. Високій питомій вазі першопочаткового внеску, а також формам фіксованого нарахування періодичних платежів нададуть перевагу несхильні до ризику франчайзери. У той час як для готових йти на ризик власників франшиз, за умови існування виправданої ймовірності досягнення підприємством франчайзі високих результатів діяльності, привабливими будуть висока відносна частка періодичних відрахувань у складі франчайзингової винагороди та форми комісійного їх нарахування. Фран- чайзери, зацікавлені у підписанні франчайзингового договору з конкретним суб'єктом господарювання, прийматимуть рішення щодо способу стягнення франчайзингової винагороди з урахуванням фінансових можливостей та інтересів останнього.

Таким чином, існування різних станів перерахованих вище факторів зумовлює використання франчайзерами різних способів стягнення винагороди зі своїх франчайзі.

Водночас, практика функціонування франчайзингових систем показує, що найбільшого поширення (76 % франчайзерів [149]) набуло стягнення франчайзингової винагороди у вигляді різних комбінацій першопочаткового внеску та періодичних відрахувань із використанням такої форми комісійного нарахування періодичних платежів, яка передбачає їх встановлення у вигляді відсотка від обсягів реалізації продукції франчайзингового підприємства. Такий спосіб стягнення франчайзингової винагороди представимо у вигляді формули:

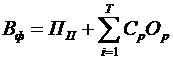, (3.7)

де 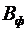– сукупний розмір франчайзингової винагороди, грн; 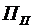– першопочатковий платіж, грн; 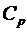– ставка періодичних франчайзингових платежів (роялті), коефіцієнт; 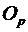– обсяг реалізації франчайзингового підприємства у f-му році, грн; Т – термін дії франчайзингового договору, роки.

Ставка періодичних франчайзингових платежів 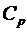встановлюється з урахуванням того, щоб у випадку, якщо обсяги реалізації франчайзингового підприємства відповідатимуть прогнозам франчайзера, загальна сума винагороди, яку отримає франчайзер, відповідала б його очікуванням.

Однак прогнози франчайзера можуть не виправдатись на практиці, що зумовить відхилення реально отриманого ним розміру винагороди від очікуваного. При цьому величина такого відхилення значною мірою залежатиме від обраної франчайзером структури винагороди. Так, встановлюючи достатньо високу відносну частку першопочаткового платежу в структурі франчайзингової винагороди, франчайзер уникає ризику недоотримання значної суми очікуваної винагороди у випадку, якщо фактичні обсяги реалізації франчайзингового підприємства будуть суттєво нижчими за їх прогнозовані значення. Але при цьому франчайзер втрачає можливість отримання додаткових доходів від діяльності свого франчайзі в разі, якщо товарообороти останнього значно перевищать сподівані їх значення в результаті формування сприятливого ринкового середовища. Така можливість залишається у франчайзера у випадку встановлення ним високої ставки роялті за рахунок зменшення відносної частки першопочаткового внеску в структурі винагороди. Проте таке рішення франчайзера породжує вже згадуваний ризик недоотримання суттєвої величини очікуваної винагороди в разі несприятливої ринкової кон'юнктури чи неуспішної діяльності франчайзингового підприємства з вини франчайзі.

Таким чином, процес прийняття франчайзером оптимального рішення щодо структури франчайзингової винагороди у випадку, якщо він має намір проводити нарахування періодичних платежів у вигляді відсотка від обсягів реалізації франчайзингового підприємства, повинен базуватися на ретельному математичному аналізі та вимагає відповідного методичного забезпечення.

Прийняття управлінських рішень в економіці проводиться в умовах існування одного з таких "станів знань" суб'єкта прийняття рішення, як визначеність, ризик та невизначеність.

Прийняття рішення в умовах визначеності передбачає володіння менеджером вичерпною та достовірною інформацією щодо результатів кожного з альтернативних варіантів рішення.

В умовах ризику суб'єкт прийняття рішення володіє знаннями щодо одного або кількох результатів кожної з альтернатив, а також щодо ймовірності настання кожного з таких результатів.

У випадку, коли таку ймовірність об'єктивно оцінити неможливо або вона не має змісту, говорять про прийняття рішення в умовах невизначеності.

Існує низка методів і моделей прийняття оптимальних рішень в умовах визначеності, ризику та невизначеності. З метою вибору тих із них, які доцільно використати у процесі визначення франчайзером оптимальної структури франчайзингової винагороди, необхідно встановити "стан знань" франчайзера як суб'єкта прийняття рішення.

Рішення франчайзера щодо структури франчайзингової винагороди має низку альтернатив, які полягають у різних комбінаціях першопочаткового платежу та періодичних відрахувань. При цьому франчайзер не володіє інформацією щодо результату прийняття кожного з альтернативних варіантів рішення, тобто щодо розміру сукупної франчайзингової винагороди, що буде ним отримана у випадку вибору кожної з альтернатив. Це зумовлюється відсутністю достовірної інформації про майбутні обсяги реалізації підприємства франчайзі, які безпосередньо впливають на абсолютну суму періодичних платежів. Водночас, на основі емпіричних даних (досвіду функціонування підприємств системи франчайзера або інших підприємств відповідного профілю та розміру), тенденцій розвитку ринку, місця продукції з торговельною маркою франчайзера на ринку та інших інформаційних даних франчайзер може встановити об'єктивний розподіл ймовірності можливих обсягів реалізації підприємства франчайзі, тобто ймовірність настання кожного з можливих результатів альтернативних варіантів рішення щодо структури франчайзингової винагороди.

Отже, рішення про структуру франчайзингової винагороди приймається франчайзером в умовах ризику.

Правилам прийняття рішень в умовах ризику присвячено низку наукових концепцій. Серед них доцільно виокремити стохастичне програмування, теорії керованих випадкових процесів, нечітких множин, ігор, статистичних рішень тощо, котрі з системних позицій об'єднали класичні ймовірнісні методи з методами і моделями оптимізації складних систем, до яких належить економіка. Досягнуті результати дали змогу розпочати глибоке вивчення проблем економічної (господарської) діяльності з урахуванням ризику і розбудови теорії керування економічною стійкістю, надійністю, маневреністю [38].

Найбільш відомою, достатньо дослідженою та широко застосованою в теорії та на практиці концепцією прийняття рішень в умовах ризику є теорія ігор [38]. З огляду на це, розглянемо методичні рекомендації щодо прийняття франчайзером оптимального рішення стосовно структури франчайзингової винагороди, розроблені із використанням положень згаданої теорії.

Варто зауважити, що теорія ігор і статистичних рішень є широкою галуззю знань і охоплює правила прийняття рішень не лише в умовах ризику, айв умовах невизначеності, що вимагає уважного підходу до вибору критеріїв прийняття рішення в процесі побудови теоретико-ігрових моделей.

За визначенням М. Воробйова, теорія гри – це теорія математичних моделей прийняття рішень в умовах невизначеності, коли суб'єкт, який приймає рішення ("гравець"), має в своєму розпорядженні інформацію лише про множину можливих ситуацій, в одній з яких він насправді знаходиться, про множину рішень ("стратегій"), які він може приймати, та про кількісну міру того "виграшу", який він міг би отримати, обравши у певній ситуації конкретну стратегію [20].

У нашому випадку суб'єктом прийняття рішень є франчайзер; множиною ситуацій, в яких він може опинитися, – множина можливих обсягів реалізації продукції підприємства його франчайзі; множиною рішень, які він може приймати, – множина можливих структур франчайзингової винагороди; кількісною мірою "виграшу", який він може отримати, прийнявши конкретне рішення в певній ситуації, – загальна сума отримуваної ним франчайзингової винагороди.

Щоб описати будь-яку гру, необхідно спочатку виявити її учасників. Зважаючи на те, що учасниками гри (гравцями) можуть бути окремі особи, підприємницькі структури, а також різні явища й об'єкти природи, завдання пошуку оптимальної структури франчайзингової винагороди можна звести до гри франчайзера та економічного середовища, стан якого безпосередньо впливає на обсяги реалізації франчайзингового підприємства і, як наслідок, на абсолютну величину періодичних відрахувань, що підлягають сплаті на користь франчайзера.

У наведених далі методичних рекомендаціях з визначення оптимальної структури франчайзингової винагороди, використано пропоновані у роботах В. Вітлінського, П. Верченка, А. Сігала, Я. Наконечного схему моделювання процесу прийняття раціонального рішення в умовах ризику та невизначеності, а також послідовність побудови теоретико-ігрових моделей.

Основними складовими схеми гри з економічним середовищем є [18; 39]:

1) перший гравець – суб'єкт прийняття рішення, вибір стратегії поведінки якого базується на множині S = (s₁,..., s_m) рішень (чистих стратегій), одне з яких йому необхідно прийняти;

2) другий гравець – економічне середовище, яке може знаходитись в одному з п попарно несумісних станів q_j, які утворюють множину q = (q₁, ..., q_n), і один з яких обов'язково настане;

3) відсутність у суб'єкта прийняття рішення апріорної інформації про те, в якому зі своїх станів знаходитиметься економічне середовище (яке рішення прийме другий гравець);

4) точне знання суб'єктом прийняття рішення платіжної матриці (функціонала оцінювання) F = (f_kj: k = 1,..., m; j = 1, ..., n), елемент f_kj, якої є кількісною оцінкою вигоди суб'єкта прийняття рішення у разі вибору ним стратегії s_k та реалізації стану економічного середовища q _j(k = 1,..., m; j = 1, ..., n).

Основними етапами побудови теоретико-ігрової моделі є [18; 38]:

1) формування множин рішень першого та другого гравців, тобто перелік чистих стратегій суб'єкта прийняття рішення і станів економічного середовища;

2) визначення та формалізація основних показників ефективності та корисності, побудова платіжної матриці;

3) визначення (ідентифікація) наявної інформаційної ситуації, яка характеризує поведінку економічного середовища;

4) вибір критерію прийняття рішення з множини критеріїв, характерних для ідентифікованої інформаційної ситуації;

5) прийняття згідно з вибраним критерієм рішення з сукупності чистих або змішаних стратегій, якщо використання останніх можливе.

Застосовуючи загальноприйняті в концепції теорії гри та статистичних рішень термінологію і математичні позначення, вищерозглянуті схему моделювання процесу прийняття оптимального рішення та послідовність побудови теоретико-ігрових моделей, сформулюємо основу ігрової моделі вибору франчайзером оптимальної структури франчайзингової винагороди таким чином:

– маємо парну гру, тобто гру, в якій беруть участь двоє гравців:

– перший гравець – франчайзер (він же суб'єкт прийняття рішення);

– другий гравець – економічне середовище. Під економічним середовищем розуміють сукупність невизначених чинників, які впливають на ефективність рішення, що приймається [18];

– множина рішень першого гравця, тобто перелік чистих стратегій франчайзера як суб'єкта прийняття рішення, має вигляд:

S = (s₁; s₂), (3.8)

де s₁ – перша чиста стратегія франчайзера, яка передбачає стягнення всього розміру франчайзингової винагороди у вигляді першопочаткового платежу; s₂ – друга чиста стратегія франчайзера, яка передбачає стягнення всього розміру франчайзингової винагороди у вигляді періодичних франчайзингових платежів;

– множина рішень другого гравця, тобто перелік чистих стратегій економічного середовища, має вигляд:

q = (q₁, ..., q_n) (3.9)

де q₁, ..., q_n – чисті стратегії економічного середовища (обсяги реалізації франчайзингового підприємства впродовж усього терміну дії франчайзингового договору).

Чисті стратегії економічного середовища доцільно формулювати, виходячи з імовірних меж коливань обсягів реалізації франчайзингового підприємства. Для спрощення подальших розрахунків пропонується обирати 7–10 значень можливих обсягів реалізації франчайзингового підприємства, що знаходяться у встановлених межах;

– ймовірності реалізації економічним середовищем своїх чистих стратегій (ймовірності реалізації франчайзинговим підприємством визначених обсягів продукції) задаються множиною:

Q (q₁, …, q_n) (3.10)

де q₁, …, q_n – ймовірності реалізації відповідних станів економічного середовища q₁, ..., q_n.

При цьому з позиції теорії ймовірностей повинні виконуватись такі умови:

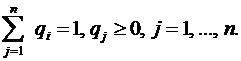(3.11)

Існує два основних підходи до об'єктивного оцінювання ймовірності [54; 104]: метод апріорі та метод апостеріорі.

Метод апріорі передбачає дедуктивне (тобто без експериментування та врахування минулого досвіду) визначення ймовірностей настання тих чи інших подій, а отже, його використання для встановлення ймовірностей реалізації франчайзинговим підприємством обсягів продукції, що формують множину Q, є недоцільним.

Метод апостеріорі передбачає встановлення ймовірностей шляхом статистичного аналізу емпіричних даних. Його використання дозволить встановити ймовірність реалізації підприємством франчайзі визначених обсягів продукції, виходячи з досвіду функціонування аналогічних за видом діяльності та розміром франчайзингових чи незалежних (за відсутності перших у системі франчайзера) підприємств.

Використання методу апостеріорі передбачає визначення (у відсотках) розподілу частоти настання подій, щодо яких ведеться спостереження, з подальшим його перетворенням у розподіл імовірності настання таких подій.

Важливо зазначити, що отриманий таким чином розподіл імовірності може бути модифікований з метою врахування впливу нових факторів, які можуть мати важливе значення у майбутньому, або з метою коригування впливу минулих факторів, дія яких не продовжуватиметься в майбутньому [104].

У нашому випадку це означатиме, що розподіл імовірності реалізації економічним середовищем кожної зі своїх чистих стратегій, що утворюють множину Q, доцільно формувати з урахуванням не лише емпіричних даних, а й прогнозів щодо майбутніх тенденцій розвитку ринку тощо;

– правила поведінки франчайзера щодо вибору оптимальної стратегії формуються на основі такої платіжної матриці (функціонала оцінювання):

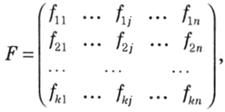
де f_kj – міра ефективності використання франчайзером своєї чистої стратегії S_k, коли економічне середовище знаходиться у стані q_j, іншими словами, загальний розмір франчайзингової винагороди, яку отримає франчайзер, використавши стратегію s_k, у разі, якщо загальний обсяг реалізації франчайзингового підприємства впродовж усього терміну дії франчайзингового договору становитиме q_j.

Перший рядок платіжної матриці формує вектор оцінювання F(s₁) = (f₁₁, …, f_1n), який складається зі значень оцінки ефективності першої чистої стратегії франчайзера в умовах реалізації кожного з визначених станів економічного середовища. Аналогічно другий рядок матриці формує вектор оцінювання F(s₂) = (f₂₂, …, f_2n), який характеризує використання франчайзером своєї другої чистої стратегії.

Зважаючи на те, що в разі вибору франчайзером стратегії s₁, розмір отриманої ним винагороди не залежатиме від обсягів реалізації франчайзингового підприємства, можна записати:

,

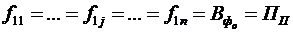де 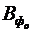– розмір сукупної франчайзингової винагороди, яку очікує отримати франчайзер, грн.

Елементи платіжної матриці, що відповідають стратегії франчайзера s₂, можуть бути розраховані за формулою:

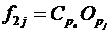, (3.14)

де – ставка роялті, встановлена у розмірі, який дозволить франчайзеру при виправданні його очікувань щодо обсягів реалізації продукції франчайзингового підприємства () отримати очікуваний розмір франчайзингової винагороди (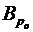) за умов використання ним стратеги s₂, коефіцієнт; 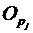– обсяг реалізації продукції франчайзингового підприємства, що відповідає у-й стратегії економічного середовища j - (1, ..., n), за весь термін дії франчайзингового договору, грн.

Сформульована основа ігрової моделі дозволяє перейти до наступного етапу побудови теоретико-ігрової моделі, а саме: ідентифікації наявної інформаційної ситуації, яка характеризує поведінку економічного середовища.

Як уже зазначалося, теорія ігор розкриває правила прийняття рішень в умовах ризику та невизначеності. При цьому конкретна методика прийняття того чи іншого рішення залежатиме від ступеня поінформованості суб'єкта прийняття рішення щодо вибору економічним середовищем одного з можливих його станів.

Певний ступінь градації невизначеності щодо перебування економічного середовища в одному зі своїх можливих станів у момент прийняття рішення суб'єктом керування (гравцем) носить назву інформаційної ситуації (ІС) [38].

Для встановлення інформаційної ситуації, в якій приймається рішення щодо структури франчайзингової винагороди, використаємо класифікатор, згідно з яким виокремлюється сім інформаційних ситуацій [18; 38]:

11 – перша ІС – характеризується заданим розподілом імовірності щодо станів економічного середовища, тобто відомі компоненти вектора Q;

12 – друга ІС – характеризується заданим законом розподілу ймовірностей різних станів економічного середовища, з точністю до невідомих параметрів, які характеризують цей закон розподілу;

13 – третя ІС – характеризується деякою сукупністю обмежень щодо ймовірностей станів економічного середовища;

14 – четверта ІС – характеризується, з одного боку, невідомим розподілом ймовірностей різних станів економічного середовища, а з іншого – відсутністю активної протидії економічного середовища цілям суб'єкта прийняття рішення;

15 – п'ята ІС – характеризується абсолютно протилежними інтересами суб'єкта прийняття рішення та економічного середовища, тобто має місце конфлікт між ними;

16 – шоста ІС – характеризується наявністю деякої інформації щодо розподілу ймовірностей та існуванням протиріч між інтересами суб'єкта прийняття рішення та економічним середовищем, які не обов'язково носять повністю антагоністичний характер;

17 – сьома ІС – характеризується нечіткою (розпливчатою) множиною станів економічного середовища.

Як уже було обґрунтовано вище, франчайзер має змогу встановити об'єктивний розподіл імовірності можливих обсягів реалізації франчайзингового підприємства, а отже, він приймає рішення стосовно структури франчайзингової винагороди в полі першої інформаційної ситуації.

У концепції теорії ігор пропонується кілька критеріїв прийняття рішень у полі першої інформаційної ситуації. Основними з них є [18; 38]:

– критерій Байєса, згідно з яким оптимальним вважається рішення, для якого математичне сподівання відповідного вектора оцінювання досягає найбільшого можливого значення;

– критерії мінливості значень елементів функціонала оцінювання (критерій мінімального сподіваного значення несприятливих відхилень від моди, критерій мінімальної дисперсії, критерій мінімальної семіваріації, критерій мінімального коефіцієнта варіації, критерій мінімального коефіцієнта семіваріації), згідно з якими оптимальним вважається рішення, для якого міра мінливості елементів відповідного вектора оцінювання відносно обраного центру групування (математичного сподівання, моди, медіани тощо) є найменшою.

Для вибору адекватного критерію прийняття франчайзером рішення щодо структури франчайзингової винагороди необхідно оцінити характеристики оптимальної структури винагороди. Очевидно, що оптимальною для франчайзера буде така стратегія щодо структури франчайзингової винагороди, яка здатна забезпечити його найбільшими грошовими надходженнями у вигляді платежів від франчайзі при найменшому рівні ризику. Таким чином, можливі стратегії франчайзера доцільно порівнювати на основі таких двох характеристик:

– сподіваний розмір сукупної франчайзингової винагороди;

– рівень ризику.

Сподіваний розмір сукупної франчайзингової винагороди, яку може отримати франчайзер, використавши певну стратегію, може бути оцінений за допомогою показника математичного сподівання випадкової величини (випадковою величиною у цьому випадку є розмір сукупної франчайзингової винагороди); рівень ризику, що відповідає певній стратегії франчайзера, можна оцінити за допомогою такого параметра, як міра мінливості елементів вектора оцінювання відповідної стратегії відносно центру групування елементів цього вектора (міра мінливості оцінюється за допомогою дисперсії).

Для k-ї чистої стратегії математичне сподівання m_к та дисперсія (якщо центром групування є математичне сподівання) 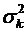розраховуються за формулами [38]:

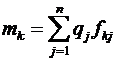; (3.15)

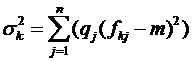. (3.16)

При цьому потрібно знати, що франчайзер може використовувати не тільки свої чисті стратегії, а й змішані.

Змішаною називається стратегія 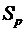суб'єкта прийняття рішення, якій відповідає вектор оцінювання 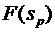, що є лінійною комбінацією векторів оцінювання, які, своєю чергою, відповідають чистим стратегіям [38].

У нашому випадку вектор оцінювання змішаної стратегії франчайзера запишеться у вигляді:

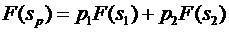, (3.17)

де p₁, р₂ – відносні частки відповідно першопочаткового платежу та періодичних франчайзингових платежів у структурі франчайзингової винагороди, коефіцієнти.

Оскільки за допомогою коефіцієнтів р₁ та р₂ можна описати як будь-яку змішану, так і будь-яку чисту стратегію франчайзера (для першої чистої стратегії франчайзера р₁ = 0, р₂ = 0; для другої чистої стратегії р₁ = 0, р₂ = 1)" то задачу встановлення франчайзером оптимальних відносних часток першопочаткового та періодичних платежів у складі франчайзингової винагороди можна звести до задачі пошуку компонентів вектора розподілу Р = (р₁; р₂) (при цьому p₁+p₂=1, р₁³0, р₂ ³0), тобто до пошуку параметрів оптимальної змішаної стратегії франчайзера.

Для будь-якої змішаної стратегії формули для розрахунку математичного сподівання випадкової величини 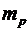та дисперсії випадкової величини 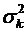мають вигляд [38]:

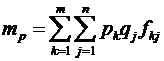; (3.18)

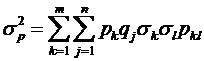, (3.19)

де 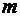– кількість чистих стратегій суб'єкта прийняття рішень; 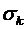(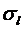) – середньоквадратичне відхилення елементів вектора оцінювання 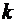-ї (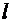-ї) чистої стратегії суб'єкта прийняття рішень відносно математичного сподівання 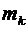(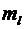) ()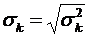; 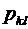– коефіцієнт кореляції (міра щільності зв'язку) між елементами векторів оцінювання 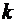-ї та 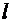-ї чистих стратегій суб'єкта прийняття рішень.

Перетворимо формули (3.18) та (3.19) з урахуванням особливостей аналізованої гри франчайзера з економічним середовищем. Таким чином, зважаючи на те, що:

– ;

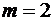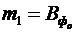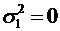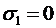– , , , оскільки перша чиста стратегія франчайзера передбачає стягнення всього розміру франчайзингової винагороди у вигляді лише першопочаткового платежу, розмір якого не залежить від стану економічного середовища;

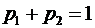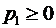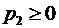– ; , (позначивши 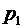через х, отримаємо , );

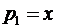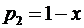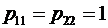– (властивість коефіцієнта кореляції), формули (3.18) та (3.19) для задачі оптимізації структури франчайзингової винагороди можна записати у вигляді:

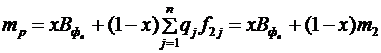, (3.20)

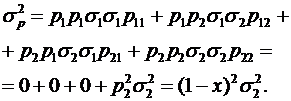(3.21)

Ураховуючи сформульоване вище припущення, що оптимальною вважатимемо стратегію, яка при мінімальному ризику здатна принести франчайзеру максимальну вигоду, економіко-математичну модель вибору франчайзером оптимальної структури франчайзингової винагороди запишемо у вигляді такої двокритеріальної задачі:

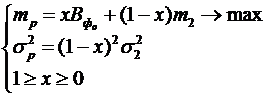(3.22)

Однак запропонована задача не матиме однозначного розв'язку (за винятком випадку, коли математичне сподівання франчайзингової винагороди досягає свого максимального значення для першої чистої стратегії франчайзера, яка характеризується нульовим ризиком), оскільки покращення значення одного критерію може призводити до погіршення значення другого. Оптимальні значення обраних критеріїв оцінки стратегій франчайзера досягатимуться, швидше за все, при різних стратегіях.

Варто зазначити, що всю множину допустимих стратегій можна поділити на дві підмножини: область згоди та область компромісу (рис. 3.4).

В області згоди протиріч між критеріями немає, а тому є можливість щодо поліпшення якості стратегії одночасно згідно з усіма критеріями або, в крайньому разі, без погіршення рівня будь-якого критерію. В області компромісу існують протиріччя між критеріями, а тому поліпшення якості стратегії згідно з одним критерієм призводить до погіршення її якості згідно з іншими. Оптимальна стратегія може належати тільки області компромісу, оскільки в області згоди стратегія може покращуватися згідно з усіма критеріями [38]. Виділення області компромісу дозволяє звузити множину стратегій, серед яких потрібно шукати оптимальну. Наступним, після формулювання задачі (3.22), кроком франчайзера повинно стати встановлення так званого принципу оптимальності, що полягає у визначенні рівня пріоритетності кожного критерію прийняття рішення в процесі визначення оптимальної стратегії.

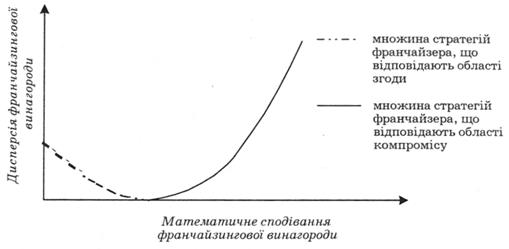
Рис. 3.4. Множина допустимих стратегій франчайзера

Відображати таку пріоритетність у нашому випадку доцільно через присвоєння вагових коефіцієнтів пріоритету для кожного із критеріїв. Сума вагових коефіцієнтів пріоритету обох критеріїв повинна дорівнювати одиниці. Оскільки одним із критеріїв вибору оптимальної стратегії є дисперсія франчайзингової винагороди, яка відображає рівень ризику відповідної стратегії, то, згідно з портфельною теорією [38], ваговий коефіцієнт цього критерію (позначимо його) трактуватиметься як коефіцієнт несхильності франчайзера до ризику. Чим більшим є значення, тим франчайзер є менш готовим йти на ризик, і навпаки. Ваговий коефіцієнт пріоритету математичного сподівання франчайзингової винагороди становитиме (1 - !!!А.).

Присвоєння вагових коефіцієнтів пріоритету кожному з критеріїв вибору оптимальної стратегії дозволяє франчайзеру здійснити такий вибір з урахуванням власної готовності ризикувати задля максимізації отримуваного розміру винагороди.

Основні положення економіко-математичного моделювання [90; 112; 114], теорії корисності [18; 19; 38] та теорії портфеля [18; 19; 38; 49; 100; 128] засвідчують, що сформульована вище двокритеріальна задача визначення оптимальної структури франчайзингової винагороди узгоджується з максимізацією функції корисності франчайзера виду:

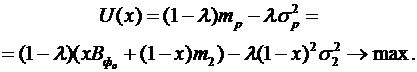(3.23)

Функція 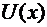досягатиме свого максимуму при такому значенні х, за якого її перша похідна дорівнюватиме нулю.

Знайдене значення 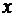(або 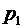), при якому функція (2.9) досягає максимуму, є оптимальною відносною часткою першопочаткового платежу в загальному очікуваному розмірі франчайзингової винагороди. Тобто оптимальна абсолютна сума першопочаткового платежу 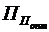, що підлягає сплаті при підписанні франчайзингового договору, визначатиметься за формулою:

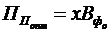. (3.24)

Відповідно значення 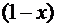(або 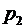) є відносною часткою періодичних франчайзингових платежів у загальному сподіваному розмірі франчайзингової винагороди. При цьому ставка періодичних відрахувань 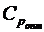, яку франчайзеру доцільно встановити, враховуючи визначену оптимальну структуру франчайзингової винагороди, розраховується таким чином:

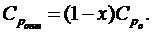(3.25)

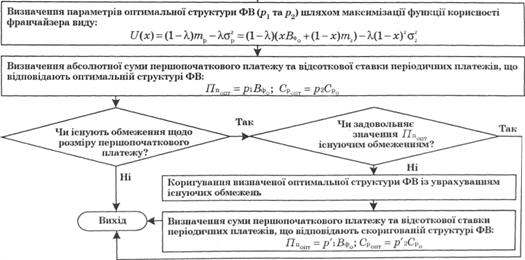
Визначена за допомогою розглянутих методичних рекомендацій оптимальна структура франчайзингової винагороди повинна бути перевірена франчайзером на її відповідність можливим обмеженням щодо розміру першопочаткового внеску. До таких обмежень відносять:

першопочаткового платежу (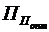), йому доцільно скоригувати встановлену структуру франчайзингової винагороди таким чином:

1) готовність франчайзі одночасно сплатити встановлену суму першопочаткового платежу. У разі, якщо франчайзер зацікавлений укласти франчайзинговий договір з визначеним франчайзі, який, своєю чергою, не спроможний сплатити під час укладання договору визначеного оптимального для франчайзера розміру

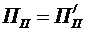, (3.26)

де 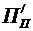– максимальний розмір першопочаткового платежу, який франчайзі готовий сплатити на користь франчайзера, грн.

При цьому ставка періодичних франчайзингових платежів визначатиметься таким чином:

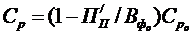; (3.27)

2) наявність законодавчих обмежень щодо розміру першопочаткового внеску. У деяких країнах законодавець встановлює мінімальний розмір першопочаткового платежу, у разі оплати якого правовідносини сторін класифікуватимуться як франчайзингові. Це стосується США, де розмір мінімального першопочаткового платежу становить 500 дол. США. У випадку сплати меншого за розміром платежу правовідносини сторін класифікуватимуться як дистриб'юторські, а не франчайзингові. В Україні кількісні обмеження на першопочатковий франчайзинговий платіж не встановлені.

Якщо визначена за допомогою розглянутих методичних рекомендацій оптимальна структура франчайзингової винагороди передбачає встановлення першопочаткового внеску в розмірі, меншому за мінімально можливий за законодавством, вона може бути скоригована за допомогою використання формул (3.26) і (3.27). У цьому випадку 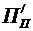трактуватиметься як законодавчо встановлений мінімальний розмір першопочаткового платежу.

Крім наведених обмежень, які унеможливлюють встановлення визначеної за допомогою використання пропонованих методичних рекомендацій структури франчайзингової винагороди, існують деякі інші фактори, що іноді примушують франчайзера коригувати встановлені оптимальні відносні частки першопочаткового платежу та періодичних відрахувань у структурі франчайзингової винагороди.

Так, наприклад, як зазначає Я. Мюррей [80], серед великих франчайзерів вважається неприйнятним встановлення високого розміру першопочаткового внеску. Крім того, франчайзери, що мають серйозні наміри, як правило, прагнуть відразу відділити себе від категорії сумнівних суб'єктів, які заробляють кошти на продажі франшиз, що не мають реальної цінності. Встановлення першопочаткового платежу на надто високому рівні може також перешкоджати залученню нових потенційних франчайзі. У той час як невеликий розмір такого платежу вимагає наявності у франчайзера достатньої суми оборотних коштів для фінансування початкових витрат на створення франчайзингової системи.

Таким чином, встановлення оптимальної структури франчайзингової винагороди є складним процесом балансування, відправною точкою для якого доцільно обрати структуру винагороди, визначену з використанням розглянутих методичних рекомендацій, наочне узагальнення яких представлено у вигляді послідовності оптимізації структури франчайзингової винагороди (рис. 3.5). Така послідовність поетапно розкриває процес оптимізації структури винагороди і призначена для використання франчайзерами під час прийняття ними рішення щодо відносних часток першопочаткового і періодичних платежів у загальній величині франчайзингової винагороди.

Особливістю розглянутих методичних рекомендацій з визначення оптимальної структури франчайзингової винагороди є те, що встановлене з їх використанням оптимальне співвідношення першопочаткового внеску та періодичних платежів у структурі винагороди суттєво залежатиме від присвоєного значення коефіцієнта несхильності франчайзера до ризику.

Зазвичай схильність до ризику розглядається як суб'єктивне ставлення особи, що приймає рішення, до ризику, її здатність ризикувати заради вищих прибутків. Водночас, у праці К. Сіо [104] наголошено на тому, що готовність особи йти на ризик залежить від граничної корисності збитків і додаткових надходжень, що можуть бути нею (або суб'єктом господарювання, на користь якого вона приймає рішення) отримані в результаті вибору тієї чи іншої альтернативи рішення. При цьому гранична корисність залежить не лише від індивідуальних рис характеру особи, що приймає рішення, а й від суттєвості впливу можливих наслідків рішення на цю особу або на діяльність суб'єкта господарювання, на користь якого таке рішення приймається.

Таким чином, коефіцієнт несхильності франчайзера до ризику є об'єктивно-суб'єктивною величиною, тобто величиною, на значення якої впливають як об'єктивні, так і суб'єктивні чинники.

З огляду на це, визначення значення коефіцієнта проводиться шляхом реалізації таких послідовних етапів:

1. Оцінювання об'єктивних чинників. Основними об'єктивними чинниками, вплив яких доцільно враховувати при встановленні коефіцієнта несхильності франчайзера до ризику в процесі оптимізації структури франчайзингової винагороди, є:

– рівень фінансової стійкості франчайзера;

– міра ризиконасиченості рішення щодо структури франчайзингової винагороди;

– рівень стабільності економічної ситуації в державі.

Для оцінювання перерахованих вище чинників побудована модель у вигляді дерева рішень,