Тема 1. Логічний аналіз складних тверджень
ЛЕКЦІЯ 1. Логічні терміни в складних твердженнях
1.1. Прості та складні твердження
Для того щоб з'ясувати, що таке твердження, доцільно порівняти його з розповідним реченням, виявивши між ними відмінні та спільні ознаки. Розповідне речення - це послідовність слів, частиною яких позначено те, про що стверджують, а частиною - те, що стверджують про ці об'єкти. Наприклад, розглянемо таке розповідне речення: Птах летить. Частиною цього речення позначено те, про що стверджують {птах)у а частиною - те, що стверджують (летить), У разі, коли те саме речення буде промовлене (усно чи письмово) словами іншої мови, то це буде вже інше речення. Крім того, зміст цього речення може бути зафіксований жестами або шрифтом Брайля, тобто за допомогою знаків іншої природи.
Однак думка про те, що птах летить, будучи зафіксованою різними знаками, є в усіх цих конкретних проявах речень однаковою. Цей спільний зміст речень різної мови (речень однакового змісту) у традиційній логіці називали терміном судження. Але ми говоритимемо не про думки, тобто не про формулювання цих речень у мисленні людини, а про знаки. Якщо позначимо слово птах символом S, ознаку летить - символом Р, стверджувальну форму цього речення - дефісом, то в символьному вигляді думку птах летить запишемо виразом S-Р (незалежно від того, словами якої конкретної мови позначено об'єкт птах і ознаку летить).
Послідовність символів, якими зафіксоване знання, що містить позначення того, про що стверджують, того, що саме стверджують, і дії стверджування (незалежно від природи і виду конкретних знаків, тобто чи знаками є слова, і якщо слова, то якої мови) називатимемо твердженням. Далі в тексті твердженням будемо називати розповідні речення, мовлені конкретною, наприклад, українською мовою, маючи на увазі, що нас цікавить тільки зміст знаків незалежно від конкретної мови, якій належать ці знаки.
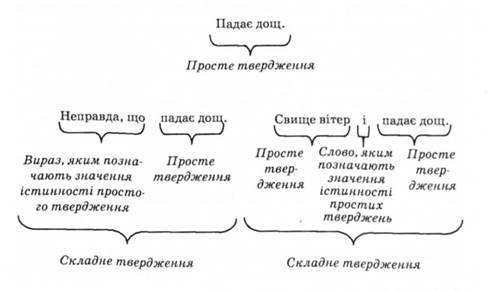
Складне твердження відрізняється від простого тим, що містить знаки, якими позначають значення істинності. Отже, складне твердження - це твердження, яке містить прості твердження-складники (принаймні одне) і логічні терміни, якими позначають значення істинності цих простих тверджень-складників.
1.2. Зміст логічних термінів
Щоб записати зміст логічних термінів, якими позначають значення істинності висловів, уведемо такі позначення. Прості твердження позначатимемо малими літерами латинського алфавіту (р, q, г, в). У разі, якщо аналізований текст чи промова містить багато тверджень, їх можна позначати індексованими літерами латинського алфавіту (р1, р2, р3, ... рn). Якщо твердження істинне, то записуватимемо символ і, якщо ж твердження хибне, - символ х.
Логічні терміни, якими позначають значення істинності тверджень, можна розділити за тим, значення якої кількості тверджень позначають цими термінами. У разі, якщо терміном позначено значення істинності одного твердження, його називають унарним (лат. unus - один). Якщо логічним терміном позначено значення істинності двох висловів, то такий логічний термін називають бінарним (лат. binarius - подвійний).
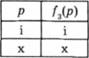
Найуживанішим унарним логічним терміном є "ствердження" (позначимо його f3). Його виражають словами "істинно, що". Цим терміном позначають, що твердження, розміщене після нього, істинне. Оскільки кожне твердження (йдеться про розповідні речення), перед яким відсутні слова "неправда, що" або "хибно, що", людина подає як істинне, то це формулювання (істинно, що) доводилося б промовляти в кожному такому реченні. Через те, що це є нераціонально, то під час мовлення його не вживають, однак розуміють, що в разі, коли нема слів "неправда, що" чи "хибно, що", насправді там має бути слово "істинно", яке вилучили для більш стислого формулювання думки. Водночас кожне твердження (в тому числі кожне складне твердження, тобто таке, яке містить логічні терміни для позначення значення істинності тверджень) подають як істинне - спадною інтонацією (тобто спадною висотою тону) під кінець речення в разі усного мовлення; крапкою - в разі письмового мовлення. Зміст цього логічного терміна фіксують такою таблицею:
З-поміж логічних термінів, якими позначають значення істинності одного твердження, розглянемо також заперечення. Словесно цьому терміну відповідає вираз неправда, що. У працях з логіки є такі символьні позначення цього логічного терміна: р, -*р, -р, ~р, Із цих символів найдоцільніше використовувати перший, оскільки у разі, якщо вислів містить кілька заперечень, його символьний запис за допомогою цього символу дає найкомпактніші вирази, які легше сприймати візуально. Отже, якщо довільне твердження, наприклад, падає дощ, позначимо символом р, то вислів Неправда, що падає дощ записуватимемо виразом р (цей вираз читають не-р або неправда, що р).
Зміст логічного терміна заперечення фіксують такою таблицею:
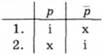
першим рядком цієї таблиці зафіксовано, що в разі істинності вислову р вислів не-р є хибним. Відповідно, другим рядком зафіксовано, що в разі хибності вислову р вислів не-р є істинним.
Щоб дати означення логічного терміна заперечення, а також інших термінів, потрібно взяти за основу такі міркування. Кожне твердження, яке промовляє людина, вона подає адресатові мовлення як істинне. Наприклад, промовляючи кожне з наведених далі речень зі стверджувальною інтонацією (Людина є ссавцем; Завтра буде дощ; Сонце обертається навколо Землі), суб'єкт мовлення позначає цією інтонацією, що кожне з мовлених речень істинне. Очевидно, що насправді перше з цих речень істинне, значення істинності другого речення в момент мовлення невідоме і стане відомим лише наступного дня після мовлення, а третє речення є хибним. Тому, формулюючи означення змісту логічного терміна, достатньо назвати ті значення істинності простих тверджень-складників, які відповідають значенню "істинно" цього складного твердження.
Відповідно до зазначеного, заперечення - це логічний термін, яким мовець позначає, що твердження - складник складного твердження з цим терміном є фактично хибним. Наприклад, стверджуючи вислів Неправда, що особа А вчинила злочин, суб'єкт мовлення подає його як істинний. Так він подає вислів - складник цього складного вислову Особа А вчинила злочин як хибний.
Суть цього означення зафіксована в таблиці істинності. Коли мовець промовив твердження р, то подав його як істинне. Це позначено символом і (тобто істинно) в рядку з номером 2 під твердженням р. Цьому значенню істинності складного твердження р відповідає значення істинності х (тобто хибно) його твердження-складника р (що в таблиці позначено стрілкою):
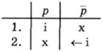
Зміст логічного терміна заперечення можна проілюструвати схемою, зображеною нижче (коли ціле складне твердження Неправда, що падає дощ подали як істинне, то словами неправда, що позначили, що твердження падає дощ, хибне).
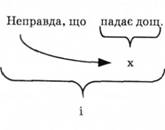
Слова "неправда, що..." вживають, зазвичай, для заперечення кимось попередньо сформульованого твердження. Частіше цей термін виражають заперечною часткою "не". Отже, речення Неправда, що падає дощ і Дощ не падає є синонімами, тобто виражають одне твердження.
Бінарних логічних термінів, тобто таких, якими позначено значення істинності двох тверджень, є 16. Проаналізуємо лише найпоширеніші з них.
Кон'юнкція - це логічний термін, яким мовець позначає, що обидва вислови-складники складного вислову фактично істинні. Наприклад, стверджуючи Свище вітер і падає дощ, мовець подає цей вислів як фактично істинний і так повідомляє адресата мовлення, що обидва прості вислови-складники {свище вітер і падає дощ) фактично істинні.
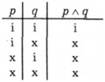
У сенсі кон'юнкції можна використовувати не тільки сполучник і. Наприклад, стверджуючи вислів Падає дощ, але світить сонце, мовець протиставним сполучником але повідомляє, що ці два явища (випадання дощу і світіння сонця), зазвичай, не бувають водночас, а от у момент мовлення вони одночасні. Проте мовець і перше речення (Падає дощ) і друге (Світить сонце) подає як фактично істинні. Подібне є і в такому прикладі: Ще вчора було холодно, а сьогодні тепло. Протиставним сполучником а мовець позначає, що такої різкої зміни погоди, як звичайно, не буває, однак, як і в попередньому прикладі, обидва речення він подає адресатові мовлення як фактично істинні. Отже, якщо між реченнями наявний один із наведених нижче сполучників (і, а, але, хоч, проте, зате, однак), то цей сполучник є кон'юнкцією.
Сам термін кон'юнкція запам'ятати неважко, оскільки в українській мові є багато слів з префіксом латинського походження кон-9 який позначає об'єднання чогось, наприклад: конференція, конгрес - об'єднання людей для обговорення певних питань; конфедерація - об'єднання держав чи організацій; конденсатор - пристрій для об'єднання електричних зарядів, рідин чи газів.

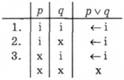
Диз'юнкція - це логічний термін, яким мовець позначає, що обидва твердження - складники складного твердження є фактично істинними або мають суперечливі значення фактичної істинності. Наприклад, ми зайшли до темної кімнати, в якій є лампочка розжарювання, натиснули на вмикач, але світла немає. Для пояснення цього факту ми формулюємо речення У мережі розрив, або нема напруги (коли лампочка перегоріла, то це один із варіантів розриву в мережі). Словом або, вжитим у сенсі диз'юнкції, мовець позначає, що в разі істинності складного твердження з цим терміном можливий один з трьох варіантів:
1) обидва прості твердження істинні;
2) перше з них істинне, а друге - ні;
3) перше з них хибне, але друге істинне.
У кожному з цих трьох випадків лампочка не буде світитися.
На відміну від кон'юнкції, якою мовець однозначно позначає значення істинності простих тверджень-складників, у разі диз'юнкції мовець повідомляє не один, а три варіанти значень істинності тверджень-складників. Істинності складного твердження (р V ц) в таблиці істинності відповідають три перші варіанти значень істинності тверджень р і q. Суб'єкт мовлення не знає, який із цих варіантів відповідає дійсності, або знає, але не хоче сказати.
Основою для створення символу диз'юнкції є перша літера латинського слова vel, яке означає або. Термін диз'юнкція також неважко запам'ятати, оскільки в українській мові є багато слів з префіксом диз- або його варіантами дис-, дез-, дес-, що означають роз'єднання чогось, наприклад, дисгармонія, диспропорція, дисонанс, деструкція, дезорганізація.
Слово або може бути вжитим також в іншому сенсі. Одним із можливих варіантів значення слова або є логічний термін сильна (строга) диз'юнкція (у цифровій електроніці

цей логічний термін трапляється під назвою виключне або чи роздільне або).
Сильна (строга) диз'юнкція - це логічний термін, яким мовець позначає, що твердження - складники складного твердження мають протилежні значення фактичної істинності (або перше істинне, а друге хибне, або перше хибне, а друге істинне). Наприклад: Переможцем у фінальній грі стане А, або кубок чемпіонату здобуде В. Промовивши це речення зі стверджувальною інтонацією, мовець подав відповідне твердження як істинне, а в разі істинності складного твердження (р^<?) твердження ріц можуть мати лише суперечливі значення істинності, що й відображено в таблиці істинності сильної диз'юнкції.
Щоб адресат мовлення однозначно зрозумів, що слово або вжите в сенсі сильної диз'юнкції, мовець може вжити такі формулювання: Або або... чи Одне з двох: ... або ... . У такому разі речення, запропоноване як приклад, можна сформулювати так: Або переможцем у фінальній грі стане А, або кубок чемпіонату здобуде В; в іншому варіанті - Одне з двох: переможцем у фінальній грі стане А, або кубок чемпіонату здобуде В. Хоч у цьому реченні слово або вжите один раз, зі слів одне з двох зрозуміло, що вислови - складники цього складного вислову не можуть бути ані обидва істинними, ані обидва хибними.
Слово або може бути вжите ще в третьому значенні. Логічний термін, який відповідає третьому значенню слова або, називають антикон'юнкцією. Анти-кон'юнкція - це логічний термін, яким мовець позначає, що вислови - складники складного вислову обидва є фактично хибними (див. найнижчий рядок таблиці істинності), або їхнє значення фактичної істинності суперечливе (другий і третій рядки таблиці істинності). Наприклад, комерсант закупив товар і формулює твердження

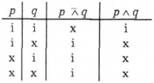
про можливі результати комерційної діяльності: прибуток або втрата. Може трапитися, що є прибуток і немає втрати (другий рядок таблиці істинності), нема прибутку і є втрата (третій рядок таблиці), нема ні прибутку, ні втрати (четвертий рядок таблиці). Останній із цих трьох варіантів відповідає випадкові, який позначають словами За що купив, за те продав, тобто витрати на придбання товару дорівнюють прибутку від його реалізації (ліпше продати без прибутку і купити новий товар, аніж намагатися отримати прибуток за умов, коли для цього немає об'єктивних підстав).
Антикон'юнкція є в працях з логіки також під назвою штрих Шеффера (за прізвищем американського вченого, який увів термін у логіку). Цей логічний термін у працях з логіки інколи позначають штрихом: (р | <?). Однак і назва терміна антикон'юнкція, і символьне його позначення кон'юнкцією, над якою розташований символ заперечення, є зручнішими, оскільки полегшують запам'ятовування. Справді, у тому рядку, де кон'юнктивне твердження має значення істинності "істинно", твердження з анти-кон'юнкцією має значення істинності "хибно", і навпаки, у тих рядках, у яких кон'юнктивне твердження має значення істинності "хибно", твердження з антикон'юнкцією має значення істинності "істинно".
Для аналізу логічних термінів диз'юнкція, строга диз'юнкція, антикон'юнкція, кожен з яких можна позначити словом або, вибрано такі приклади, щоб, аналізуючи зміст цих речень, можна було однозначно зрозуміти, в якому сенсі вжито сполучник або. Однак у процесі мовлення можуть траплятися випадки, коли зі змісту речення ми не можемо зрозуміти, в якому значенні вжито сполучник або. У такому разі треба перепитати співрозмовника, в якому сенсі віп використав цей сполучник. Наприклад, батьки, домовляючись про те, хто піде до школи забрати дитину, можуть сформулювати речення так: По дитину до школи підеш ти,
або я після уроків заберу її додому. В цьому реченні слово або можна розуміти і в сенсі диз'юнкції (може прийти або один із батьків, або інший, або обоє), і в сенсі сильної диз'юнкції (треба, щоб тільки хтось один із них пішов до школи по дитину, а інший, наприклад, повинен сидіти вдома, чекаючи важливого телефонного дзвінка). Власне тому, що слово або може бути вжитим в одному з трьох значень, воно є неоднозначним. Серед трьох аналізованих логічних термінів тільки сильну диз'юнкцію можна позначити або однозначно, або неоднозначно. Для слабкої диз'юнкції й антикон'юнкції однозначних слів чи словосполучень немає.
Інший логічний термін, яким позначають значення істинності тверджень, є імплікація. Імплікація - це логічний термін, яким мовець позначає, що твердження - складники складного твердження мають однакові значення фактичної істинності, або умова є хибною, а наслідок - істинним. Умову позначають символом, розміщеним ліворуч від знака імплікації, а наслідок, відповідно, - праворуч. У виразі (р -q) умовою є твердження, позначене символом р, а наслідком - твердження, позначене символом
Мовець, сказавши, наприклад, речення Якщо падає дощ, то на небі є хмари, нічого не повідомляє про те, чи є дощ і чи є хмари; він лише повідомляє, що можливий один з трьох варіантів:
1) є і дощ, і хмари (перший рядок таблиці істинності);
2) немає дощу, але є хмари (третій рядок таблиці істинності);
3) немає ні дощу, ні хмар (нижній, тобто четвертий рядок таблиці істинності).
У процесі з'ясування, який логічний термін є між реченнями, треба враховувати такі зауваги:
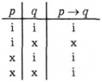
1. З'ясуємо, наприклад, який логічний термін є у твердженні Якщо число закінчується на нуль (крім нуля), то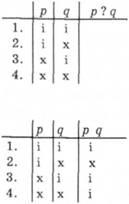 це число ділиться на п'ять без остачі. Для цього треба дати відповідь на питання: чи існує такий стан, який зафіксовано кожним із чотирьох рядків таблиці, зображеної праворуч? Якщо рядком зафіксовано реальний стан справ, тобто те, що буває, є насправді, то в останньому стовпці рядка ставимо символ і, якщо ні, - то символ х. Першим рядком таблиці зафіксовано, що обидва твердження істинні; оскільки таке буває, що число закінчується на нуль і ділиться на п'ять без остачі, то в останньому стовпці цього рядка ставимо символ і. Другий рядок таблиці відображає, що перше твердження є істинним, а друге - ні, тобто що число закінчується на нуль, а на п'ять без остачі не ділиться; оскільки такого не буває, то в третьому стовпці цього рядка ставимо символ х. Третім рядком зафіксовано, що число не закінчується на нуль, але ділиться на п'ять без остачі; таке буває у разі, коли число закінчується на п'ять, тож в останньому стовпці третього рядка ставимо символ і. У четвертому рядку зафіксовано, що обидва твердження є хибними, тобто число не закінчується на нуль і не ділиться на п'ять без остачі. Таке трапляється, тож в останньому стовпці четвертого рядка ставимо символ і.
це число ділиться на п'ять без остачі. Для цього треба дати відповідь на питання: чи існує такий стан, який зафіксовано кожним із чотирьох рядків таблиці, зображеної праворуч? Якщо рядком зафіксовано реальний стан справ, тобто те, що буває, є насправді, то в останньому стовпці рядка ставимо символ і, якщо ні, - то символ х. Першим рядком таблиці зафіксовано, що обидва твердження істинні; оскільки таке буває, що число закінчується на нуль і ділиться на п'ять без остачі, то в останньому стовпці цього рядка ставимо символ і. Другий рядок таблиці відображає, що перше твердження є істинним, а друге - ні, тобто що число закінчується на нуль, а на п'ять без остачі не ділиться; оскільки такого не буває, то в третьому стовпці цього рядка ставимо символ х. Третім рядком зафіксовано, що число не закінчується на нуль, але ділиться на п'ять без остачі; таке буває у разі, коли число закінчується на п'ять, тож в останньому стовпці третього рядка ставимо символ і. У четвертому рядку зафіксовано, що обидва твердження є хибними, тобто число не закінчується на нуль і не ділиться на п'ять без остачі. Таке трапляється, тож в останньому стовпці четвертого рядка ставимо символ і.
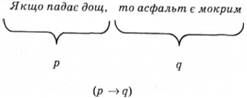
2. У процесі з'ясування того, який логічний термін є в реченні, треба враховувати, що, формулюючи певну думку, певне знання, суб'єкт мовлення може опускати частину слів, тобто частину цих знань, передбачаючи, що адресат мовлення зрозуміє неозвучене з контексту (для економії мислення, мовлення). Проаналізуємо такий приклад: Якщо падає дощ, то асфальт є мокрим. Для з'ясування того, який логічний термін є у цьому твердженні, треба відповісти на питання: чи існує такий стан, який зафіксовано кожним з чотирьох рядків таблиці, наведеної праворуч? Якщо якимось із рядків позначено таке, що існує, то в останньому стовпці у цьому рядку ставимо символ і, якщо ні, - то
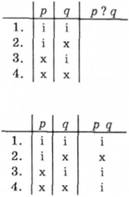
символ х. Першим рядком таблиці зафіксовано, що обидва твердження є істинними; оскільки буває, що падає дощ і асфальт мокрий, то в останньому стовпці цього рядка ставимо символ і. Другим рядком таблиці позначено, що перший вислів є істинним, а Другий - ні, тобто що дощ падає, а асфальт не є мокрим; оскільки такого не буває, то в третьому стовпці цього рядка ставимо символ х. Третім рядком зафіксовано, що дощу немає, а асфальт мокрий - таке буває, оскільки асфальт може бути мокрим з інших причин, тож в останньому стовпці третього рядка ставимо символ і. У четвертому рядку зафіксовано, що обидва вислови є хибними, тобто немає дощу і асфальт не є мокрим. Таке буває, тож в останньому стовпці у четвертому рядку ставимо символ і.
Однак у декого може виникнути питання: а якщо над асфальтом є якийсь дашок, парасоля, розлоге дерево, авто тощо? У такому разі можливо, що перший вислів істинний (дощ падає), а другий - хибний (тобто насправді асфальт не є мокрим). У такому випадку в останньому стовпці другого рядка треба ставити символ і. Отже, цей логічний термін не є імплікацією? У наведеному прикладі треба враховувати таке. У процесі мовлення людина намагається висловити думку за допомогою мінімальної кількості слів, тому, коли ми передбачаємо, що адресат мовлення зрозуміє: йдеться про той випадок, коли над асфальтом немає поверхні, непроникної для дощу, то ми цього не вимовляємо. Коли ж припускаємо, що суб'єкт мовлення може не зрозуміти цього, то думку треба формулювати повністю: Якщо падає дощ, то асфальт, над яким немає поверхні, непроникної для дощу, є мокрим. У разі повного викладу думки в адресата мовлення вже не можуть виникнути сумніви щодо другого рядка таблиці - такого, щоб падав дощ, а асфальт, над яким немає поверхні, непроникної для дощу, був сухим, не може бути, тож у третьому стовпці в другому рядку треба ставити символ х. (Якщо мовець хоче сказати про той випадок, що над асфальтом може не бути, але може й бути поверхня, непроникна для дощу, то в другому рядку третього стовпця треба також поставити значення "істинно"; оскільки в усіх чотирьох випадках поєднань ознак, відповідних аргументам, складне твердження набуває значення "істинно", то це означає, що безпосереднього зв'язку зумовлення між цими ознаками нема, а в такому разі зв'язок між ними треба формулювати не словами "Якщо..., то...", а словами - "Безпосереднього зв'язку нема").
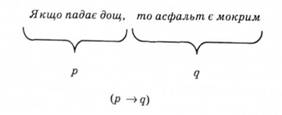
3. Логічним терміном "імплікація", позначають відношення умова - наслідок. Це не обов'язково відношення причинно-наслідкове, як у прикладі Якщо падає дощ, то асфальт є мокрим. Зокрема, у реченні Якщо падає дощ, то на небі є хмари логічний термін - також імплікація, однак очевидно, що наявність дощу не є причиною хмар, а навпаки.
4. У реченнях природної мови умова може бути розміщена як перед наслідком, так і після нього. Натомість у символьному виразі (р->#) прийнято першим символом, тобто символом р, позначати умову, а другим символом, тобто символом </, - наслідок, незалежно від того, як вони розміщені одне щодо одного в реченні. Наприклад, у реченні Якщо падає дощ, то асфальт є мокрим умова (речення, яке починається зі слова якщо) розміщена перед наслідком, а в реченні Асфальт є мокрим, якщо падає дощ умова розташована після наслідку. Позначивши умову символом р, а наслідок символом q, і перше речення, і друге запишемо однаковим виразом (р -> д).
5. Логічний термін імплікація можна сформулювати словесно різним способом. Наявні два варіанти однозначного формулювання імплікативного зв'язку між твердженнями. Ці варіанти актуальні у разі, якщо нам важливо, щоб адресат мовлення однозначно зрозумів, що логічний термін є імплікацією, і, наприклад, не міг посилатися на те, що, мовляв, це формулювання можна було тлумачити по-різному, і він, отже, не так зрозумів. Однозначні формулювання імплікації такі:
1)тоді, але не тільки тоді ... . Наприклад, Тоді, але не тільки тоді, коли падає дощ, асфальт є мокрим;
2)... є достатньою, але необов'язковою (не необхідною) умовою ... . Наприклад, Падіння дощу є достатньою, але не обов'язковою умовою мокроти асфальту.
Є також два варіанти неоднозначного формулювання імплікативного зв'язку між твердженнями (актуальні у випадку, якщо суб'єкт мовлення бажає висловитися неоднозначно, щоб у разі, коли адресат зрозумів мовлене в одному значенні, можна було сказати, що йшлося про інше). Неоднозначні формулювання імплікативного зв'язку між твердженнями такі:
1) якщо то ... . Наприклад, Якщо йде дощ, то асфальт с мокрим;
2) потрібно щоб ... . Наприклад, Потрібне випадання дощу, щоб асфальт був мокрим.
Неоднозначними ці формулювання є через те, що ними можна виразити ще два логічні терміни, отже, адресат
мовлення може не зрозуміти, в якому сенсі вжиті слова, які є логічним терміном.
Інший логічний термін, який позначає відношення умова - наслідок, називають реплікацією. Реплікація - це логічний термін, яким мовець позначає, що обидва твердження - складники складного твердження мають однакові значення фактичної істинності, або умова є істинною, а наслідок - хибним. Наприклад, Якщо доведено факт існування угоди, то угода має юридичні наслідки. (Якщо угода має юридичні наслідки, то це означає, що в разі невиконання якоюсь зі сторін узятих на себе зобов'язань її примушують виконати ці зобов'язання через суд). Промовивши це речення зі стверджувальною інтонацією, тобто подавши це складне твердження як фактично істинне, суб'єкт мовлення повідомляє адресата мовлення, що можливим є один із трьох варіантів:
1) обидва прості твердження-складники є істинними (перший рядок зі значеннями істинності в таблиці), тобто істинно і те, що доведено факт існування угоди, і те, що вона має юридичні наслідки;
2) умова, тобто твердження, позначене символом р (факт існування угоди доведено), - істинна, а наслідок, тобто твердження, позначене символом q (угода має юридичні наслідки), є хибне (третій рядок зі значеннями істинно); це можливе за умови, коли не дотримано всіх вимог до угод, наприклад, можна довести, що укладено угоду, однак вона була усною, або не стосувалася таких питань, за які законодавством передбачено юридичну відповідальність, тож доведення факту існування угоди було недостатньо для того, щоб вона мала юридичні наслідки;
3) обидва прості твердження-складники є хибними (нижній, тобто четвертий рядок зі значеннями істинності в таблиці), тобто хибно і те, що доведено факт існування угоди, і те, що вона має юридичні наслідки.
Однозначні формулювання реплікативного зв'язку між твердженнями такі:
1) тільки тоді ... . Наприклад, Тільки тоді, коли доведено факт існування угоди, вона має юридичні наслідки;
2)... є обов'язковою (необхідною), але недостатньою умовою ... . Наприклад, Доведення факту існування угоди є обов'язковою, але не достатньою умовою того, що вона має юридичні наслідки.
Неоднозначні формулювання реплікативного зв'язку між твердженнями такі;
1)якщо то ... . Наприклад, Якщо доведено факт існування угоди, то вона має юридичні наслідки;
2) потрібно щоб ... . Наприклад, Потрібно довести факт існування угоди, щоб вона мала юридичні наслідки.
Ще один логічний термін, яким позначають відношення умова - наслідок, називають еквіваленцією. Еквіваленція - це логічний термін, яким мовець позначає, що обидва твердження-складники складного твердження мають однакові значення фактичної істинності. Наприклад: Якщо сьогодні понеділок, то завтра вівторок. Це твердження є істинним у першому (тобто мовець позначає, що обидва прості твердження-складники є істинними - істинне і те, що сьогодні понеділок, і те, що завтра вівторок) і четвертому рядках таблиці істинності (тобто мовець позначає, що обидва прості твердження-складники є хибними - хибне і те, що сьогодні понеділок, і те, що завтра вівторок). Не може бути тільки такого, щоб сьогодні був понеділок, а завтра не був вівторок (другий рядок таблиці), і таке, щоб сьогодні не був понеділок, а завтра був вівторок (третій рядок таблиці); тому у третьому стовпці в цих рядках поставлено символ х, тобто хибно.
Однозначні формулювання еквіваленції у природному мовленні такі:

1) тоді, і тільки тоді... . Наприклад, Тоді, і тільки тоді, коли сьогодні є понеділок, завтра буде вівторок;
2)... є обов'язковою (необхідною) і достатньою умовою ... . Наприклад, Те, що сьогодні є понеділок, є обов'язковою й достатньою умовою того, що завтра буде вівторок.
Неоднозначні формулювання еквіваленції у природному мовленні такі:
1)якщо то ... . Наприклад, Якщо сьогодні понеділок, то завтра вівторок;
2) потрібно щоб ... . Наприклад, Потрібно, щоб сьогодні був понеділок, для того, щоб завтра був вівторок.
Для ідентифікації логічних термінів потрібно керуватися такими міркуваннями:
1)якщо речення починається зі слів "Неправда, що...", то це є логічний термін "заперечення";
2) якщо між реченнями наявний один із наведених нижче сполучників (і, а, але, хоч, проте, зате, однак), то цей сполучник є кон'юнкцією. (Сполучник і можна вживати також для позначення причинно-наслідкових зв'язків, як це є, наприклад, у реченні "Випав сніг, і все навколо стало білим");
3) якщо вжито сполучник або, то це один із трьох наведених нижче логічних термінів (диз'юнкція, строга диз'юнкція, антикон'юнкція). Якщо вжито сполучник або..., або...; то..., то...; чи то..., чи то...; не то..., не то..., або речення починається словами Одне з двох:...", то це сильна диз'юнкція;
4) якщо вжито сполучники якщо..., то... або потрібно..., щоб..., то це один із трьох наведених нижче логічних термінів (імплікація, реплікація, еквіваленція):
- якщо вжито одне з наведених нижче формулювань ("Тоді, але не тільки тоді, коли..." або "...достатня, але не обов'язкова (необхідна) умова..."), то це імплікація;
- якщо вжито одне з наведених нижче формулювань ("Тільки тоді, коли..." або "...обов'язкова (необхідна), але недостатня умова..."), то це реплікація;
- якщо вжито одне з наведених нижче формулювань ("Тоді і тільки тоді..." або "Достатня й обов'язкова (необхідна) умова..."), то це еквіваленція;
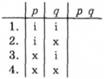
5) якщо важко визначити, який логічний термін вжито, то потрібно побудувати порожню таблицю (табл. 1.1) і для кожного з чотирьох варіантів комбінацій значень істинності рід з'ясувати, чи може це складне твердження бути істинним. Наприклад, проаналізуємо твердження "Якщо кожен із доданків є парним числом, то сума є парним числом".
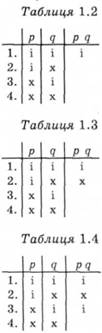
Для кожної з чотирьох комбінацій значень істинності даємо відповідь на запитання: чи можуть твердження-складники мати відповідні значення істинності? Якщо так, то в останньому стовпці у відповідному рядку ставимо і (істинно), якщо ні, то - х ("хибно"). Згідно з першою комбінацією значень істинності, обидва твердження є істинні. Оскільки трапляються випадки, коли обидва твердження-складники, що містяться в наведеному вище прикладі, істинні, то в останньому стовпці першого рядка ставимо і (табл. 1.2). Такого, щоб перше твердження ("кожен із доданків є парним числом") було істинним, а друге ("сума є парним числом") - хибним, бути не може, тому в другому рядку останнього стовпця ставимо х (табл. 1.3). Випадок, коли перше твердження-складник ("кожен із доданків є парним числом") є хибне, а друге ("сума є парним числом") - істинне, можливий (коли обидва доданки непарні). Тому в третьому рядку останнього стовпця ставимо і (табл. 1.4). Можливий також випадок, коли обидва твердження-складники є хибні (неправда і те, що обидва доданки непарні, і те, що сума непарна). Тому в четвертому рядку останнього стовпця ставимо і (табл. 1.5). У підсумку ми отримали таблицю істинності імплікації, отже, вираз "якщо..., то..." в аналізованому прикладі є імплікацією, що й фіксуємо відповідним символом (табл. 1.6).
Таблиця 1.1

ОЗНАЧЕННЯ
Альтернатива - умови, за яких треба вибирати один з двох варіантів (формально альтернативу записують сильною диз'юнкцією).
Аптикон'юнкцією (це одне зі значень сполучника або) позначають, що принаймні одне з двох тверджень хибне (принаймні одне явище відсутнє).
Диз'юнкцією (це одне зі значень сполучника або) позначають, що принаймні одне з двох тверджень істинне (принаймні одного явища нема).
Еквіваленцією позначають, що твердження мають однакові значення істинності (обидва явища або водночас наявні, або водночас їх нема).
Запереченням (словами неправда, що) позначають, що твердження, розміщене після цих слів, є хибним (відповідного явища нема).
Імплікацією позначають, що твердження мають однакові значення істинності або те, що умова хибна, а наслідок істинний.
Кон'юнкцією (сполучниками і, й, та, а, але, проте, зате, хоча, однак) позначають, що обидва твердження, з'єднані таким сполучником, істинні (обидва явища наявні).
Просте твердження - твердження, що не містить слів, якими позначають значення істинності тверджень, тобто твердження, в якому міститься тільки логічний термін "істинно".
Реплікацією позначають, що твердження мають однакові значення істинності або те, що умова є істинна, а наслідок хибний.
Сильною диз'юнкцією (це одне зі значень сполучника або) позначають, що тільки одне з двох тверджень істинне (тільки одне явище наявне).
Складне твердження - твердження, що містить будь-який інший логічний термін, крім терміна "істинно" (відповідне речення містить слова, якими позначають значення істинності тверджень (наприклад, і; але; або; неправда, що та ін., крім слова істинно).
Твердження - зміст розповідного речення.
1.2. Зміст логічних термінів
ЛЕКЦІЯ 2. Виявлення несумісності знань
2.1. Види несумісності знань
2.2. Суперечність між твердженнями тексту
Інструменти. Алгоритм виявлення суперечності у послідовності пов'язаних тверджень
2.3. Суперечливі складні твердження
Інструменти. Алгоритм виявлення суперечності у послідовності пов'язаних тверджень
2.4. Закони логіки
ЛЕКЦІЯ 3. Виведення знань