Логіка - Дуцяк І.3. - 4.2. Відношення між іменами за обсягом (логічні терміни у простому твердженні)

Залежно від того, чи мають обсяги імен спільні елементи, між іменами виникають різні відношення (цим відношенням відповідає математичний апарат відношення множин) (рис. 4.3).

Якщо імена не мають спільних елементів, то таке відношення називають несумісністю. Графічно це відношення зображають двома колами, які не мають спільних точок, тобто жодна точка одного кола не міститься в іншому. В такому відношенні перебувають імена планета (5) і зоря (Р) - жодна планета не є зорею; відношення несумісності є також між іменами криволінійна замкнута фігура (£) і багатокутник (Р) - жодна криволінійна замкнута фігура не є багатокутником.

Відношення між іменами, за якого їхні обсяги мають спільні елементи, називають сумісністю. Можливі три варіанти сумісності: рівнообсяговість, підпорядкованість, перехрещеність. Рівнообсяговість - це таке відношення між іменами, за якого кожен елемент обсягу першого імені є елементом

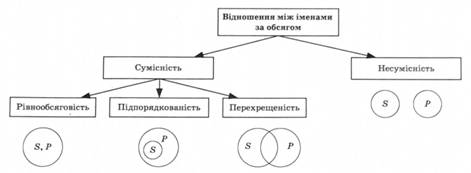
Рис. 4.3. Відношення між іменами за обсягом

обсягу другого, і навпаки. Графічно це виявляється в тому, що кожна точка з одного кола є одночасно точкою іншого кола, і навпаки. Наприклад: 5 - планета, розташована третьою від Сонця, Р - планета, заселена людьми. Це назви одного й того самого об'єкта за різними ознаками (в одному випадку - за порядком розташування, а в іншому - за наявністю на цій планеті людей). Інший приклад: 5 - рівносторонній трикутник і Р - рівнокутний трикутник (кожен рівносторонній трикутник є рівнокутним і кожен рівнокутний є рівностороннім). Підпорядкованість - це таке відношення між іменами, за якого кожен елемент обсягу одного імені є елементом обсягу другого, але не навпаки, тобто не кожен елемент обсягу другого імені є елементом обсягу першого. Графічно це виявляється в тому, що кожна точка, яка міститься в меншому колі, міститься також і в більшому колі, але не навпаки. Наприклад, 5 - орел і Р - птах. Кожен орел є птахом, але не кожен птах є орлом. Більш загальне ім'я називають родовим, а менш загальне - видовим (крім випадку, коли підпорядковані імена є одиничними). Перехрещеність - це таке відношення між іменами, за якого наявні три множини об'єктів:

1) об'єкти, які є елементами обсягу першого імені, але не є елементами обсягу другого;

2) об'єкти, які є елементами обсягу другого імені, але не є елементами обсягу першого;

3) об'єкти, які є елементами обсягів обох імен.

Наприклад, 5 - хижак і Р - ссавець. Існують хижаки, які не є ссавцями, ссавці, які не є хижаками, та істоти, які є і хижаками, і ссавцями.

у зазначені вище відношення можуть вступати тільки ті імена, які мають спільне більш загальне ім'я - такі імена називають порівнюваними. Наприклад, імена стіл і справедливість не є несумісні: оскільки вони не мають спільного більш загального імені, то їх треба зачислити до непорівнюваних. Водночас щодо імен стіл і крісло можна ставити питання Яке між ними відношення обсягів? Ці імена належать до порівнюваних, оскільки мають спільне більш загальне ім'я - меблі.

Інструменти. Алгоритм визначення відношення між обсягами імен 4 (відношення між множинами)

Для визначення відношення між обсягами імен 5 і Р потрібно послідовно дати відповіді на такі питання:

1. Чи існують об'єкти, які мають і ознаку в, і ознаку Р1

o Якщо - ні, то між іменами 5 і Р відношення несумісності.

o Якщо - так, то між цими іменами одне з трьох відношень сумісності.

2. Чи існують об'єкти, які мають ознаку Б і не мають ознаки Р, і навпаки, об'єкти, які мають ознаку Р, але не мають ознаки 5?

o Якщо ні перші, ні другі не існують, то між іменами 5 і Р відношення рівнообсяговості.

o Якщо і перші, і другі існують, то між іменами 5 і Р відношення перехрещеності.

o Якщо перші (об'єкти, які мають ознаку 5 і не мають ознаки Р) існують, а другі (об'єкти, які мають ознаку Р, але не мають ознаки 5) не існують, то Р підпорядковане 5, а якщо навпаки, другі існують, а перші - ні, то 5 підпорядковане Р.

Приклад 1: визначення відношення між обсягами імен економіст і вчений.

Даючи відповідь на перше питання, отримуємо: люди, які є водночас і економістами, і вченими, - існують, отже, між цими іменами є одне з трьох відношень сумісності.

Відповідаючи на друге питання, отримуємо: оскільки існують і економісти, які не є вченими, і вчені, які не є економістами, то між цими іменами є відношення перехрещеності.

Приклад 2: визначення відношення між обсягами імен людина, юрист.

Даючи відповідь па перше питання, отримуємо: істоти, які є водночас і людьми, і юристами, - існують, отже, між цими іменами є одне з трьох відношень сумісності. Відповідаючи на друге питання, отримуємо: оскільки люди, які не є юристами існують, а юристи, які не є людьми, - - не існують, то ім'я юристи є підпорядковане імені люди, юристи є видом людей.

Потрібно відрізняти відношення підпорядкованості від інших видів відношень. Зокрема, треба відрізняти родовидові відношення від відношень частина - ціле та від відношень ознака - прояв ознаки. Наприклад, між іменами форма і кулястість нема відношення імен за обсягом - між ними відношення ознака - прояв ознаки. Не можна сказати, що кулястість є видом форми. Типи ознак (такі як форма) не поділяють на види, вони мають різні ступені та видозміни прояву.

Щоб відрізнити відношення підпорядкованості від відношення частина - ціле, треба керуватися таким міркуванням. Якщо певним іменем позначено частину об'єктів, позначуваних іншим іменем, то між відповідними іменами є відношення підпорядкованості. Якщо певним іменем позначено частину об'єкта, позначуваного іншим іменем, то це є відношення частина - ціле. Наприклад: мопеди є частиною колісних транспортних засобів, отже, між іменами колісний транспортний засіб і мопед є відношення підпорядкованості. Однак колесо є частиною колісного транспортного засобу, тому між іменами колісний транспортний засіб і колесо є відношення частина - ціле.

Крім того, щоб переконатися, чи між аналізованими іменами Й і Р є відношення підпорядкованості, треба сформулювати твердження "Р є видом 5". Якщо це формулювання відповідатиме дійсності, то між аналізованими іменами справді є відношення підпорядкованості. Наприклад, чи є між іменами транспортний засіб і мопед відношення підпорядкованості? Твердження Мопед є видом транспортних засобів відповідає дійсності, отже, між аналізованими іменами є відношення підпорядкованості. Натомість твердження Колесо є видом мопеда не відповідає дійсності, отже, між цими іменами нема відношення підпорядкованості.

Інколи у процесі з'ясування виду відношень між обсягами виникає думка, що відношення обсягів імен можна зобразити двома колами, які мають одну точку дотику. У цьому разі вважають, що обсяги імен мають один спільний елемент. Водночас наявність спільних елементів (неважливо скільки їх - один чи більше одного) є відношенням перехрещеності, яке графічно позначають відповідною діаграмою двох полів, частково накладених одне на одне. Тому зображення двох кіл з однією точкою дотику - це дублювання графічного зображення відношення перехрещеності, що є некоректним.

Для з'ясування змісту тверджень, що формулювання правил виведення знань потрібно володіти системою всіх можливих відношень між іменами за обсягом. Види відношень візуалізують за допомогою діаграм Ейлера. У деяких навчальних виданнях наводять, окрім інших, такі відношення між іменами за обсягом, як співпідпорядкованість, протилежність, суперечність. Однак такий підхід є некоректним. Адже коли зображають, наприклад, відношення підпорядкованості, то на діаграмі відтворюють лише два кола (рис. 4.4, а), тоді як на зображенні співпідпорядкованості чи протилежності (рис. 4.4, б, в) - три поля, тобто це фактично вже відношення не між двома іменами, а між трьома. Три множини об'єктів зображено також на діаграмі суперечності (рис. 4.4, г); з'єднавши два поля так, що вони в сукупності позначають обсяг загальнішого поняття, ми насправді зобразили і це загальніше поняття, демонструючи, що, крім цих двох множин об'єктів, загальніше поняття не містить інших об'єктів.

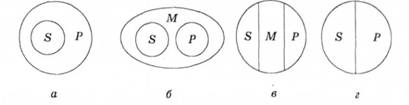
Рис. 4.4. Відношення: а - підпорядкованості; б - співпідпорядкованості; в - протилежності; г - суперечності

Коректнішим є уявлення, що між обсягами імен може бути тільки п'ять видів відношень (це так звані жергонові відношення між обсягами імен). Справді, є лише п'ять способів розміщення одного кола щодо іншого (рис. 4.5). Водночас якісно різних відношень є чотири, оскільки відношення підпорядкованості має два варіанти - коли перше ім'я підпорядковане другому, і навпаки. Однак цих п'яти видів відношень недостатньо для аналізу навіть безпосередніх виводів. Це пов'язане з тим, що нехтування обсягом загальнішого імені, теми мовлення, тобто універсуму, може призводити до обмеженості правил виведення, сформульованих на підставі виділених лише цих чотирьох видів відношень. Проаналізуємо такі приклади.

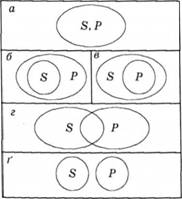
Рис. 4.5. Жергонові відношення: а - рівнообсяговість; б і в - підпорядкованість; г - перехрещеність; ґ - несумісність

Приклад 1. Темою мовлення є плоскі багатокутники. Із твердження Жоден трикутник не є чотирикутником операцією протиставлення предикатові виведемо: Частина плоских багатокутників, які не є чотирикутниками, є трикутниками (рис. 4.6, а).

Приклад 2. Темою мовлення є цілі числа. Із твердження Жодне парне число не е непарним операцією протиставлення предикатові виведемо Усі числа, які не є непарними, є парними (рис. 4.6, б).

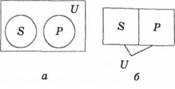
Рис. 4.6. Види несумісності: а - S - трикутники, Р - чотирикутники, U - плоскі багатокутники; б - S - парт числа, Р - непарні числа, U - цілі числа

Отже зі загальнозаперечного твердження внаслідок протиставлення предикатові в одному випадку несумісності потрібно виводити частковостверджувальне твердження, а в іншому - загальностверджувальне. Оскільки для виведення нам не байдуже, чи містить універсум ще якісь об'єкти, крім Б і Р, чи ні, то п'ять жергонових діаграм треба подвоїти - у половині з них універсум не містить об'єктів, які не мають ні ознаки б, ні ознаки Р, а в половині - містить. У підсумку отримано десять діаграм (і, відповідно, десять різних тверджень).

Щоб отримати переконаність, що виявлено всі види відношень за обсягом, можна застосувати інші способи візуалізації цих відношень, деякі з яких наведені нижче (рис. 4.7). Найбільш наочними серед них є діаграми Ейлера і Венна.

Головна відмінність між діаграмами Ейлера й Венна полягає в тому, що на діаграмах Ейлера окремими полями позначено тільки об'єкти, які існують, тобто не порожні

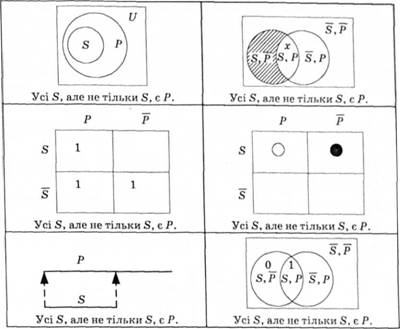
Рис. 4.7. Візуалізація відношення за обсягом: а - діаграми Ейлера; б - діаграми Венна; в - діаграми Карго-Вейга; г - діаграми Льюїса Корола; ґ - лінійні діаграми; д - комбіновані діаграми

множини, тоді як на діаграмах Венна окремими полями позначено всі можливі об'єкти, тобто об'єкти з усіма можливими варіантами поєднання двох чи більше ознак. На діаграмі Венна є три види графічних знаків:

1) полем, на якому поставлений хрестик, позначають об'єкти, які існують;

2) заштрихованим полем позначають об'єкти, які не існують;

3) не заштрихованим полем без хрестика позначають, що в одних випадках об'єкти, позначені цим полем, можуть існувати, а в інших - ні, тобто невідомо, чи ці об'єкти існують.

Для виявлення всіх можливих відношень між іменами за обсягом важливо те, що можна визначити однозначну відповідність між діаграмами Венна та булевими функціями, тобто тими логічними термінами, про які йшлося у темі Логічний аналіз складних тверджень (кон'юнкція, диз'юнкція та ін.). Для з'ясування відповідності між відношеннями за обсягом та логічними функціями (йдеться про булеві функції) використаємо діаграми Венна, на яких є два види позначень:

1) незаштрихованим полем без хрестика позначають об'єкти, які існують;

2) заштрихованим полем позначають об'єкти, які не існують.

Розглянемо твердження Усі 8, але не тільки 5, є Р, графічне зображення якого відтворене на рис. 4.8:

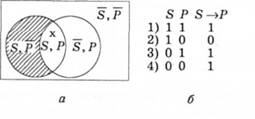
Рис. 4.8. Діаграма Венна, якою зафіксоване: а - відношення обсягів імен, відповідне вислову Усі в, але не тільки £, є Р; б - таблиця відповідної булевої функції

Оскільки об'єкти, які мають і ознаку 8, і ознаку Р, існують (відповідне поле на діаграмі Венна незаштриховане), то в першому рядку останнього стовпця таблиці ставимо 1. Оскільки об'єкти, які мають ознаку 5, але не мають ознаки Р, не існують (відповідне поле на діаграмі Венна заштриховане), то в другому рядку останнього стовпця таблиці ставимо 0. Оскільки об'єкти, які не мають ознаки 5, але мають ознаку Р, існують (відповідне поле на діаграмі Венна незаштриховане), то в третьому рядку останнього стовпця таблиці ставимо 1. Оскільки об'єкти, які не мають ні ознаки 5, ні ознаки Р, існують (відповідне поле на діаграмі

Венна незаштриховане), то в четвертому рядку останнього стовпця таблиці ставимо 1. У підсумку отримано таблицю імплікації, тобто відношення підпорядкованості обсягів імен можна зафіксувати у символьному вигляді виразом 5 -> Р.

Оскільки кількість логічних функцій є скінченна (їх шістнадцять), то такою є і кількість відношень між іменами за обсягом.

У природній мові, якою фіксують знання в разі мислення чи спілкування, є спеціальні слова для позначення відношення обсягів імен, тобто для позначення відношень між множинами. Ці логічні терміни виражають, зокрема, такими словами: "Усі ... є ..."; "Частина ... є ,.."; "Жоден ... не є "Частина ... не є ..."; "Певна кількість ... є ..."; "Певна кількість ... не є ..." та низка інших, які детально описані в лекції 5.