Зупинимося на другому елементові логічної структури поняття, на обсязі поняття.
Об с я г о м поняття називається множина предметів, кожен з яких є носієм ознак, що складають зміст поняття.
Наприклад, до обсягу поняття "столиця" входять предмети: "Київ", "Варшава", "Париж" і т. д. Але до обсягу цього поняття не ввійдуть предмети: "Харків", "Краків", "Нью-Йорк" тощо, тому що жоден з цих предметів не є носієм ознаки "бути столичним містом".
Можна ще й так сказати: обсягом поняття слід вважати коло предметів, на які поширюється це поняття. Наприклад, обсяг поняття "шахрайство" складають всі конкретні випадки злочинів, які мають ознаки, що складають зміст цього поняття; об'єм поняття "держава" - всі держави; об'єм поняття "конституція" - всі конституції конкретних держав і т.д.
Всі предмети, які входять до обсягу поняття, утворюють логічний клас. Логічний клас складається із індивідів. Індивідом логічного класу називається носій власного імені. Наприклад, "Франція" є індивідом класу держав з республіканською формою правління; "викрадення картини Караваджіо "Поцілунок Іуди"" є індивідом класу крадіжок; "замах на Павла II" є індивідом обсягу поняття "замах на умисне вбивство" і т.д.
Для того щоб встановити належність певного предмету до об'єму поняття, слід простежити, чи є він носієм всіх ознак, що складають зміст поняття без жодного виключення.
Ця обставина має важливе значення в слідчій практиці при встановленні юридичної оцінки різноманітних правових явищ, особливо при кваліфікації злочинів. Наприклад, якщо конкретне протиправне діяння не має хоча б однієї ознаки, що входить до складу такого злочину, як "шахрайство", то воно не може бути кваліфіковане як шахрайство і, таким чином, включеним в об'єм цього поняття.
Як ви звернули увагу, у самому визначенні обсягу поняття фігурує термін "множина". Справа у тому, що обсягом будь-якого поняття є деяка множина, а тому це дає можливість вивчити природу обсягу поняття, змоделювати його структурні, функціональні особливості на такому об'єкті як множина. Тобто, надалі для нас обсягом поняття буде множина і ми будемо з нею поводитися як обсягом конкретних понять. Така точка зору зумовлює необхідність визначити такий об'єкт як множина і охарактеризувати основні її ознаки.
М н о ж и н о ю називається будь-яка сукупність визначених і розрізнюваних між собою об'єктів мислимих як єдине ціле. Множина - це абстракція, в якій кожний предмет, що входить до неї розглядається лише з точки зору тієї ознаки, яка дозволила включити його до свого складу. Тому предмети, що складають множину не розрізнювані між собою (їм приписуються одні й ті самі ознаки).
Наприклад, множина книг, множина держав, множина рослин тощо. Для кожного із предметів, що входять у перераховані множини характерним є те, що для них усіх притаманні ознаки на основі яких утворені ці множини: "бути книгою", "бути державою", "бути рослиною".
Можна сказати, що предмети, які входять до множини розрізняються між собою. Але це розрізнення один від одного відбувається не за властивостями і відношеннями, а за їх іменами. Так у множині держав кожний із предметів як носій ознаки "бути державою" не відрізняється від іншого, але відрізняється як індивідуальність, як носій власного імені ("Україна", "Франція", "Аргентина" тощо).
Предмети, що належать до певної множини називаються елементами. Позначають їх малими буквами латинського алфавіту -
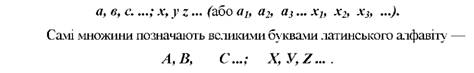
Множина, яка містить кінцеве число елементів називається скінченною (наприклад, множина планет Сонячної системи; множина формально-логічних законів тощо). А множина, яка має нескінченне число елементів називається нескінченою (наприклад, множина чисел, множина зірок, тощо).
Оскільки множини можуть складатися з об'єктів різноманітної природи це визначає їх універсальний характер і, як наслідок, дає можливість застосовувати їх в різноманітних галузях (математиці, біології, лінгвістиці тощо), а не тільки в логіці.
Між множиною та її елементом існує відношення належності. Належати до множини це означає бути носієм ознаки, на підставі якої ця множина утворена. Відношення належності позначається
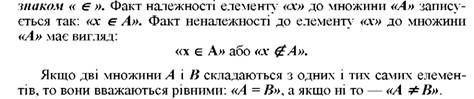
Існує два найуживаніших способи задання множин. Перший полягає у простому перерахуванні елементів, що складають дану множину. Наприклад, множина арифметичних дій, множина планет Сонячної системи тощо. Відповідно записується: А = {х1, х2, х3, х.4}, В = {х1, х2, х3,... х9}.
Отже, цей спосіб ефективний, коли мають справу із скінченними множинами. Коли ж розглядаються нескінченні множини, той цей спосіб не підходить. У цих випадках користуються іншим способом, який полягає у заданні множини через характеристичну властивість. Характеристичною називається властивість, яка належить будь-якому елементу даної множини, і не належить жодному предмету, що не входить до неї. Записується це так:
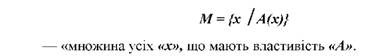
Спеціально необхідно виділити універсальну множину, тобто множину, яка складається із усіх елементів досліджуваної предметної області. Позначається універсальна множина буквою "II", а графічно зображується множиною точок у середині прямокутника:

Окрім універсальної множини виділяють порожню множину, тобто множину, яка не містить жодного елемента (наприклад, "дерево, яке проводить електричний струм", "метал, який легший повітря" тощо) . Позначається порожня множина символом: θ .
Будь-яку частину множини називають підмножиною. Якщо універсальну множину задати характеристичною властивістю Q:
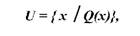
то множини А, В, С що є частинами універсальної множини и визначаються властивостями відповідно :
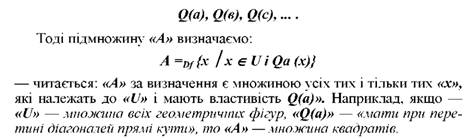
Якщо властивості, якими задані деяка множина і її підмножини співпадають, то ці множини будуть рівні. У цьому випадку говорять, що множина є частиною самої себе, або повною частиною. А у тому випадку, якщо властивість, якою задається деяка підмножина суперечить властивості за допомогою якої задана сама множина, то така підмножина буде порожньою. Тому порожня підмножина є частиною будь-якої множини, її ще називають "порожньою частиною".
Повна і порожня частини називаються невласними підмножинами. Решта підмножин є власними.
За формулою 2n можна вирахувати кількість підмножин будь-якої множини. (2 вказує на кількість невласних підмножин: саму множину, як частину самої себе; і порожню множину θ, а п - число елементів, що входить у множину. Наприклад, маємо множину "А" із трьох елементів (1, 2, 3}. Застосуємо формулу 2n для визначення кількості підмножин цієї множини: 23 = 8. Запишемо всі підмножини множини "А":

Відношення включення буває двох видів:
а) включення в широкому смислі, і
б) включення у вузькому смислі.
"А" включається у "В" в широкому смислі тоді і тільки тоді, коли "А" включається у "В" і не виключено, що "А = В". Ця ситуація записується так:
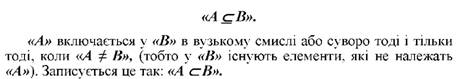
Як уже зазначалося, зміст поняття відображає властивості предметів або відношення між ними. Коли предмет позначити через "х", а його властивість через "Q", то обсягом поняття буде множина, кожний елемент якої будучи підставлений на місце "х" у формулі "Q(х)" даватиме істинне судження.
Наприклад, нехай у формулі "Q(х)" - Q - представляє властивість "бути планетою", тоді замість "х" можна підставити імена предметів: "Земля", "Марс", "Юпітер", тощо, і при цьому отримаємо істинні судження ("Земля - планета", "Марс - планета", "Юпітер - планета" тощо).
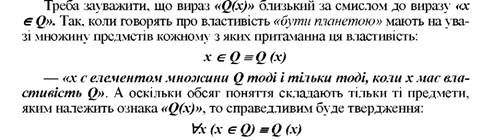
- "кожний предмет такий, що коли він є елементом обсягу поняття, то йому належить ознака, що складає зміст цього поняття".
Якщо врахувати все це і звернутися до понятійної функції, то стає очевидним, що обсягом поняття є значення понятійної функції:
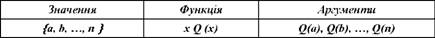

7. Види понять
8. Зміст поняття та склад злочину.
9. Логічні відношення між поняттями.
10. Логічні операції над поняттями
Види дефініцій.
Розділ IX. Судження
1. Загальна характеристика судження
2. Судження і речення
3. Види суджень. Атрибутивні судження