Логіка - Конверський А.Є. - Види дефініцій.

У формулюванні визначення як логічної операції (яке наводилось вище) можна виділити два основних завдання, які вирішує ця операція:

по-перше, відшукує, будує який-небудь предмет, вирізняє його серед інших предметів;

по-друге, формує значення для терміну, який вводиться вперше у комунікативний процес або уточнює значення уже вживаного терміну.

Залежно від цих завдань усю множину дефініцій поділяють на дві підмножини:

а) реальні дефініції і

б) номінальні дефініції.

Р е а л ь н о ю дефініцією називається визначення, яке ототожнює, розрізняє, будує, виділяє предмет. Іншими словами, реальна дефініція визначає предмет.

Н о м і н а л ь н о ю дефініцією називається визначення, за допомогою якого розкривається, уточнюється, вводиться значення термінів. Назва номінального визначення походить від латинського слова - nomina (ім'я).

Як уже зазначалося, визначення - це детермінація смислу і значення одного терміну Dfd через смисл і значення другого терміну Dfn. Хоча кажуть, що визначення (реальне) як логічна операція розкриває предмет, але усвідомлюють те, що Dfd це завжди термін, тобто послідовність знаків (природної чи штучної мови).

Тому не зважаючи на розподіл всієї множини дефініцій на реальні і номінальні стосовно тих завдань, які ці дефініції вирішують, до поділу дефініцій на реальні і номінальні, можна підійти ще й з того боку, яку функцію виконує у дефініції Dfd як знакове утворення.

Dfd як знак може виконувати дві функції:

а) репрезентативну (тобто, представляти об'єкти позамовного характеру), і

б) номінативну (тобто функцію іменування або згадування).

Якщо Dfd виконує репрезентативну функцію, то мають реальне визначення, а якщо номінативну функцію, то - номінальне визначення. Оскільки у реальному визначенні Dfd представляє об'єкти позамовного характеру, то тут Dfd належить до виразів об'єктної мови. Фактично у реальних дефініціях Dfd виконує роль замінника того об'єкту, який він представляє як знак. У цьому розумінні цілком справедливо визначати пізнавальну мету реальних дефініцій як таку, що визначає предмети і явища дійсності, які зафіксо-

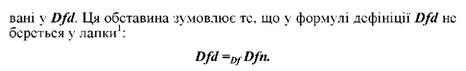
Виходить у реальних дефініціях В/й не може належати до категорії термів (імен: індивідів, властивостей, відношень, класів, висловлювань). А оскільки відомо, що у ролі логічного присудка може вживатися тільки предикатор (загальне ім'я або висловлювання), то і В/н теж не може належати до категорії термів. Наприклад,

1. Париж - столиця Франції.

2. Столиця Франції - Париж.

3. Планети Сонячної системи - це космічні тіла, які обертаються навколо Сонця.

4. Лінія є діаметром тоді і тільки тоді, коли це відрізок прямої, що проходить через центр кола.

У прикладах 1, 2, 3 Dfd належить до категорії предикаторів, а у прикладі 4 до категорії висловлювань. Dfd у 1 і 2 прикладах представляють одиничні класи, а не окремі елементи. Отже, взаємозамінюваність Dfn на Dfd у реальних дефініціях означає, що вони тотожні як об'єкти однієї семантичної категорії (предикатори).

Як уже зазначалося у номінальних дефініціях Dfd вживається у функції іменування. А це означає, що у цих дефініціях Dfd належить до метамови. Якщо у реальних дефініціях Dfd - у функції репрезентації говорить про предмет, то у номінальних дефініціях Dfd у функції іменування говорить про слово. Наприклад:

1. "Париж" - складається із п'яти букв.

2. Слово "Париж" - чоловічого роду.

3. "Марс" - термін, який позначає планету Сонячної системи.

4. Вираз "автор Кобзаря" - описове ім'я.

Очевидно, що у наведених прикладах Dfd у номінальних дефініціях завжди є термом, а В/н може бути у репрезентативній функції:

1. "Dfd" =Df "Dfn"

2. "Dfd" =Df Dfn.

Перша формула відповідає дефініції: "Борисфен" означає теж саме, що і "Дніпро". Друга - відповідає дефініції: "Словом "геометрична фігура" називають трикутники, квадрати, трапеції тощо".

Після загальних зауважень щодо поділу дефініцій на реальні і номінальні розглянемо конкретні види реальних і номінальних визначень.

До реальних визначень належать:

1. Визначення через рід і найближчу видову відмінність;

2. Визначення через вказівку на протилежність;

3. Генетичне визначення;

4. Операціональне визначення;

5. Індуктивне визначення.

Суть дефініції через рід і видову відмінність полягає в тому, що спочатку знаходять найближче родове поняття для В/й, а потім перераховують характерні видові відмінності.

Наприклад, "Республіка - це форма правління, при якій всі вищі органи державної влади вибираються народом, або формуються загальнонаціональними представницькими установами"; "Автократія - це монархія в якій відсутні справжні представницькі установи" і т.д. Цей вид визначення є найбільш поширеним.

Якщо потрібно дати визначення універсальним поняттям, а саме категоріям філософії, то тут дефініція через рід і видову відмінність малоефективна. У цих випадках застосовують дефініцію через вказівку на протилежність. Наприклад, "Випадковість - це форма прояву і доповненння необхідності"; "Форма - це спосіб існування змісту" і т.д.

Наступним видом реального визначення є генетична дефініція. Г е н е т и ч н и м визначенням називається така реальна дефініція, у якій фіксуються способи походження і побудови визначуваного предмета. Генетичні дефініції широко застосовуються у математиці, фізиці, хімії тощо. Наприклад, "Коло - це частина площини, обмеженої замкненою лінією, яку отримують у результаті руху точки на цій площині на однаковій відстані від центру"; "Куля - це тіло, яке утворюється обертанням півкола навколо діаметра" тощо. Даний вид визначення застосовують в геометрії, фізиці і т.д.

Операціональна дефініція розповсюджена в експериментальних науках. О п ер а ц і о н а л ь н и м визначенням називається такий вид реальної дефініції, який полягає у описові специфічних експериментальних операцій для знаходження тих чи інших об'єктів. Наприклад, "Луг - це хімічна речовина, яка зафарбовує лакмусовий папірець у синій колір"; "Ять-мідянка - зелена фарба, яка отримується шляхом окислення міді".

До реальних дефініцій належить індуктивне визначення.

Індуктивним визначенням є процедура, яка передбачає:

1) явну вказівку на вихідні елементи (вони або повністю перераховуються, або дається критерій, за яким можна виділити їх із певної множини);

2) правила утворення із вихідних елементів похідних;

3) обмеження, яке вказує, що окрім наведених в 1 і утворених відповідно до 2 немає ніяких інших, які б належали множині, що визначається.

Даний вид дефініцій має розповсюдження в математиці, сучасній логіці.

Візьмемо для прикладу дефініцію формули у мові класичної логіки висловлювань:

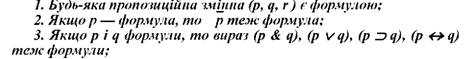
4. Ніщо крім виразів перерахованих в 1, 2, 3 не є формулою у мові класичного числення висловлювань.

Номінальні дефініції поділяються на синтаксичні і семантичні, а семантичні - на аналітичні і синтетичні.

С и н т а к с и ч н и м називається визначення у якому вказується як можна замінити знаки або їх сполучення іншими (як правило коротшими), не звертаючи уваги на їх значення. Синтаксичним визначенням буде дефініція операції об'єднання множин:

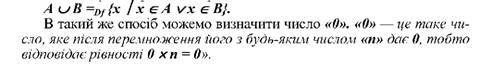
Граматичні знаки, коми, крапки, дужки тощо, також визначаються синтаксично.

С е м а н т и ч н и м називається визначення, яке певному позначенню ставить у відповідність предмет, охарактеризований через його відмінні ознаки.

Наприклад, "Слово "п'ятикутник" означає багатокутник з п'ятьма сторонами". Особливістю семантичних визначень є те, що у них у правій частині говориться про предмет, а у лівій - про термін. Вони відповідають формулі: "Dfd" =Df Dfn.

З наведеної формули видно, що до Dfd і Dfn не можна застосовувати вимогу взаємозамінюваності. Щоб застосувати до цього виду дефініцій правило взаємозамінюваності необхідно його перевести або у реальне, або у номінальне несемантичне визначення. Наприклад, маємо семантичну дефініцію "Слово "квадрат" означає прямокутник з рівними сторонами" - "В/й" =В/ В/п.

Його можна перетворити на реальне визначення: "Квадрат - це прямокутник з рівними сторонами" - Dfd =Df Dfn, або у номінальне

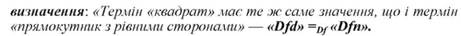
Семантичні визначення, як уже зазначалося, мають дві підмножини:

- аналітичні визначення і

- синтетичні визначення.

А н а л і т и ч н и м визначенням називається такий вид семантичних дефініцій, який розкриває значення термінів, що уже існують у даній мові. Прикладами аналітичних визначень є визначення слів, що входять до тлумачних словників. Формою аналітичного визначення може бути вираз: "Під терміном Т у науці N розуміють ...". Наприклад, "під терміном "нормативний акт" у юридичній практиці розуміють правовий акт держави, у якому містяться накази - норми права, що регулюють суспільні відносини певного виду".

Аналітичні визначення вживають особливо тоді, коли один і той самий термін у різних науках вживається у різному значенні.

С и н т е т и ч н и м визначенням називається такий вид семантичних дефініцій, який розкриває значення терміну що вперше вводиться, або уточнює значення терміну, який уже наявний у даній мові. Прикладами синтетичних визначень будуть визначення вперше введених термінів: "правова держава", "ринкова економіка", "харизма", "креатив" тощо.

В залежності від того, який характер має визначуване поняття, дефініції поділяються на явні та неявні.

Явною дефініцією є таке визначення, в якому визначуване представляє предмет або явище у вигляді сукупності суттєвих ознак. Іншими словами, у явних визначеннях завжди за визначуваним поняттям стоїть реально існуючий предмет, явище або термін, який їх позначає.

Неявною дефініцією є визначення, в якому визначуване стає зрозумілим із контексту.

До основних видів явних визначень відносять: визначення через найближчий рід та видову відмінність, генетичне визначення, визначення через вказівку на протилежність, операціональне.

Видами неявних визначень є: контекстуальне, індуктивне, аксіоматичне.

Контекстуальними визначеннями є визначення, в яких визначуване поняття пояснюється, розкривається через відношення термінів контексту.

Прикладами контекстуальних визначень є визначення службових слів у граматиці, "sin", "cos", ">" в математиці і т.д.

Індуктивний визначенням є дефініція, яка дозволяє із сукупності вихідних об'єктів за допомогою спеціальних операцій утворювати нові об'єкти. За допомогою індуктивних визначень здійснюють визначення натурального числа в математиці, формули в сучасній логіці.

Аксіоматичним визначенням називається дефініція, яка розкриває значення вихідних понять теоріях на основі фундаментальних властивостей аксіом.

Операція визначення поняття підпорядковується спеціальним правилам.

1. Визначення має бути співмірним.

Це означає, що обсяги визначуваного в визначаючого поняття повинні вичерпувати один одного і мати один і той же зміст.

Наприклад, у визначенні: "Злочин - це суспільно небезпечне діяння, яке вчинене суб'єктом злочину" і визначуване поняття "Злочин" (А) і визначаюче "суспільно небезпечне діяння, яке вчинене суб'єктом злочину" (В) співпадають, є тотожними, вказують на одне і те ж явище.

Це видно і на даній схемі.

Прикладами співмірних визначень є: "Історія - це наука, що досліджує минуле суспільства з метою адекватної оцінки сучасного стану суспільства та визначення перспектив розвитку суспільства у майбутньому"; "Парламент - це загальнонаціональний представницький орган державної влади, що діє постійно і творить закони"; "Папство - релігійний монархічний центр католицької церкви, який очолює Папа Римський"; "Монархія - форма правління, за якої державна влада зосереджена в руках одноосібного глави держави - монарха і спадково передається" і т.д.

При порушенні цього правила виникають логічні помилки:

а) занадто широке визначення;

б) занадто вузьке визначення.

Суть логічної помилки "занадто широке визначення" полягає в тому, що в процесі визначення через найближчий рід та видову відмінність береться не специфічна видова ознака виду, що визначається, а ознака, яка властива й іншим видам даного роду. Внаслідок цієї помилки обсяг визначаючого поняття є більшим від обсягу визначуваного поняття.

Визначеннями, які містять дану помилку, будуть наступні: "Шахрайство - заволодіння чужим майном"; "Історія - наука про людське суспільство"; "Монархія - форма правління державою" і т.д.

Наступною помилкою при порушенні цього правила є "занадто вузьке визначення". Суть цієї помилки полягає в тому, що в процесі визначення обирається не видова ознака, а ознака, яка належить підвидові або індивідові. Це приводить до того, що обсяг визначаючого поняття є вужчим від обсягу визначуваного поняття.

Прикладами визначень, які будуть "занадто вузькими" є: "Адвокат - це особа, яка виступає в суді захисником у цивільних справах"; "Шахрайство - це заволодіння сусідським майном шляхом обману"; "Історія - це наука про виникнення, існування, розвиток античного суспільства" і т.д.

2. Визначення не повинно утримувати в собі кола.

Дане правило вимагає, щоб поняття не визначалося саме через себе.

При порушенні цього правила виникає логічна помилка "хибне коло". Ця помилка має два різновиди:

а) "коло у визначенні" і

б) "тавтологія".

Суть помилки "коло у визначенні" полягає в тому, що в процесі визначення на роль визначаючого поняття беруть поняття, яке визначається за допомогою першого.

Прикладами визначень, які утримують помилку "коло у визначенні" є наступні: "Кримінальне право регулює відносини, які передбачені кримінальним кодексом"; "Логіка - наука про правильне мислення"; "Історія - це наука про історичні явища"; "Монархія - це правління державою монархом" і т.д.

Другим різновидом помилки "коло у визначенні" є помилка "тавтологія" (або "тавтологічне визначення").

Тавтологія теж утворює коло у визначенні, але в більш вираженій формі. Це відбувається завдяки тому, що визначаюче поняття більш виражене, більш буквально повторює визначуване поняття.

Наприклад, "Кримінальне право - це наука про кримінальне право"; "Логіка - це наука про логічне мислення"; "Історія - це наука про історію"; "Монархія - це монархічна держава" і т.д.

Логічну помилку "тавтологія у визначенні" не слід змішувати з такими виразами: "історія є історія", "держава є держава", "закон є закон", "факт є факт" і т.д.

Перераховані вирази не є визначеннями. Наприклад, вираз "факт є факт" не є дефініцією, в ньому лише стверджується, що факт є фактом і тому до нього слід підходити як до факту, сприймати його з урахуванням усіх його суттєвих ознак, усіх проявів і модифікацій, і поза цим поняття факт мислити не можна.

3. Визначення за можливості не повинно бути заперечувальним. Це правило передбачає основне завдання дефініції - розкрити, які

суттєві ознаки входять до змісту визначуваного поняття. Іншими словами, в ході визначення відбувається констатація суттєвих ознак, що складають зміст визначуваного поняття.

В заперечувальному визначенні фіксується лише відсутність ознак у змісті визначуваного поняття і не вказується, які ознаки повинні складати зміст визначуваного поняття.

Наступні вирази не є дефініціями: "Крадіжка - це не грабіж"; "Суддя - це не адвокат"; "Історія - це не географія"; "Республіка - це не монархія" і т.д.

Ці вирази зовні схожі на визначення, але визначеннями не є. Вони не розкривають зміст визначуваного поняття.

Слід зазначити, що вимога, яка міститься в цьому правилі, не є універсальною. Бувають випадки, коли для предметів і явищ важливим, суттєвим є не наявність певних ознак, а їх відсутність. В цих випадках застосовують заперечу вальну форму визначення.

Як правило, ці визначення найбільш поширені в геометрії, математиці, сучасній логіці і т.д.

Наприклад, "Паралельними лініями є лінії, які ніколи не перетинаються"; "Непарним називається число, яке не ділиться на 2".

4. В процесі визначення не можна використовувати метафори, порівняння, різноманітні літературні прийоми.

Метафори, порівняння широко використовуються в практиці міркування, у спілкуванні, вони роблять певні ознаки предметів та явищ більш мальовничими, привабливими, але при цьому, і це саме головне, вони не можуть відобразити, представити суть ознак, що складають зміст поняття. Тому такі прийоми не є науковими дефініціями.

Застосовуючи метафори, порівняння, різноманітні літературні прийоми, ми робимо нашу мову живою, барвистою, образною, такою, що сприяє глибшому взаєморозумінню. І все ж таки, слід пам'ятати, що такі прийоми не мають нічого спільного з логічною операцією визначення поняття.

Наприклад, "Скрипка - це королева оркестру", "Закон - це меч правосуддя", "Совість - це внутрішній суддя", "Архітектура - це музика, втілена в камені" і т.д.

Кожен з наведених прикладів свідчить про те, що з їх допомогою не можна відрізнити визначуваний предмет від схожих з ним, не можна виділити сутність предмету, що представлений у визначуваному понятті. Тут лише своєрідним чином акцентується, звертається увага на одну ознаку предмету, важливу в деякому відношенні.

Чітке дотримання описаних правил гарантує відсутність помилок в здійсненні операції визначення поняття і забезпечує ясність, послідовність, несуперечливість наших міркувань в цілому.

Дотримання перерахованих правил допомагає формулювати ясні, правильні визначення, які допомагають збагнути свої власні знання і передати ці знання іншим у ясній і доступній формі.

Окрім логічної операції визначення поняття у практиці міркувань широко використовуються процедури, які подібні до визначення, але такими не є. Зокрема, це такі процедури як:

- опис,

- характеристика,

- порівняння, - розрізнення,

- остенсивне визначення.

О п и с о м називається процедура, яка полягає у перерахуванні ознак, які більшою або меншою мірою розкривають певний предмет.

Опис застосовують при оцінці місця злочину чи пригоди, місцевості, виду рослин чи тварин тощо.

Наприклад, "Тигр - це ссавець родини котячих, один з найбільш великих сучасних хижих звірів. Голова округлої форми, з короткими вухами і боками, червонувато-рудуватим забарвленням, з чорними поперечними смугами".

X а р а к т е р и с т и к о ю називається прийом, за допомогою якого вказують якісь помітні ознаки предмету, важливі у певному відношенні. Характеристика може бути повною або неповною, позитивною або негативною, всебічною або односторонньою, але вона повинна завжди бути об'єктивною. Іноді характеристика може мати лише одну ознаку. Наприклад, "Ньютон - геніальний фізик".

П о р і в н я н н я м називається процедура ознайомлення з предметом, коли визначення неможливе або не потрібне. Порівняння, власне, є способом пояснення специфіки предметів через аналогію і, головним чином, через метафори.

Наприклад, "Природа - Вчитель людини", "Столиця - серце держави", "Бавовна - біле золото" тощо.

Р о з р і з н е н н я - це прийом, за допомогою якого відрізняють один предмет від інших, схожих з ним предметів.

Прикладом розрізнення може бути фіксація особливих прикмет при розшуку людей чи зниклих речей.

Ос т е н с и в н и м визначенням називається процедура, яка полягає в демонстрації предмета (у вказівці на предмет).

Наприклад, коли демонструють предмет і називають його "Це будинок", "Це телевізор".

Отже, логічна операція визначення поняття виконує важливу функцію у наукових дослідженнях і практиці міркування. За допомогою дефініції підсумовують знання про предмет, полегшують пошук предмета, який становить дослідницький чи практичний інтерес, розкривають значення термінів, і, нарешті, дефініція є важливим засобом скорочення складних описів, засобом скорочення окремих міркувань у наукових теоріях.

Контрольні запитання та вправи

І

1. Характеристика індивіду як предмета думки.

2. Характер абстрагування, що має місце при утворенні терму.

3. Суть ототожнююче - відрізняючого абстрагування.

4. Мовні засоби вираження поняття.

5. Види ознак предмета думки.

6. Дефініція змісту поняття.

7. Предикат як знакова форма фіксації змісту поняття.

8. Типологія ознак за субстанціональністю.

9. Родові та видові ознаки.

10. Дефініція обсягу поняття.

11. Обсяг поняття як множина.

12. Поняття множини.

13. Характеристика відношень: "належність елемента множині" і "включення множини в множину".

14. Поняття "універсальної множини", "повної підмножини", "порожньої множини".

15. Способи задання множин.

16. Процедура вирахування кількості підмножин будь-якої множини.

17. Обсяг поняття як значення понятійної функції.

18. Обґрунтування закону оберненого відношення між змістом та обсягом поняття.

19. Типологія видів понять.

20. Логічні відношення між сумісними поняттями.

21. Логічні відношення між несумісними поняттями.

22. Обмеження та узагальнення понять.

23. Операція доповнення обсягу поняття.

24. Операція перетину обсягів поняття.

25. Операція об'єднання обсягів поняття.

26. Здійснення операції перетину над сумісними поняттями.

27. Здійснення операції об'єднання над сумісними та несумісними поняттями.

28. Різниця обсягів понять.

29. Структура операції поділу понять.

30. Види поділу понять.

31. Правила поділу понять та можливі помилки при їх порушенні.

32. Природна та штучна класифікація.

33. Розчленування цілого на частини.

34. Види визначення.

35. Структура операції визначення понять.

36. Синтаксична та семантична площини аналізу дефініції.

37. Прагматичний аспект дефініції.

38. Види реальних дефініцій.

39. Види номінальних дефініцій.

40. Правила визначення.

41. Процедури, подібні до визначення поняття.

ІІ

1. Дайте логічний аналіз перерахованих понять: "юридична особа", "неуспішність", "роман Л.М.Толстого", "футбольна команда", "метал, який не проводить електричний струм", "центральне тіло Сонячної системи", "кредитор".

2. Встановіть обсяг таких понять: "основні формально-логічні закони", "місто", "держава", "справедливість", "наукова бібліотека".

3. Наведіть приклади збірних понять.

4. Які пари предметів увійдуть до обсягу понять: "ровесник", "учитель", "брат", "столиця".

5. Які з наведених предикатів є одномісними, двомісними, тримісними: "талановитий", "сестра", "знаходитися між".

6. Наведіть приклади синонімів та омонімів.

7. Наведіть приклади понять які б знаходилися у відношенні тотожності з такими поняттями: "квадрат", "адміністративний, економічний, культурний центр держави", "злочин", "підручник".

8. Зобразіть у вигляді колових схем відношення між такими поняттями:

а) "військовослужбовець", "капітан", "полковник", "викладач";

б) "юрист", "депутат", "лауреат";

в) "чотирикутник", "паралелограм", "ромб", "квадрат", "прямокутник".

9. Знайдіть поняття, обсяг якого частково співпадає з обсягом даного: "лікар", "метал", "європейська держава", "учень".

10. Чи правильно здійснено поділ понять:

а) картини бувають історичні і пейзажні;

б) клімат буває холодний, помірний, жаркий, морський і континентальний;

в) науки поділяють на гуманітарні, природничі, технічні і біологічні.

11. Чи правильно здійснено визначення таких понять? Якщо ні, то які правила порушені:

а) фізика - це наука про фізичні явища;

б) логіка - це наука про мислення;

в) географія - це геологія;

г) демократ - це людина, яка дотримується демократичних поглядів;

д) планета - це космічний об'єкт на якому існує життя.

12. Наведіть приклади номінальних дефініцій і переформулюйте їх у реальні.