Логіка - Конверський А.Є. - 1. Загальна характеристика умовиводу

1. Загальна характеристика умовиводу

Серед мислиннєвих операцій важливе місце займає умовивід. На відміну від поняття та судження умовивід є логічною операцією, завдяки якій із однієї або декількох думок виводять нову думку. Можна навести й таке визначення умовиводу:

Ум о в и в о д о м називається така форма мислення, за допомогою якої із одного або декількох відомих суджень отримують нове судження.

Умовивід складається із:

- засновків та

- висновку.

З а с н о в к а м и називаються раніше відомі судження, на підставі яких робиться висновок.

В и с н о в к о м називається нове судження, отримане в результаті співставленая засновків.

Наприклад,

1. Будь-який обвинувачуваний має право на захист.

2. Мій приятель є обвинувачуваним.

3. Отже, мій приятель має право на захист.

1 і 2 судження будуть засновками, а 3 судження - висновком.

Процес отримання нової думки (надалі - виведення), базується на певних правилах та законах логіки. Тому виведення в умовиводі носить закономірний характер. Це зумовлює таку особливість умовиводу, на відміну від поняття і судження, що він характеризується не адекватністю, істинністю або хибністю, а правильністю чи неправильністю.

Всю множину умовиводів за характером зв'язку між засновками та висновком поділяють на:

- дедуктивні та

- індуктивні.

Назва "дедуктивний умовивід" походить від латинського слова deductio (виведення).

У дедуктивних умовиводах між засновками та висновком існує відношення логічного слідування.

А назва "індуктивні умовиводи" походить від латинського слова inductio (наведення).

В індуктивних умовиводах між засновками та висновком існує відношення наведення.

У традиційній логіці умовиводи за напрямком виведення наслідку поділяються на дедуктивні, індуктивні.

У дедуктивному умовиводі ми переходимо від загального до часткового, або одиничного; в індуктивному - від одиничного до загального.

За ступенем обґрунтованості висновку умовиводи поділяють на:

- демонстративні та

- правдоподібні (імовірні).

У демонстративних умовиводах висновок необхідно істинний, а в правдоподібних - імовірно істинний.

За кількістю засновків умовиводи поділяються на

- безпосередні та

- опосередковані.

Б е з п о с е р е д н і м умовиводом називається такий умовивід, в якому висновок отримують із одного засновку.

О п о с е р е д к о в а н и м умовиводом називається такий умовивід, в якому висновок отримують із двох і більше засновків.

В залежності від того, чи випливає висновок із засновків з урахуванням логічної структури засновків, чи ні, умовиводи поділяються на силогізми та умовиводи логіки суджень.

2. Умовиводи логіки суджень

Зупинимося на аналізі дедуктивних умовиводів, а саме на характеристиці умовиводів логіки суджень.

Для цього класу умовиводів характерним є те, що в них при отриманні висновку не враховується внутрішня структура простих суджень, із яких складаються засновки і висновок. Тут отримання висновку базується тільки на смислі логічних сполучників.

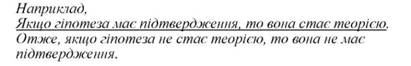
Логічна структура такого міркування має такий вигляд:

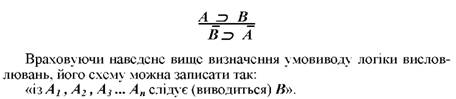
Цей вираз розуміється так: "Якщо істинні висловлювання із структурою заданою формулами А1, А2 , А3, ... А" (засновки), то істинним є і висловлювання із структурою, заданою формулою В (висновок)".

З даного визначення видно, що ми відволікаємося від змісту висловлювань і зосереджуємо увагу на структурі засновків і висновку.

Надалі схему висновку із засновками А1, А2, А3... А" і наслідком В будемо записувати так:

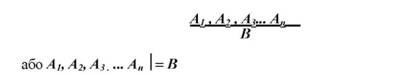
Вважається, що ця схема припустима, а висновок є правильним тоді і тільки тоді, коли кон'юнкція засновків, що сполучена з висновком знаком імплікації є тотожно-істинною формулою (тавтологією) логіки

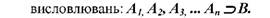
Треба зауважити, що у правильному висновку між кон'юнкцією засновків і висновком існує відношення логічного слідування. У тому випадку, коли знайдеться хоча б один набір значень змінних, що вхо-

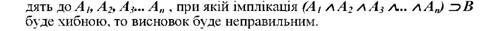
Необхідно мати на увазі: 1. Правильність міркування сама по собі не гарантує істинність висновку. Істинність всіх засновків правильного висновку є лише достатньою умовою істинності висновку, але якщо хоча б один із засновків є хибним, то висновок може бути будь-яким:

2. Істинність висновку не означає правильність умовиводу, оскільки істинність висновку не є ні достатньою, ні необхідною умовою правильності умовиводу.