Логіка - Мозгова Н.Г. - 3. Правила засновків силогізму

З істинних засновків не завжди можна отримати істинні висновки. Для його істинності необхідно ще дотримання загальних правил категоричного силогізму. Існують сім загальних правил силогізму: три З них відносяться до термінів і чотири - до засновків. Розглянемо правила термінів силогізму:

1) У даному силогізмі повинно бути тільки три терміни. Вивід в силогізмі грунтується на відношенні двох крайніх термінів, тому він повинен мати тільки три терміни. Порушення цього правила пов'язане з явищем багатозначності слів, коли середній термін в одному засновку має одне значення, а в іншому - інше значення. Така помилка є порушенням вимог закону тотожності і називається подвоєнням терміна.

Наприклад:

Штамп (М) є технологічна оснастка (Р). Це судження (Б) є штампом (М).

Це судження (8) є технологічною оснасткою (Р)?!

У другому засновку під словом "штамп" розуміють вираз, який перетворився на загальне, позбавлене смислу твердження. У результаті порушення зв'язку між крайніми термінами виникає позбавлений змісту висновок.

2) Середній термін повинен бути розподіленим принаймні в одному із засновків. Якщо середній термін (М) не розподілений у жодному із засновків, то зв'язок між крайніми термінами буде невизначеним. Наприклад:

Деякі студенти (М) - відмінники (Р). Усі мої друзі (5) - студенти (М). 777

1-ший засновок:

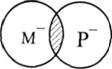
М-нерозподілений у жодному із засновків. 2-гий засновок:

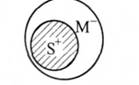
Висновок може бути:

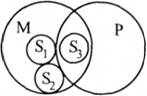
a) Усі мої друзі - відмінники.

b) Деякі з моїх друзів - відмінники.

c) Жоден з моїх друзів не є відмінником.

3) Якщо крайній термін (8, Р) не розподілений у засновку, то він не повинен бути розподілений і в висновку (і навпаки). Наприклад: Усі мої друзі (М) - студенти (Р). Симоненко (Бї не є моїм другом (МУ Симоненко (8) не є студентом (Р)?! 1 - ший засновок

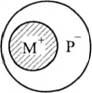
Р" - у засновку. 2-гий засновок

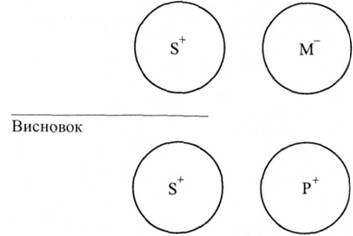
Р+ - у висновку.

Висновок не є необхідним і не може вважатися істинним. Помилка пов'язана з порушенням правила розподіленості крайніх термінів.

3. Правила засновків силогізму

1) Принаймні один із засновків силогізму повинен бути стверджувальним судженням. З двох заперечних суджень висновок з необхідністю не витікає. Наприклад:

Серед студентів університету "Україна" (М) немає математиків (Р).

Серед студентів КДУ ($) немає студентів університету "Україна" ПУГ).

Оскільки обоє засновків є заперечними,

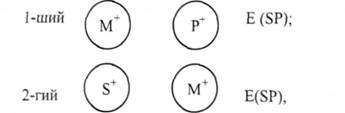
то відношення між Б та Р є невизначеним. Тут можливі такі твердження: Е(5Р) - "Жоден студент КДУ не є математиком", О (БР) - "Деякі студенти КДУ не є математиками", А (5Р) - "Усі студенти КДУ є математиками".

2) Якщо один із засновків - заперечне твердження, то і висновок повинен бути заперечним. Наприклад:

Зацікавлений суддя (М) не бере участі в розгляді справи (Р). Сидоренко (Б) є зацікавленим суддею (М).

Сидоренко (Б) не бере участі в розгляді справи (Р).

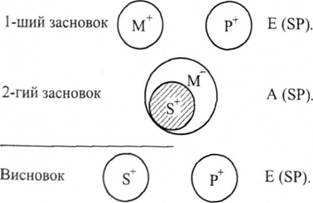
Оскільки всі Б належать до М, а жодне М не належить до Р, то жодне в не належить до Р. Висновок є загальнозаперечним судженням.

3) Принаймні один із засновників повинен бути загальним судженням. Із двох часткових суджень висновок з необхідністю не витікає. Наприклад:

Деякі філателісти - адвокати І (БР). Деякі прокурори - філателісти І (БРУ ? ? ?

4) Якщо один із засновків - часткове судження, то висновок повинен бути частковим.

Усі студенти-юристи (М) вивчають логіку (Р) А (БР). Деякі слідчі (5) є студентами-юристами (М) І (БРУ Деякі слідчі (Б) вивчають логіку (Р) І (5Р). Оскільки менший засновок цього силогізму є частковим судженням І (БР), то і висновок його є частковим судженням І (БР).

4. Фігури та модуси силогізму

У засновках простого категоричного силогізму середній термін (М) може займати місце суб'єкта (Б) або предиката (Р). У залежності від цього розрізняють чотири різновиди силогізму, які називають його фігурами:

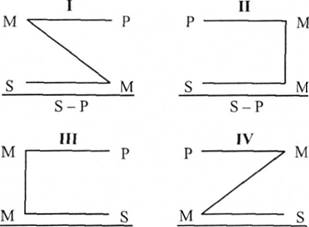
Б-Р 5-Р

У І-шій фігурі середній термін займає місце суб'єкта в більшому засновку і місце предиката в меншому засновку. У ІІ-гій фігурі - місце предиката в обох засновках. У Ш-тій фігурі — місце суб'єкта в обох засновках.

У IV-тій фігурі - місце предиката в більшому засновку і місце суб'єкта в меншому засновку.

Ці фігури вичерпують усі можливі комбінації термінів силогізму.

Таким чином *фігури силогізму - це його різновиди, які відрізняються місцем середнього терміну в засновках.

Засновками силогізму можуть бути категоричні судження, різні за якістю та кількістю: А, Е, 1, О. Число можливих комбінацій двох засновків в одній фігурі силогізму дорівнює 24 = 16:

АА ЕА ЇА ОА

АЕ (ЕЕ) IE (ОЕ)

AI EI (II) (Ol)

AO (EO) (10) (00).

Отже, в чотирьох фігурах силогізму всіх можливих модусів буде 16 х 4 = 64. Але не всі ці можливі комбінації засновків відповідають вимогам загальних правил силогізму. Так, наприклад, у наведених 16-ти комбінаціях для однієї фігури не відповідають правилам засновків такі: ЕЕ, ЕО, ОЕ, 00 — вони обидва є заперечними; II, 10, 01 — вони обидва є частковими. Такі комбінації засновків слід виключати.

Врахувавши вимоги всіх загальних правил силогізму, з 64-х можливих модусів силогізму отримаємо 19 правильних, або сильних його модусів. Дописавши тип судження-висновка отримаємо:

І-ша фігура: ААА, EAE, AH, ЕІО.

ІІ-га фігура: EAE, АЕЕ, ЕІО, АОО.

Ш-тя фігура: А AI, 1 AI, All, ЕАО, ОАО, ЕІО.

IV-та фігура: ААІ, АЕЕ, ІАІ, ЕАО, ЕІО.

* Різновиди силогізму, що розрізняються якістю та кількістю засновків та висновку, називаються модусами (від латинського modus - спосіб, образ) простого категоричного силогізму.

Правильними, або сильними серед них є такі, що відповідають усім вимогам загальних правил силогізму. Сильних модусів - 19.

Крім сильних модусів існують і слабкі модуси, тобто такі, що дають необхідний вивід при певних умовах.

Неважко помітити, що серед сильних модусів є видимі повтори. Наприклад, модус ЕАЕ в І-шій фігурі і модус ЕАЕ - у ІІ-гій. Не слід забувати, що ці модуси належать до різних фігур силогізму і крім типів суджень засновків та висновку (А, Е) розрізняються ще місцем середнього терміна. Таким чином, це - неоднакові силогізми.