Оскільки середній термін силогізму (М) займає в кожній з чотирьох фігур різне місце, то кожна фігура має свої особливі правила, які виводяться з загальних правил силогізму.
Правила І-шої фігури.
1. Більший засновок є загальним судженням (А, або Е).
2. Менший засновок є стверджувальним судженням (А, або І).
Перша фігура є найбільш типовою формою дедуктивного умовиводу. У ній із загального твердження, яке є законом науки чи правовою нормою, робиться висновок про окремий факт, одиничний випадок чи частину предметів даного класу. Широко використовується ця фігура силогізму в різних сферах пізнавальної та практичної діяльності.
Наприклад:
Усі метали (М) є електропровідними (Р). Мідь (S) - метал (М). Мідь (S) є електропровідною (Р).
Правила ІІ-гої фігури.
1. Більший засновок - загальне судження (А, Е).
2. Один із засновків - заперечне судження (Е, О).
Друга фігура силогізму застосовується тоді, коли необхідно показати, що окремий випадок (конкретна особа, факт, подія тощо) чи частина предметів даного класу не відповідає загальному твердженню. Але друга фігура силогізму стверджувальних висновків не дає. Наприклад:
Усі видатні шахісти (Р) знають теорію шахової гри (М). Савчук (5) не знає теорії шахової гри (М). Савчук (Б) не є видатним шахістом (Р).
Правила ІІІ-тьої фігури.
1. Менший засновок - стверджувальне судження (А, І).
2. Висновок - часткове судження (І, О).
Оскільки третя фігура загальних висновків не дає, то вона використовується в тих випадках, коли необхідно ствердити або заперечити деякі ознаки відносно частини предметів даного класу. Наприклад:
Деякі депутати (М) - юристи (Р).
Усі депутати (М) — недоторкані особи (5).
Деякі недоторкані особи (S) - юристи (Р).
Висновки третьої фігури силогізму в практиці мислення використовуються відносно рідко.
Правила IV-тої фігури.
1. Якщо більший засновок - стверджувальне судження (А, І), то менший засновок повинен бути загальним судженням (А, Е).
2. Якщо один із засновків - заперечне судження (Е, О), то більший засновок повинен бути загальним судженням (А, Е). Наприклад:
Усі кити (Р) - ссавці (М).
Жоден ссавець (М) не є рибою (S)
Жодна риба (S) не с китом (Р).
Висновки за четвертою фігурою категоричного силогізму в практиці мислення використовуються надто рідко.
6. Категоричний силогізм з виділяючим судженням
Якщо принаймні одним із засновків категоричного силогізму є виділяюче судження, то такий силогізм є винятком із загальних правил та особливих правил фігур категоричного силогізму. Порушуючи згадані правила, такі силогізми дають необхідні виводи. Модуси таких силогізмів називають слабкими модусами, оскільки вони не завжди дають необхідні виводи, а лише за умови, що принаймні один із засновків силогізму є виділяючим судженням.
Нагадаємо, що виділяюче судження має структуру: "S і тільки S є Р", а його оберненням буде: "Усі Р є S".
Розглянемо найбільш розповсюджені випадки слабких модусів.
1) Вивід з двох часткових суджень, що порушує загальне правило засновків силогізму: "Принаймні один із засновків силогізму повинен бути загальним судженням".
Деякі адвокати (М) - депутати (Р) І (SР).
Деякі юристи (S) - адвокати (М) І (SР).
Деякі юристи (S) - депутати (Р) І (SР).
Отже, це перша фігура силогізму, а його модус - III. Серед правильних модусів першої фігури такого модусу немає, але вивід є необхідним і висновок - істинним. Проведемо аналіз засновків нашого силогізму:
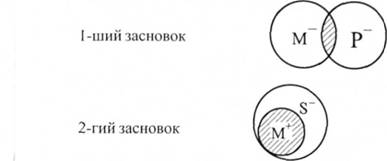
Виділяюче судження: "S і тільки S є М".
Таким чином, другий засновок (юристи і тільки юристи є адвокатами") - виділяюче судження, тому вивід є необхідним, а висновок - істинним.
2) Вивід за І-шою фігурою, коли більший засновок - часткове судження. Це порушує правило І-шої фігури: "Більший засновок повинен бути загальним судженням".
Деякі студенти (М) є дистанційниками(Р*) І(SР).
Деякі особи, що навчаються (S), є студентами (М*) І (SР).
Деякі особи, що навчаються (S'), є дистанційниками (Р) І (SР).
Це перша фігура силогізму, модус — III. Серед правильних модусів першої фігури такого модусу немає. Але оскільки обидва засновки є виділяючими судженнями, то вивід є необхідним, а висновок - істинним.
3) Вивід, у якому один із засновків - часткове судження, а висновок — загальне судження. Це порушує загальне правило засновків силогізму: "Якщо один із засновків часткове судження, то і висновок повинен бути частковим судженням".
Деякі слов'яни (Р) - українці (М+) І (SР).
Усі присутні на форумі (S*) - українці (М) А (SР).
Усі присутні на форумі (S+) — слов'яни (Р*) А(SР).
Це вивід за другою фігурою, його модус - ІАА. Такого модусу серед правильних модусів другої фігури немає. Але більший засновок є виділяючим судженням. Тому вивід є необхідним, а висновок - істинним.

4) Вивід за другою фігурою з двох стверджувальних засновків. Це порушує правило другої фігури: "Один із засновків повинен бути заперечним судженням".
Деякі історики (Р') - фахівці з історії України (М+) І (SР). Усі викладачі цієї кафедри (S+) - фахівці з історії України (М) А (SР). Усі викладачі цієї кафедри (S*) - історики (Р*) А(SР). Виділяючим у цьому силогізмі є більший засновок: "Історики і тільки історики є фахівцями з історії України".
5) Вивід за першою фігурою, в якому менший засновок — заперечне судження. Це порушує правило першої фігури: "Менший засновок повинен бути стверджувальним судженням".
Усі правильні умовиводи (М+) є необхідними (Р+) А (БР).
Цей умовивід (S+) не є правильним (М*) Е (SР).__
Цей умовивід (S+) не є необхідним (Р*) Е(SР).
Модус цього силогізму - АЕЕ, серед правильних модусів першої фігури такого модусу немає. Але більший засновок - виділяюче судження, тому вивід є необхідним і істинним.
Розглянуті нами приклади показують, що силогізм, до складу засновків якого входить виділяюче судження, підлягає не всім, а лише деяким правилам. Це зумовлюється особливістю виділяючих суджень, розподіленістю їх термінів. Це слід враховувати при аналізі структури категоричного силогізму. Виявити видділяюче судження серед засновків силогізму допомагають колові схеми Ейлера.
Література для поглибленого вивчення розділу
A. Основна
1. Гетманова А.Д. Логика. - М.: Новая школа, 1995. - С. 126-136.
2. Жеребкін В.Є. Логіка. - X.: Основа; К.: Знання, 1999. - С. 108-134.
3. Кириллов В.И., Старченко A.A. Логика. - М.: Высшая школа, 1995. -С. 120-143.
4. Конверський А.Є. Логіка. - К.: Четверта хвиля, 1998. — С. 228-239.
5. Иванов Е.А. Логика. - М.: Издательство БЕК, 1996. - С. 173-200.
6. Свинцов В.И. Логика. - М.: Скорина; Весь мир, 1998. - С. 203-23 і.
7. Тофтул М.Г. Логіка: Навч. посібн. для студентів вищих навчальних закладів. - К.: Академія, 2003. - С. 170-184.
8. Хоменко І.В. Логіка: Підручник для студентів вищих навчальних закладів. - К.: Абрис, 2004. - С. 143-148.
B. Додаткова
1. Ивин A.A. Искусство правильно мыслить. - М.: Просвещение, 1990. - С. 6-57.
2. Кондаков Н.И. Логический словарь-справочник. - М.: Наука, 1975.
— Статті: аксиома простого категорического силлогизма, выведение, дедукция, модусы силлогизма, ошибки в неправильном силлогизме, правила простого категорического силлогизма, силлогизм, умозаключение, фигура силлогизма, энтимема, эпихейрема та інші статті до даної теми.
3. Логические методы и формы научного познания. - К.: Наукова думка, 1984.-200 с.
4. Мельников В.Н. Логические задачи. - К.; Одесса: Вища школа, 1989. -С. 292-314.
5. Шейко О.М. Скорочений силогізм. - К.: Вища школа, 1962. - 28 с.
Короткий зміст розділу
1. Поняття про виводи логіки висловлювань
2. Умовно-категоричні виводи
3. Розділово-категоричні виводи
4. Умовно-розділові виводи
5. Скорочені силогізми
Розділ 10. Індуктивний умовивід
Короткий зміст розділу
1. Загальна характеристика індуктивного виводу