Короткий зміст розділу
Умовиводи здійснюються не тільки з простих, але й зі складних суджень. Доволі широко використовуються виводи, засновками яких є умовні та розділові (диз'юнктивні) висловлювання. Такі висловлювання поєднуються в різних комбінаціях одне з одним або з категоричними судженнями. У залежності від цього існують різні види виводів логіки висловлювань.
1. Поняття про виводи логіки висловлювань
* Виводи логіки висловлювань г дедуктивними опосередкованими виводами. їх основна особливість полягає в тому, то тут враховується тільки структура складних висловлювань (молекул) і не враховується структура висловлювань, які є елементарними (атоми). Інакше кажучи, у виводах логіки висловлювань міркування будується винятково на логічних зв'язках між висловлюваннями.
Логічна схема (структура) виводу буде такою:
Аі, Аг, Ап або А,, А2, Ап Ь В.
В
У цій структурі висловлювання "А,, А,,..., Ап" є засновками, "В"- висновок.
Якщо кон'юнкція засновків, з'єднана з висновком знаком імплікації, є завжди істинною формулою (тавтологією), то такий вивід називають правильним:
(А, Л А, Л ... Л А ) —"В - завжди істинна формула.
Якщо ж знайдеться такий набір значень істинності засновків та висновку, при якому формула набуде значення істинності "хиба", то такий вивід називають неправильним.
Отже, правильний вивід відрізняється від неправильного тим, що в ньому між кон'юнкцією засновків та висновком існує відношення логічного слідування.
З наведених характеристик виводу логіки висловлювань витікає процедура перевірки його правильності. Для цього достатньо:
1. Формалізувати всі засновки та висновок.
2. Скласти кон'юнкцію формалізованих засновків і з'єднати їх з висновком знаком імплікації.
3. Побудувати таблицю істинності отриманої формули. Якщо формула є завжди істинною, то вивід правильний, якщо ні, то вивід неправильний.
2. Умовно-категоричні виводи
а) Суто умовні.
Суто умовним називають вивід, в якому всі засновки і висновок є умовними висловлюваннями. Наприклад:
Якщо успішно складу зимову сесію (А), то поїду в Карпати (В). Якщо поїду в Карпати (В), то обов'язково побуваю на Говерлі (С). Якщо успішно складу зимову сесію (А), то обов'язково побуваю на Говерлі (С).
Структура цього виводу є такою: Якщо А, то В. Якщо В. то С. Якщо А, то С.
Формула логіки висловлювань: ((А -" В) А (В -4 С)) —> (А —> С).
Ця формула є завжди істинною або законом логіки, оскільки структура цього виводу є правильною.
Вивід в суто умовному умовиводі грунтується на правилі: наслідок наслідку є наслідком підстави.
У суто умовному виводі існують його різновиди (модуси). До них належить, наприклад, такий:
Якщо А, то В.
Якщо не А. то В.
В.
Його формула: ((А -> В) Л (~А -> В)) -" В. Ця формула є законом логіки (тавтологією). Наприклад:
Якщо складу залік з логіки, то піду в кіно. Якщо не складу залік з логіки, то піду в кіно. Піду в кіно.
б) Стверджувальний модус
Умовно-категоричний умовивід - це вивід, в якому один Ь засновків - умовне судження, а інший - категоричне судження. Наприклад:
Якщо фотоплівку засвітити (А), то вона вийде з ладу (В). Цю фотоплівку засвічено (А).
Ця фотоплівка вийшла з ладу (В). Структура цього виводу: Якщо А, то В.
А._
В.
Його формула:
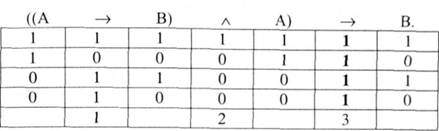
Як бачимо, формула логіки висловлювань, що відображає дану структуру виводу, є завжди істинною або законом логіки. Цю структуру виводу називають стверджувальним модусом (modus ponens) умовно-категоричного умовиводу, оскільки в ній від ствердження підстави (А) переходять до ствердження наслідку (В). Можна будувати достовірні умовиводи від ствердження підстави до ствердження наслідку. При цьому засновки повинні бути істинними.
Побудуємо тепер наше міркування так:
Якщо фотоплівку засвітити (А), то вона вийде з ладу (В).
Ця фотоплівка вийшла з ладу (В).
Цю фотоплівку було засвічено (А).
Його структура:
Якщо А, то В.
В._
А.
Формула логіки висловлювань:

Як бачимо, ця формула не є тавтологією. Отже, ми маємо справу з неправильною структурою виводу. Це означає, що вивід за цією структурою не є необхідним, тобто він не завжди буде давати істинні висновки. Не можна будувати достовірні умовиводи від ствердження наслідку до ствердження підстави. Цей модус умовно-категоричного умовиводу називають імовірним. Він не є законом логіки.
с) Заперечний модус.
Побудуємо наше розмірковування таким чином:
Якщо фотоплівку засвітити (А), то вона вийде з ладу (В).
Ця фотоплівка не вийшла з ладу (~В).
Цю фотоплівку не було засвічено (^А).
Структура цього міркування є такою:
Якщо А, то В.
Не В._
Не А.
Йому відповідає формула логіки висловлювань: ((А —" В) Л~В) —> ~А. Ця формула є законом логіки або завжди істинною формулою. Цей різновид умовно-категоричного умовиводу називають заперечним модусом (modus tollem). Він встановлює, що можна будувати достовірні умовиводи від заперечення наслідку до заперечення підстави. Не слід забувати, що засновки при цьому повинні бути істинними.
Наше міркування, нарешті, можна побудувати і таким чином:
Якщо фотоплівку засвітити (А), то вона вийде з ладу (В).
Цю фотоплівку не засвічено (~А).
Ця фотоплівка не вийшла з ладу (~В).
Структура цього умовиводу є такою:
Якщо А, то В.
Не А._
Не В.
Цій структурі відповідає наступна формула логіки висловлювань: ((А —> В) Л-А) —" ~В. Виходячи із міркувань здорового глузду, якщо фотоплівка не засвічена, це не завжди означає її придатність для використання. Тобто ця структура не завжди дає необхідні виводи, бо вона є неправильною. А формула, яка їй відповідає, не є законом логіки. Не можна будувати достовірні умовиводи від заперечення підстави до заперечення наслідку. Цей модус умовно-категоричного умовиводу називають імовірним.
1. Поняття про виводи логіки висловлювань
2. Умовно-категоричні виводи
3. Розділово-категоричні виводи
4. Умовно-розділові виводи
5. Скорочені силогізми
Розділ 10. Індуктивний умовивід
Короткий зміст розділу
1. Загальна характеристика індуктивного виводу
2. Повна індукція