Поняття про еластичність попиту
Форма кривої попиту та її нахил мають надзвичайно важливе значення в ціноутворенні, адже вони водобража-ють особливості реакцї покупців у відповідь на зміну ціни. Кількісно вимірити чутливість попиту до зміни ціни (або інших чинників) дає змогу еластичність. У математиці еластичність - це відношення темпів зростання залежної змінної до темпів зростання незалежної змінної. Коефіцієнт еластичності показує, на скільки відсотків зміниться залежна змінна при зміні незалежної змінної на 1%:

В економічному аналізі в якості залежної змінної найчастіше використовують такі величини як попит, виторг від продаж, прибуток та ін., а незалежної змінної - ціна товару, ціни взаємозв'язаних товарів, доходи споживачів, витрати на рекламу тощо.
Зважаючи на знак коефіцієнта еластичності (плюс або мінус), між змінними величинами спостерігається два типи залежності:
1) пряма (Е > 0) - зростання однієї змінної викликає зростання іншої;
2) зворотна (Е < 0) - зростання однієї змінної викликає зниження іншої.
Щодо еластичності попиту, то в економічній теорії і практиці розрізняють такі види коефіцієнтів еластичності попиту:
1) пряма еластичність попиту за ціною (цінова еластичність);
2) перехресна еластичність попиту за ціною;
3) еластичність попиту за доходом.
Кожен з цих видів еластичності можна розрахувати двома методами - точкової еластичності або дугової еластичності.
Цінова еластичність (еластичність попиту за ціною)
показує, на скільки відсотків зміниться величина попиту при зміні
ціни на 1%. Як було зазначено вище, для її визначення застосовують методи точкової чи дугової еластичності.
Метод точкової еластичності
Метод точкової еластичності передбачає розрахунок еластичності в конкретній точці (за конкретної ціни) й означає, що вимірюється попит при нескінченно малій зміні ціни (у практиці менше 5%). Можливі два варіанти розрахунку.
Варіант 1. Якщо відома функція попиту ОДР) і конкретна ринкова ціна Р, для якої потрібно розрахувати еластичність, то слід використовувати формулу:

Варіант 2. Якщо відомі початкові або кінцеві значення О і Р, причому зміна ціни не перевищує 5%, то використовується формула:

Слід зазначити, що за цим варіантом, зважаючи на незначний розрив між О1 і О2 та між Р1 і Р2, не має принципового значення, які з них обрати як початкові, а які - кінцеві, оскільки результати разюче не відрізнятимуться.
Геометричний сенс точкової еластичності полягає в тому, що вона характеризує кут нахилу кривої попиту в конкретній точці, хоч і не віддзеркалює загального характеру кривої попиту. Останнє вважається істотною вадою методу точкової еластичності.
Метод дугової еластичності
Метод дугової еластичності використовується за відсутності функції попиту і визначає еластичність, якщо відомі початкові і наступні значення О і Р, причому зміни між ними можуть бути досить значними (понад 5%). З метою усунення проблеми, які саме значення О і Р приймати початковими (попередні О1 і Р1 чи наступні О2 і Р2, оскільки це істотно впливає на результат), зазвичай обчислюють їх середню арифметичну, тоді цінова еластичність набуває вигляду:
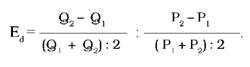
Графічно дугова еластичність ілюструється як еластичність в середині хорди (точка М на рис. 3.9), яка сполучає дві точки. Інакше кажучи, використовуються середні для дуги АВ значення ціни й обсягу попиту.
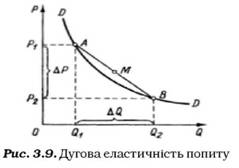
Дугова еластичність, вочевидь, дає змогу визначити лише приблизне значення еластичності на дузі АВ кривої попиту. Помилка буде тим більше, чим більш увігнутою до початку координат виявиться дуга АВ. Тим не менше до розрахунку еластичності дуговим методом дослідники вдаються набагато частіше, оскільки точно визначити функцію попиту вкрай проблематично.
Величина Еа може суттєво розрізнятися залежно від типу функції попиту і змінюватися від 0 до оо. Розглянемо варіанти можливих значень коефіцієнта еластичності.
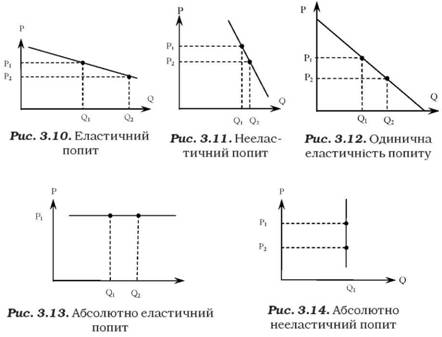
Варіант 1. Якщо |Еа | > 1, то попит є еластичним, тобто 1%а зміна ціни призводить до більшої відсоткової зміни величини попиту. Це означає, що попит росте швидшими темпами, ніж знижується ціна. На рис. 3.10 видно, що крива попиту є більш пологою.
Варіант 2. Якщо |Еа | < 1, то попит нееластичний, тобто 1%-а зміна ціни спричинює менш ніж 1%у зміну величини попиту. Це означає, що попит зростає повільнішими темпами, ніж знижується ціна. Крива попиту є крутішою (рис. 3.11).
Варіант 3. Якщо |Еа| = 1, то маємо одиничну еластичність попиту, за якої 1%-а зміна ціни призводить точно до 1%-ї зміни величини попиту. Інакше кажучи, темпи зміни попиту й ціни однакові. Крива попиту перетинає осі під кутом 45 0 (рис. 3.12).
Варіант 4. Якщо |Еа | -—оо , то попит абсолютно еластичний, тобто яка-небудь завгодно мала зміна ціни породжує значну зміну попиту на необмежено велику величину. Це означає, що навіть незначуще підвищення ціни призводить до того, що обсяг попиту тяжіє до нуля, а таке саме її зниження - до його необмеженого зростання. Крива попиту є майже паралельною осі абсцис (рис. 3.13). Вважається, що попит є абсолютно еластичним на ринку досконалої конкуренції. Проте слід наголосити, що оскільки грошові ресурси людей обмежені, то попит може бути абсолютний еластичним тільки в деякому діапазоні обсягу попиту, а також з великою часткою умовності.
Варіант 5. Якщо |Еа| = 0, то попит абсолютно нееластичний, тобто покупці не реагують на будь-яку зміну ціни й продовжують купувати продукцію в попередній кількості. Такий попит властивий ринку товарів першої потреби, як-от: хліб, цукор, сіль, ліки, сірники тощо. Гасло споживача в таких умовах: "Я повинен мати цей продукт, хоч би якою була його ціна". Графік попиту виглядає як пряма, паралельна осі ординат (рис. 3.14). Проте тут також слід згадати обмеженість грошових ресурсів споживачів, з чого випливає, що завжди існує таке підвищення ціни, яке зменшить попит на товар. Водночас еластичність одного конкретного покупця відносно конкретного товару цілком може виявитися нульовою для достатньо широкого діапазону цін.
Інтерпретація коефіцієнта цінової еластичності
Додамо також те, що внаслідок обмеженості доходів горизонтальна і вертикальна прямі попиту вважаються абстракціями, хоча в певних умовах попит на деякі товари може набувати близьких характеристик.
Розглядаючи різні варіанти еластичності попиту, ми аналізували значення коефіцієнта еластичності за модулем, тобто не беручи до уваги його знак. Це пояснюється тим, що в більшості випадків згідно з законом попиту Еа < 0 (чим більше ціна, тим менше попит). Але існують і виключення, коли за певних умов Еа може набувати позитивного значення. Це означає, що при підвищенні ціни товару всупереч всім законам логіки попит на нього зростає. Відомі дві такі ситуації:
1) "парадокс Гіффена" - при підвищенні цін на товари життєвого значення (хліб, картопля) люди з невисокими доходами збільшують на них попит, побоюючись ще більшого здороження;
2) "ефект Веблена" - при підвищенні цін на предмети розкоші (коштовності, ексклюзивний одяг, автомобілі) деякі люди, схильні до демонстративного споживання, купують їх у більших кількостях.
Приклад 3.2
Супермаркет "Афінна" реалізує гуртом та уроздріб широке різноманіття харчової і промислової продукції. Упродовж звітного кварталу отримано функцію попиту на картоплю у вигляді 06 = 400 - 2Р, де Р - ціна 1 кг, яка трималася на рівні 2 грн/кг. Також були проведені цінові експерименти щодо однієї з марок дорогого коньяку та емульсійної фарби: ціна на коньяк була знижена з 400 до 385 грн за пляшку, що збільшило обсяг продажу впродовж трьох днів з 40 до 45 пляшок; а здешевлення фарби для гуртових покупців з 24 до 18 грн за банку за два тижні призвело до зростання збуту з 10 000 до 18 000 банок.
Для визначення цінової еластичності кожного товару потрібно застосовувати різні методи.
Для картоплі слід застосувати 1-й варіант методу точкової еластичності, тому що точно відома ринкова ціна товару та функція його попиту:
Р 2 2
Б, =0'(Р)----= - 2 •-----------= - 2 •-----= - 0,010%.
О(Р) 400 - 2 • 2 396
Оскільки за модулем коефіцієнт еластичності менше одиниці, то попит на картоплю нееластичний, відтак 1%-е зростання цін на цей продукт відносно початкового рівня (2 грн/кг) призведе до зниження попиту на 0,010%. Таким чином, знижувати ціну не треба.
Для коньяку доцільно використати 2-й варіант методу точкової еластичності, адже зміна ціни перебуває в межах 5%, що гарантує відносно надійний результат:
02 - 01 Р2 - Р1 45 - 40 385 - 400
Б, =------ : --2---- =-------:--------= 0,125 : (-0,038) = - 3,29%.
6 01 Р1 40 400
Попит на коньяк еластичний, оскільки | - 3,29% | > 1. Ціну коньяку можна знижувати, і це спричинить значне зростання обсягу збуту. Для емульсійної фарби треба скористатися формулою дугової еластичності, позаяк зміна ціни значно перевищує 5% і становить (24 - 18) : 24 • 100 = 25%. Коефіцієнт еластичності є таким:
<32 - <з Р2 - Р1 18 000 - 10 000 18 - 24 8000 - 6
6 (<32 + 01) : 2 ' ( Р2 + Р1) : 2 (18 000 + 10 000) : 2 ' (18 + 24) : 2 14 000 ' 21
Оскільки - 2% > 1, попит еластичний, тож при зниженні ціни на 1% обсяг продаж зростає на 2%. Ціну можна знижувати.
Інтерпретація коефіцієнта цінової еластичності
3.3. ЗАСТОСУВАННЯ ЦІНОВОЇ ЕЛАСТИЧНОСТІ ПОПИТУ В ЦІНОУТВОРЕННІ
3.4. ПЕРЕХРЕСНА ЕЛАСТИЧНІСТЬ ПОПИТУ
3.5. ЕЛАСТИЧНІСТЬ ПОПИТУ ЗА ДОХОДОМ
3.6. ПРОГНОЗУВАННЯ ЗМІНИ ПОПИТУ ПРИ ЗМІНІ ЦІНИ
3.7. ПРАКТИЧНІ СПОСОБИ ВИЗНАЧЕННЯ ПОПИТУ І ЙОГО ЦІНОВОЇ ЕЛАСТИЧНОСТІ
Дослідження даних про продаж
Вивчення панельних даних
Дослідження магазинів