Ринкове ціноутворення - Мазур О.Є. - 4.6. ЦІНОУТВОРЕННЯ В УМОВАХ РИЗИКУ І НЕВИЗНАЧЕНОСТІ

Ухвалення цінових рішень зазвичай потребує вибору між різними стратегіями і ускладнене тим, що особа, яка приймає рішення, має передбачити майбутні події, котрі можуть вплинути на очікуваний результат. Ці події стосуються змін у внутрішньофірмових умовах діяльності, попиті, погодних умовах, політичній кон'юнктурі та ін. Деякі з них менеджери здатні контролювати, деякі взагалі не підлягають контролю і навіть прогнозуванню. Отже, стани особи, яка приймає рішення стосовно майбутньої ціни товару, класифікують як стани визначеності, ризику й невизначеності. Відмінності між ними відображують різну міру знань менеджерів. Якщо уявити ці знання як лінію спектру, то на одному її кінці буде визначеність (повне знання), на іншому - невизначеність (повна відсутність знання), а між ними розташується ризик (часткове знання). Поточне розташування менеджера на лінії буде віддзеркалювати рівень визначеності у прийнятті цінового рішення.

Концепція визначеності - це такий стан знання, за якого менеджер заздалегідь має вичерпну інформацію про стан середовища, а відтак знає конкретний результат для кожної альтернативи.

На перший погляд здається, ніби така концепція є нереалістичною, проте існує чимало практичних ситуацій короткострокового характеру, коли менеджери володіють вичерпною інформацією. Проте це не є справедливим для довгострокового терміну, адже передбачити значну кількість динамічних взаємовпливів невідомих змінних, які нас цікавлять, можливо лише у виключних випадках.

Концепція ризику передбачає інформованість про один чи кілька результатів кожної альтернативи, а також ймовірність їхнього настання. Інакше кажучи, менеджер має певне об'єктивне знання про середовище та здатен об'єктивно прогнозувати ймовірну сутність явищ та результат чи віддачу по кожній з можливих стратегій. Концепція невизначеності - це стан, за якого одна чи кілька альтернатив мають ряд можливих результатів, ймовірність яких невідома. Зазвичай такий стан має місце, якщо не існує надійних даних, на базі яких можна було б розрахувати ймовірності. Тому на відміну від ризику прийняття рішень в умовах невизначеність завжди є суб'єктивним: два спостерігачі, які розглядають певну ситуацію, ніколи не дадуть однаковий прогноз - надто не передбачуваними є майбутні зміни.

Розроблення цінового рішення в умовах визначеності здійснюють за допомогою широкого кола методів встановлення ціни, які ми розглядали, - з орієнтацією на витрати, попит, конкуренцію та параметричних. Ціноутворення в умовах ризику й невизначеності ґрунтується на різних економіко-математичних підходах, але кожен з них допомагає своєчасно вибрати оптимальний альтернативний варіант ціни, який дає змогу послабити чи уникнути впливу ризику на фінансові результати. Розгля-немо їх докладніше.

Найчастіше аналіз цінових рішень здійснюють за допомогою теорії ігор, яка досліджує оптимальні стратегії в ситуаціях ігрового характеру, де перетинаються інтереси двох чи більше конкуруючих сторін, які мають різні цілі. Термінологія теорії ігор запозичена зі спортивних і азартних ігор: її учасники називаються гравцями, а оцінка результату гри - виграшем (програшем). В ролі гравців можуть виступати окремі особи, колективи людей або цілі організації (підприємства), що переслідують свої цілі. Якщо в грі стикаються інтереси двох гравців, то вона називається парною грою, а якщо більше - множинною грою.

Залежно від характеру виграшу розрізняють три типи ігор: з позитивною, негативною і нульовою сумою виграшу.

Гра з позитивною сумою виграшу - гра, в якій сам процес змагання приносить користь всім його учасникам. Інакше кажучи, така гра вигідна не лише переможцеві, а й тому, хто програв, оскільки в будь-якому разі і він отримає щось позитивне для себе. Така модель лежить в основі спортивної і наукової діяльності. Тому чим довше продовжується така гра, тим більше виграш для гравців.

Гра з нульовою сумою виграшу - змагання, в якому сума виграшів всіх учасників дорівнює нулю. Простіше кажучи, один гравець виграє рівно стільки, скільки програє інший.

Гра з негативною сумою виграшу - вид змагальної діяльності, в якій всі учасники змушені нести витрати, але навіть переможець може отримати виграш менший, ніж його витрати. Така гра гарантує витрати, але не гарантує обов'язкового отримання вигоди - наприклад, війни, дуелі, трудові конфлікти та ін. Той, що програв, ніколи не отримає для себе жодного виграшу. Більш того, чим довше триває така гра, тим ймовірніше, що навіть переможець врешті-решт вирішить для себе, що розпочинати гру було не варто.

Цікаво, що ціноутворення в багатьох випадках є грою з негативною сумою виграшу, особливо це проявляється в сфері цінової конкуренції компаній. Насправді, чим довше триває цінова конкуренція і чим запекліший характер вона має, тим сильніше підривається цінність для конкуруючих фірм того ринку, за який вони борються. Цінова конкуренція може перетворитися на гру з позитивною сумою виграшу лише за виняткових обставин:

• якщо попит на даний товар високоеластичний, і зниження цін породжує різке його збільшення;

• якщо збільшення попиту веде до такого зростання продажу, що відповідне йому зростання виробництва породжує ефект масштабу, достатній для компенсації початкового падіння прибутковості через зниження ціни.

От чому цінової конкуренції краще уникати. Перш ніж вплутатися в цінову боротьбу, варто подивитися на неї з позицій гравця, який приречений зазнати втрат навіть у разі перемоги. У цьому сенсі для менеджерів і фахівців з ціноутворення корисною є логіка компромісу і здатність "перемагати у війнах, не вступаючи в них".

Водночас найбільш простою і теоретично розробленою грою є гра двох осіб з нульовою сумою, яка і буде об'єктом нашого вивчення при ухваленні рішення про ціну.

Рішення задач такого типу потребує визначення кількості гравців, правил гри, можливих стратегій поведінки гравців і можливих виграшів гравців (негативний виграш розуміють як програш).

В задачах про ціноутворення в якості гравців найчастіше виділяють фірму, яка встановлює ціну, і споживачів, які реагують на неї своїм попитом. Стратегії, тобто дії гравців, можуть бути кінцевими і нескінченними. При дослідженні кінцевої гри складають матриці виграшів, а нескінченної - функції виграшів. При цьому як виграш використовують прибуток (збитки) підприємства від встановлення тієї чи іншої ціни. Таким чином, менеджер розглядає всі можливі ціни, очікуваний від них прибуток і обирає найбільш прийнятну ціну.

Для ухвалення цінового рішення менеджер розглядає всі альтернативи і стани природи. Альтернатива - напрям дії або стратегія, яку може вибрати той, хто ухвалює рішення (можлива ціна). Стан природи - ситуація, на яку менеджер не може вплинути або його вплив обмежений (обсяг попиту, погодні умови та ін.). Зрештою вибирається та альтернатива, яка у поєднанні зі станом природи дасть оптимальний грошовий результат.

Якщо це ситуація ризику, то найбільш загальним критерієм вибору альтернативи є величина очікуваної цінності (вартості) того чи іншого варіанту. Якщо ситуація невизначеності - то процедура рішення ухвалюється на основі інших критеріїв.

Методика аналізу в будь-якому разі включає побудову платіжної матриці (платіжної таблиці, таблиці рішень). Платіжна матриця - таблиця, в лівій частині якої записують всі альтернативи (ціни), у верхній частині - стани природи (попит, погода, доходи та ін.), а в центрі розміщують значення очікуваного грошового результату (прибутку), відповідного кожному поєднанню альтернативи і природи.

Розглянемо в якості прикладу умовне підприємство, яке є виробником авторучок, що їх воно реалізує гуртом місцевому невеликому універмагу. Змінні витрати на одну авторучку становлять 5 грн, місячні постійні витрати - 1500 грн. Менеджери розглядають три варіанти роздрібної ціни - 6, 8 і 10 грн. Дослідження показали, що попит на ручки в регіоні може коливатися в межах 1000 - 1600 од. щомісяця. Менеджерам невідомі ймовірності появи того чи іншого рівня попиту, а відтак ми маємо справу з станом невизначеності.

Залежно від можливих змін попиту, які визначені суб'єктивно (на основі експертних оцінок), розраховані варіанти прибутку, які представлені у вигляді платіжної матриці (табл. 4.32).

Таблиця 4.32. Платіжна матриця для підприємства "Агрус"

Якби ми розглядали ситуацію в стані визначеності, то оперували б тільки одним-єдиним станом попиту, а платіжна матриця була б зведена до одного стовпця. В таких умовах менеджер точно знав би, що віддача з'явиться лише тоді, якщо буде впроваджена конкретна стратегія, і йому достатньо було тільки обрати стратегію з найбільшою віддачею.

У випадках, коли менеджери можуть визначити ймовірність досягнення тієї чи іншої величини попиту, тобто при аналізі ризику, зручно користуватися замість платіжної матриці методом дерева рішень. Дерево рішень - це графічне зображення процесу, де визначені альтернативи рішень, стани природи і відповідна ним ймовірність грошової віддачі для кожної комбінації альтернатив і станів природи. Зазвичай використовують такі позначення:

□- вузол рішення, з якого можна вибрати одну чи кілька альтернатив;

О - вузол стану природи, з якого може з'явитися один стан природи.

Якщо в завданні є один тип альтернативи і один тип стану природи, то зручніше користуватися платіжною матрицею, а якщо існує два чи більше послідовних рішень, причому подальші рішення базуються на попередніх, то варто будувати дерево рішень.

Далі для кожного варіанту обчислюють показник очікуваної грошової віддачі (Expected Monetary Value - EMV) - суму можливих значень віддачі (прибутку), зважених на ймовірність їх досягнення. Цей показник являє собою очікувану цінність певного варіанту і обчислюється так:

EMV = EAR ,

де А_і - значення прибутку для і-го стану природи; Р_і - ймовірність настання і-го стану природи.

З цієї формули очевидно, що прогнозована вартість призначення тієї чи іншої ціни являє собою середньозважену вартість, в якій у якості вагових коефіцієнтів використовують ймовірності віддачі. Таким чином, можна стверджувати, що якби стратегію ціни застосовували б багато разів при аналогічних варіантах, то можна було б розраховувати на отримання середньої віддачі, яка і дорівнює величині ЕМУ.

Критерієм вибору альтернативної ціни виступає максимальне значення ЕМУ.

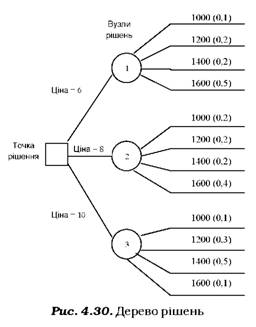
Продовжимо приклад. Припустімо, менеджери не можуть точно визначити, яким буде майбутній попит на авторучки при кожній можливій ціні, проте можуть приблизно визначити ймовірність його досягнення. Проведемо аналіз за допомогою дерева рішень (рис. 4.30), на якому позначені варіанти обсягів продажу за кожної ціни та в дужках ймовірність їхнього досягнення.

Розрахуємо очікувану грошову віддачу (ЕМУ) для кожного вузла: ЕМУ(1) = -500 • 0,1 - 300 • 0,2 - 100 • 0,2 + 100 • 0,5 = = -50 - 60 - 20 + 50 = -80 грн ЕМУ(2) = 1500 • 0,2 + 2100 • 0,2 + 2700 • 0,2 + 3300 • 0,4 =

= 300 + 420 + 540 + 1320 = 2580 грн

ЕМУ(3) = 3500 • 0,1 + 4500 • 0,3 + 5500 • 0,5 + 6500 • 0,1 =

= 350 + 1350 + 2750 + 650 = 5100 грн

Найбільший прибуток обіцяє варіант 3, який передбачає встановлення ціни 10 грн.

Якби підприємство перебувало в стані невизначеності, і ймовірності попиту залежно від ціни були б невідомі, то при ухваленні рішення про ціну менеджерам варто було б орієнтуватися на мак-симінні стратегії, а також критерії Гурвіця й Севіджа.

Проведемо аналіз максимінних стратегій (табл. 4.33).

Таблиця 4.33. Застосування максимінних стратегій

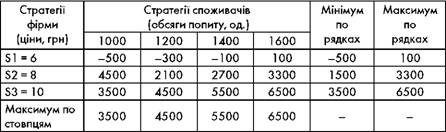
Підприємство може вибрати чотири стратегії:

1) Максимізація максимальних результатів - найбільш оптимістичний прогноз, який обіцяє найкращий результат. Для цього знаходимо максимальні значення прибутку по рядках, з яких ясно, що найбільший прибуток 6500 грн досягається при виборі стратегії Б3 - призначенні ціни 10 грн:

шах (100, 3300, 6500) = 6500 грн. Вибір стратегії, яка обіцяє надмірно оптимістичні результати, є недоцільним, адже прогноз може не здійснитися, і фірма зазнає збитків.

2) Максимізація мінімальних результатів (стратегія максиміна, або критерій Вальда) - вибір песимістичної

стратегії, яка обіцяє кращий з усіх найгірших результатів по кожній стратегії. Для цього розраховуємо мінімальні значення прибутку по рядках і вибираємо з них максимальне: шах (-500, 1500, 3500) = 3500 грн. Цей прибуток відповідає стратегії Б3 (ціна 10 грн). Можна бути упевненим, що призначивши таку ціну, при будь-якій з умов кон'юнктури ринку чистий результат буде не гірший, ніж 3500 грн. Тому таку стратегію називають нижньою ціною гри, або максиміном. Максимінна стратегія є єдиною абсолютно надійною при ухваленні рішень в умовах невизначеності.

3) Мінімізація максимальних результатів (стратегія мінімакса) показує найгірший ре-зультат з усіх найкращих. Для цього по рядках підраховуємо максимальний прибуток і вибираємо з цих значень найменше:

шіп(100, 3300, 6500) = 100 грн. Ця величина називається верхньою ціною гри, або мінімак-сом. Її використання забезпечує гарантований мінімальний прибуток з усіх максимальних результатів дії кожної стратегії. В нашому прикладі це стратегія Б1 (ціна 6 грн).

4) Мінімізація мінімальних результатів - показує найменший виграш (найбільшу втрату) з усіх можливих. Вибираємо найменше значення з мінімальних по рядках значень:

шіп(-500, 1500, 3500) = -500 грн.

Якщо фірма прийме стратегію Б1 і призначить ціну 6 грн, то вона має бути готова до того, що якщо попит виявиться найсприятливішим (1000 од.), вона зазнає збитків в розмірі 500 грн.

Остаточний вибір ціни здійснюється менеджером, виходячи із завдань компанії, її схильності до ризику, поточних показників прибутковості та ін.

Ще один критерій - критерій Гурвіця - дає змогу вибрати оптимальне рішення між двома крайнощами: максимаксною і максимінною стратегією, тобто між песимістичною оцінкою і надмірним оптимізмом. Ваговими факторами слугують при цьому коефіцієнт (ступінь) оптимізму х, який застосовують до мак-симаксної віддачі, та його доповнення (1 - х), яке застосовують до максимінної віддачі. Тоді грошова віддача кожної стратегії дорівнює:

Є = х • Мах + (1 - х) • Міп, де Мах - значення максимуму по рядках, Міп - значення мінімуму по рядках.

Альтернатива (цінова стратегія) з найбільшою вартістю величини Є є оптимальною.

Значення коефіцієнту оптимізму перебуває в межах від 0 до 1, причому при х = 0, тобто при пе-симістичному настрої, отримуємо максимінну стратегію, а при х = 1, тобто налаштувавшись абсолютно оптимістично, - максимаксну. Отже, рішення, прийняте згідно з критерієм Гурвиця, залежить від величина х, яка, своєю чергою, обумовлена власним відношенням менеджера, який приймає рішення, до ризику.

Так, якщо в нашому прикладі менеджер дотримується оптимістичної оцінки попиту і вважає, що х = 0,7, тоді песимістична оцінка становитиме 1 - х = 1 - 0,7 = 0,3, а лінійні комбінації мінімального і максимального виграшів для кожної стратегії матимуть вигляд:

= 0,7 • 100 + 0,3 • (-500) = - 80 грн (значення 100 і -500 вибираємо по рядках як мінімальні і максимальні) = 0,7 • 3300 + 0,3 • 1500 = 2760 грн. = 0,7 • 6500 + 0,3 • 3500 = 5600 грн.

Є = шах (-80, 2760, 5600) = 5600 грн.

Таким чином, за критерієм Гурвіця найбільш раціональний варіант ціни - 10 грн (стратегія Б1).

Математична теорія ігор також пропонує скористатися критерієм мінімальних втрат (мінімізації ризику) - критерієм Се-віджа. Згідно з цим критерієм, потрібно обрати таку стратегію, за якої вели-чина втрат набуває мінімального значення в найсприятливішій ситуації. Критерій Севіджа досліджує збитки, які являють собою втрати, що їх може зазнати підприємство від неправильно прийнятого цінового рішення. Втрату вимірюють як різницю між максимально можливим виграшем при заданому стані природи і виграшу від обраної стратегії за того самого стану природи.

Логіка розрахунку проста: якщо ми обрали стратегію, яка забезпечує максимальну віддачу для певного стану природи в майбутньому, то ми не рахуємо збитки. Але якщо ми обираємо будь-яку іншу стратегію, то втрата являє собою різницю між тим, що відбувається фактично, і тим, що можна було б отримати, ухваливши більш оптимальне рішення.

Таблиця 4.34. Матриця ризиків підприємства

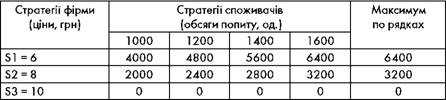
В нашому прикладі обчислимо максимальні значення прибутку по стовпцях і з них віднімемо значення прибутків, розташовані в центрі таблиці. В результаті отримаємо матрицю (табл. 4.34).

Наприклад, для стовпця, відповідного попиту 1000 од.:

3500 - (-500) = 4000

3500 - 1500 = 2000

3500 - 3500 = 0

За критерієм Севіджа мінімальні втрати забезпечує стратегія S3, оскільки значення ризику тут мінімальне: min r = min(6400, 3200, 0) = 0