Статистичні показники, що розкривають властивості вибірки, можна представити такими основними групами:
- емпіричними розподілами (варіаційними, атрибутивними, ранжирова-ними), що характеризують структуру досліджуваної властивості;
- вибірковими показниками (мірами центральної тенденції і мінливості), які представляють чисельні значення типових властивостей вибірки;
- кореляційно-регресійними показниками (коефіцієнтами кореляції, регресії), які дають можливість встановити приховані взаємозв'язки та закономірності явищ, спрогнозувати розвиток досліджуваних процесів.
2.1. ЕМПІРИЧНІ РОЗПОДІЛИ
Варіаційні ряди та статистичні розподіли
Емпіричні дані, які отримані шляхом вимірювань властивостей вибіркових об'єктів, повинні пройти первинну обробку і систематизацію: внесення у табличні форми (етап табуляціі), упорядкування у варіаційні послідовності (ряди), представлення у вигляді емпіричних розподілів4.
Приклад 2.1. Систематизувати результати виконання випадковою вибіркою студентів тестових завдань: 3, 4, 4, 4, 3, 2, 4, 4, 5, 1 (обсяг вибірки п = 10) .
Послідовність рішення:
o припустимо, що результати виконання тестових завдань адекватно характеризують досліджувану властивість5 студентів, яку позначимо змінною X;
o за умовами прикладу зміннаXприймає значення: х1 = 3, х2 = 4, "., х10 = 1;
o первинні емпіричні дані (х,) внесено у перші два стовпчики табл. 2.1;
o упорядковані дані (х/ ) представлено як варіаційний ряд у третьому сто-
4 Емпіричні розподіли іноді мають і такі назви: "статистичні розподіли", "вибіркові ряди розподілу", "емпіричні розподіли частот", "розподіли емпіричних даних" та ін.
5 Наприклад, успішність розв'язування логічних завдань, рішення проблемних ситуацій, уміння виконувати різноманітні вправи тощо.
впчику табл. 2.1;
o значення варіант (х) та їхня кількість (ш,) наведено в останніх двох стовпчиках табл. 2.1.
Таблиця 2.1
Систематизація результатів виконання тестових завдань (x)
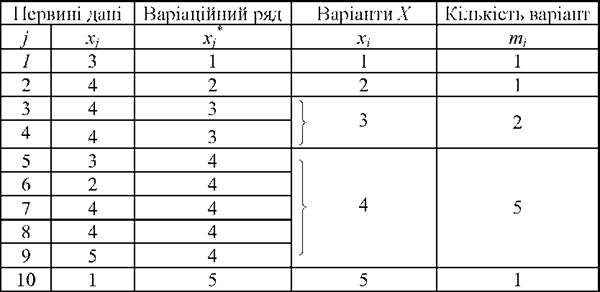
Як бачимо, варіаційний ряд - це упорядкована за збільшенням (або за зменшенням) послідовність значень досліджуваної змінної X (у табл. 2.1 значення х/). Варіаційний ряд дає можливість наочно і швидко сприйняти структуру даних: варіанти значень (х), які може приймати і приймає змінна X, а також кількість відповідних варіант (т), їхні мінімальне і максимальне значення. Варіаційний ряд дозволяє безпосередньо оцінити деякі важливі показники вибірки, наприклад, моду і медіану. Систематизація даних у варіаційний ряд є підготовчим етапом до розрахунків і побудови статистичних розподілів досліджуваної змінної.
Статистичний розподіл - це математична модель об'єктів реальності у вигляді співвідношення значень змінної X, що характеризує властивості вибірки, до частот їх появи. Наприклад, стовпчики значень хі (варіанти X) і значень ті (кількість варіант) у табл. 2.1 по суті утворюють статистичний розподіл, який розкриває залежність частоти появи (/і) від значень (хі) змінної, тобто / ~ хі. Отже, під поняттям "статистичний розподіл"/(х) слід розуміти емпіричний розподіли частот появи певних значень досліджуваної змінної (слово "частота" нерідко опускають, маючи на увазі його присутність). Частота / - це функція, де аргументом виступає варіанта х;.
Статистичні розподіли можна класифікувати за ознакою типів вимірювань6 змінної на: варіаційні, ранжировані та атрибутивні (рис. 2.1).
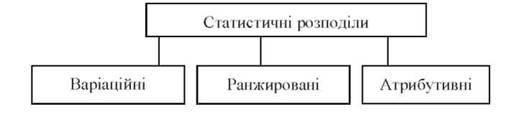
Рис. 2.1. Класифікація статистичних розподілів за типами вимірювань
Варіаційні розподіли базуються на даних, які виміряні за шкалою відношень або інтервалів. Ранжировані розподіли застосовуються у разі порядкових (рангових) типів вимірювання. Атрибутивні розподіли характеризують дані, які виміряні за номінальними шкалами або шкалами "найменувань".
Основні види статистичних розподілів такі: диференціальні та інтегральні, які можуть складатися з абсолютних і відносних частот (рис. 2.2).
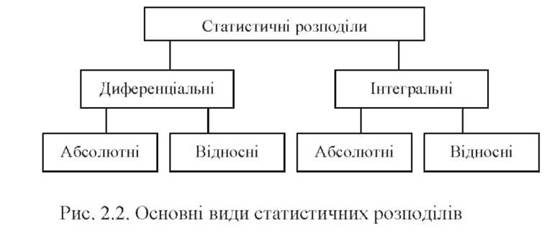
Диференціальні розподіли представляють значення частот окремо (тобто диференційовано) для кожної варіанти х,- змінної X.
Диференціальні абсолютні частоти - це кількості об'єктів мі з однаковими значенням хі змінної X(або кількість однакових значень).
Диференціальні відносні частоти - це відношення диференціальних абсо-
6 Найчастіше використовується класифікація Стівенса 4-х типів вимірювань: за шкалами відношень, інтервалів, порядковими та номінальними [59].
лютних частот ті до загальної кількості п об'єктів, тобто /і = ті/п.
Інтегральні розподіли ( "накопичені" або "кумулятивні") формуються як доданки попередніх диференціальних частот. Вони визначають сумарні частоти для варіанти, що не перевищує значення х,-змінної X.
і
Інтегральні абсолютні частоти У_| ті - це накопичена сума диференціальних абсолютних частот від 1-ї доу-ї варіанти.
і
Інтегральні відносні частоти Е] = ^ /і - це накопичена сума диференціальних відносних частот від 1-ї доу-ї варіанти.
Варіаційні розподіли у разі інтервальних або відносних типів вимірювань залежать від:
o характеру досліджуваної змінної - дискретна змінна, чи неперервна;
o діапазону значень змінної - вузький і невеликий, чи широкий і різноманітний.
Тому за технологією побудови варіаційні розподіли поділяють на розподіли незгрупованих і згрупованих варіант7. З метою лаконічності домовимося їх називати незгрупованими і згрупованими розподілами. Для незгрупованих розподілів частоти мають відношення до безпосередніх значень варіант з варіативного ряду; для згрупованих розподілів - до груп (або інтервалів) значень варіант.
Згруповані розподіли
Атрибутивні розподіли
Ранжировані розподіли
2.2. ПОКАЗНИКИ ВИБІРКИ
Міри центральної тенденції (МЦТ)
Міри мінливості (ММ)
Розрахунки та інтерпретація МЦТ і ММ
Початкові та центральні моменти
Квантилі