Математична статистика - Руденко В.М. - Характеристики випадкових величин

Випадкову величину X можна повноцінно характеризувати функцією розподілу подій сс>і, (функція визначена на просторі елементарних подій £2). Функція розподілу у вигляді гістограми (для дискретної змінної) або функції щільності (для неперервної змінної) дає вичерпну інформацію щодо закону розподілу випадкової величини. Проте спостерігаються завжди тільки значення цієї функції, які є реалізацією випадкової величини у конкретній ситуації. Сама ж функція розподілу є лише теоретичним узагальненням, яке служить основою для побудови імовірнісних моделей вивчення реальності.

Результати випробувань, як правило, моделюються незалежними випадковими величинами. Часто вважають, що спостереження, іспити, досліди проводяться за схемою незалежних іспитів. Отже, незалежність випадкових величин - одне з базових понять теорії ймовірностей, що лежить в основі практично всіх ймовірносно-статистичних методів. Тому слід мати на увазі деякі важливі властивості незалежних випадкових величин:

o випадкові величини X і У, визначені на тому ж самому просторі елементарних подій, називаються незалежними, якщо для будь-яких чисел а і Ь події {Х=а} і {У=Ь} є незалежними;

o якщо випадкові величини X і У незалежні, а і Ь - деякі числа, то випадкові величини Х+а і У+Ь також незалежні;

o якщо випадкові величини X і У незалежні, аЛ(Х) і g(У) - випадкові величини, отримані з X і У за допомогою деяких функцій/і g, то Л(Х і <?(У - ^також незалежні випадкові величини. Наприклад, якщо X і У незалежні, то X ² і 3-У +4 незалежні, а також ln(X ) і 1п(У) незалежні.

У практиці досліджування генеральної сукупності цілком достатнім є отримання декількох чисельних характеристик, що оцінюють центр групування значень випадкової величини, міру їхнього розсіяння, ступінь взаємозв'язку різних компонентів багатомірної ознаки. У свою чергу, знаючи лише характер статистичних законів, розподіл може бути успішно відновлено за своїми чисельними характеристиками, наприклад, за середніми значеннями, дисперсією. Тож доцільно розглянути основні характеристики випадкової величини X, що дають змогу чисельно оцінити так звані показники "центральної тенденції" (математичне сподіванняM[X], моду Mo[X] і медіану Md[X), а також "варіативності" (дисперсія D[X], стандартне відхилення 5D[X]) .

Математичне сподівання

Однією з важливих характеристик розподілу випадкової величини X є її математичне сподівання M[X] (іноді його називають середнє значення випадкової величини).

Означення. математичне сподівання випадкової величини є число

M [ X ] =Х X(a) o P(a), (3.21)

weq

де Х(ю) - значення випадкової величини X, отримане у події ю; Р(ю) -ймовірність випадкової події ю; Q - простір елементарних подій ює£1

Приклад 3.13. Обчислити математичне сподівання числа, що випадає на верхній грані ігрового кубика.

Рішення:

Простір Q складається з 6 елементарних подій (ю₁, ю₂, ю₆}. Кожній елементарній події відповідає значення випадкової величини. Для ігрового кубика це число від 1 до 6 на його гранях: X(ro₁) = 1, X(ro₂) = 2, ... X(co₆) = 6. Всі події мають рівні ймовірності відбутися Р(ю{) = Р(ю₂) =... Р(ю₆) = 1/6.

Звідси математичне сподівання випадкової величини дорівнюватиме:

M[ X ] = X X (ю) o P(o) = 1- - + 2 o - + 3 o - + 4 o - + 5 o - + 6 o - = ²¹ = 3,5.

oieQ 6 6 6 6 6 6 6

Відповідь: математичне сподіванняA/[X⁷]=3,5.

Математичне сподівання простої випадкової величини X з множиною значень {x₁, x₂, x_n} визначається як

M[X] = Іх,. o Р(Х = х,.). (3.22)

Сенс математичного сподівання варто розкрити на прикладі.

Приклад 3.14. Середня кількість виконаних тестових завдань, що припадає на одного студента, може певним чином характеризувати якість навчання. Це можна прийняти, якщо припустити, що окремі значення випадкової змінної x групуються біля цього середнього показника. У табл. рис. 3.20 наведено дані іспитів: хі - можлива кількість виконаних завдань з п'яти запропонованих; т-^ - відповідна кількість виконань = т). Необхідно розрахувати математичне сподівання як орієнтовний показник навчальних досягнень студентів або якості навчання. Рішення:

o У стовпчику О (рис. 3.20) для кожного значення хі розрахувати відносні частоти Лі = т/т, прийнявши їх за статистичні ймовірності Р; (x = х^. Таке припущення справедливе при великій кількості випробувань.

o У стовпчику Е (рис. 3. 20) розрахувати зважені значення хі Л

o Побудувати графік розподілу виконання тестових завдань (рис. 3.21 ).

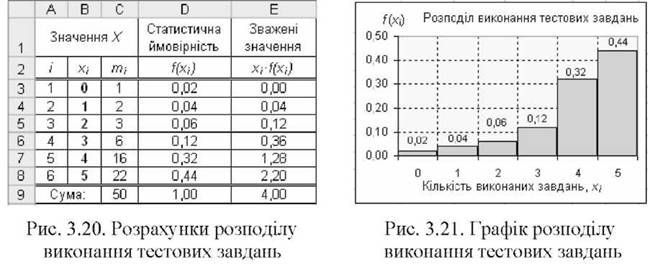
o Розрахувати математичне сподівання:

М[X] = £х,. o /(х,.) = 0o 0,02 +1-0,04+2o 0,06+3-0,12+4o 0,32+5o 0,44=4,00.

Відповідь: середнє значення кількості виконаних завдань, здобуте за результатами іспитів, близьке до математичного сподівання М[Х] = 4,00 і може служити орієнтовним показником якості навчання.

Для неперервної випадкової величини X, якщо функція розподілу р(х) абсолютно неперервна і невід'ємна, функція/(х) щільності розподілу така, що

р (х) =| / (х)оХ. (3.23)

-сс

Тоді математичним сподіванням називається число

+сс

М[ X ] = х ■ Л (х)сІх. (3.24)

-сс

Приклад 3.15. Розрахувати математичне сподівання неперервної випадкової величини X з рівномірнім розподілом імовірності на відрізку [а, Ь]. Рішення:

На рис. 3.22. зображено графік рівномірного розподілу X на відрізку [а, Ь].

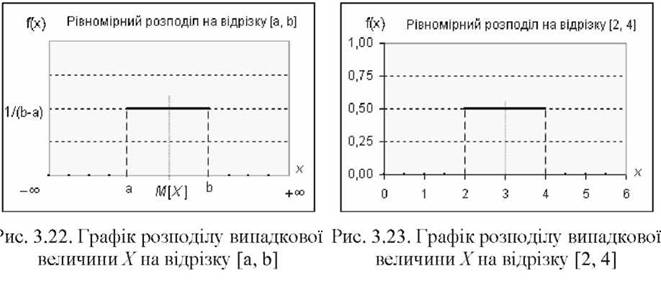
Математичне сподівання M[X] розраховується як визначний інтеграл на відрізку від -ж до +со, а саме

М[ X ] = | х o Л (х)Сх.

-сс

Щільність рівномірного розподілу Л(х) на відрізку [-о, +со] можна визначити на трьох окремих ділянках значень аргументу х:

Відповідь: у загальному вигляді математичне сподівання М[X] = ^Ь~2~~. Д^ля

конкретних значень відрізку [а, Ь], наприклад, а = 2 і Ь = 4, математичне споді -4 + 2

вання М [ X ] = -2- ⁼ 3. На рис. 3.23. зображено графік рівномірного розподілу

випадкової величини X на відрізку [2, 4] і відмічено положення MX = 3.

Емпіричним (тобто побудованим за вибірковими даними х₁, х₂, "., х_п) аналогом математичного сподівання є середнє арифметичне

_ 1 "

X = -1 х, . "1=1

Пояснення такого переходу від теоретичних характеристик до емпіричних (наприклад, від математичного сподівання M[X]) до середнього X ) базується на інтерпретації вибірки як зменшеної моделі генеральної сукупності, де можливими значеннями є вибіркові значення, а ймовірностями - відносні частоти їх появи у вибірці.

Розподіли випадкової величини X можуть бути охарактеризовані ще двома мірами положення центру: модою Mo[X] і медіаною Md[X].

Означення. Модою Mo[X] випадкової величини X називають таке її значення, при якому щільність ймовірності досягає максимуму¹³.

Для дискретної величини модою є найбільш імовірне значення випадкової величини. Наприклад, з рис. 3.21 можна встановити, що максимальну ймовірність 0,44 має значення 5. Отже, це значення і є модою Mo[X] = 5,00.

Якщо максимум щільності розподілу спостерігається лише для одного значення змінної X (рис. 3.21), розподіл називається унімодальним (одномо-дальним), якщо для декількох несусідніх значень - полімодальний. Мода є природною характеристикою центра групування у разі унімодальних розподілів. Полімодальні розподіли свідчать про суттєву неоднорідність сукупностей. їхнє вивчення доцільне для завдань класифікації об'єктів дослідження.

Для неперервної величини моду Mo[X], як максимум щільності (рис. 3.24),

Пропонуємо порівняти це означення з означенням вибіркової моди мо.

можна визначити за допомогою першої і другої похідної функції за умов монотонності функції щільності на певному проміжку [а, Ь].

Емпіричним аналогом Мо[Х] випадкової величини Х є вибіркова мода Мо - як варіанта, яка найчастіше зустрічається у вибірці.

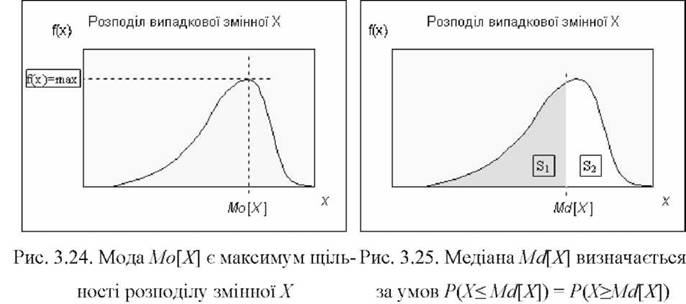
Означення. Медіаною випадкової величини X називають таке її значення МаХ], при якому виконується умова однакових ймовірностей приймати змінною Xзначення, не вище заМаХ] і не нижче МаХ, тобто

Р( Х< МаЩ ) = Р( Х> МаЩ ).

Згідно з геометричною інтерпретацією медіана МаХ - Це точка на абсцисі, через яку площа, що лежить під графіком щільності, ділиться навпіл -на дві рівні частини 8₁=8₂ (рис. 3.25). У разі визначення вибіркової медіани Ма емпіричні дані упорядковуються у варіаційний ряд. Значення середнього елементу цього ряду і є значенням вибіркової медіани (див. розділ 2.2).

Властивості математичного сподівання випадкової величини:

o якщо Х₁, Х₂, Х_п - попарно незалежні випадкові величини (тобто і X, незалежні для і фу ), то математичне сподівання суми дорівнює сумі математичних сподівань цих величин

М[Х₁ + Х₂ + ... + Х_п] = М[Х₁] + ЩХ₂] + ...+МХ_п]; (3.25)

o математичне сподівання добутку незалежних випадкових величин Х₁, Х₂, Х_п дорівнює добуткові математичних сподівання цих величин

M[X_l o X2 o ... o Xn] = M[Xi] o MX₂ o ... oA/LXJ; (3.26)

o математичне сподівання константи дорівнює самій константі

M[a] = a; (3.27)

o математичне сподівання різниці X- M[X] дорівнює нулю

M[X- M[X]] = 0; (3.28)

o якщо незалежні випадкові величини X і Y визначені на тому ж самому просторі елементарних подій, a і b - деякі числа, то

M[aX+bY] = aM[X] + bM[Y]. (3.29)