Математична статистика - Руденко В.М. - 5.4. ПЕРЕВІРКА ГІПОТЕЗ ПРО ЧИСЕЛЬНІ ЗНАЧЕННЯ ПАРАМЕТРІВ

Гіпотези про чисельні значення параметрів зустрічаються тоді, коли необхідно переконатися, що параметри центральних тенденції або мінливості відповідають номіналові. Наприклад, для середнього значення параметру це означає, що необхідно перевірити нульову гіпотезу Н₀: /г = а проти альтернативної ні: /і Ф а, або Н₂: /г > а, або н₃: /і < а. Аналогічні гіпотези можна сформулювати для інших параметрів. У табл. 5.3 приведено варіанти гіпотез, статистичні критерії та умови прийняття рішень для здійснення перевірки гіпотез про чисельні значення параметрів нормального закону розподілу.

Таблиця 5.3.

Критерії перевірки гіпотез про чисельні значення параметрів

Методи перевірки гіпотез про чисельне значення середнього параметра з нормальним законом розподілу поділяються на дві групи: для сукупностей з відомою (г-критерій) і з невідомою дисперсією (і-критерій). Статистика критерію першої групи використовує нормальний розподіл, другої - розподіл Стьюдента (похідний від нормального розподілу). Обидві моделі призначені для даних, виміряних за інтервальною шкалою або шкалою відношень

Значущість середнього (критерій Z, дисперсія відома)

Статистика двобічний г-критерію, коли дисперсія генеральної сукупності відома має вид:

де ¡1 і а² - середнє і дисперсія генеральної сукупності; ц₀ і п - середнє та обсяг вибірки.

Приклад 5.10. Чи можна прийняти на рівні значущості 0,05 середні показники результатів тестування 40 учнів як задовільний прогноз, що не відрізнятиметься від середнього нормативного показника 4,0 при дисперсії 0,4?

Послідовність рішення:

o Ситуації відповідає варіант неспрямованих гіпотез:

Н₀: ц = Цо^; Ні: fi Ф Цо.

o Перевірка припущень: досліджуваний параметр має нормальний розподіл; дисперсія а² відома; виміри зроблено за шкалою інтервалів.

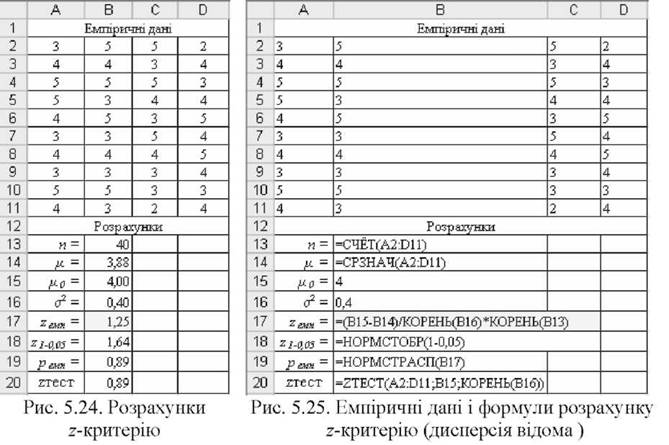
o Результати розрахунку емпіричного z-критерію показано на рис. 5.24, необхідні для цього формули наведено на рис. 5.25.

o Вибіркове середнє показника результатів тестування учнів fi₀ ~ 3,88;

емпіричне значення z-критерію дорівнює

4,0-3,88 і-г , "_г z_eMn = д-f v40 * 1,25.

o Критичне значення z-критерію можна визначити за допомогою функції MS Excel =НОРМСТОБР(1-а), яка у разі двобічної моделі для а=0,05 повертає значення Z_1-0i05 ~ 1,64 (див. комірку В18).

o Прийняття рішення. Оскільки | z | < z_{1-0 05} , тобто |1,25| < 1,64, нульова

гіпотеза H₀ приймається на рівні значущості 0,05.

o Формулювання висновків. На рівні значущості 0,05 відсутні підстави стверджувати про те, що середнє значення відрізняється від нормативного.

Перевірку гіпотези про невідоме значення математичного очікування генеральної сукупності можна провести, якщо визначити ймовірність р_емп, яка відповідає емпіричному критерію z_eMn. Таку перевірку можна виконати за допомогою функції =HOPMCTPACn(z_ejl,"), яка повертає значення р_ем" ~ 0,11 ~ 11% (див. комірку В19). Нульова гіпотеза H₀ відхиляється за умови р_ем"< а. У прикладі ця умова не виконуєтьсяр_ем" ~ 11% > 5%, тому H₀ приймається.

Табличний процесор MS Excel надає можливість перевірки статистичних гіпотез щодо рівня середнього сукупності з нормальним законом розподілу за допомогою функції =ZTECT(), яка повертає значення 1-р_емп. У якості аргументів функції виступають: вибірковий масив, математичне очікування і стандартне відхилення генеральної сукупності (у разі відсутності останньої використовується вибіркова статистика).

Нульова гіпотеза H₀ приймається на рівні значущості а, якщо ZTECT<1-а. У комірку В20 внесено =ZTECT(A2:D11;B15;KOPEHb(B16)) і отримано значення приблизно 0,89 або 89% (див. рис. 5.24 і 5.25). Отже, на рівні значущості 0,05 умова 89% < 95% виконується і H₀ приймається.