Теорія статистики - Мармоза А.Т. - 5.4. Моменти статистичних розподілів

Розглянуті вище середні величини і показники варіації є частковими випадками єдиної системи узагальнюючих статистичних характеристик розподілу, що одержала назву моменту статистичного розподілу.

Моментом розподілу називають середню арифметичну величину з піднесених до заданого степеня відхилень окремих варіант від деякої постійної величини (0, X, х0):

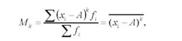
де А - постійна величина, від якої визначаються відхилення (за постійну величину можуть бути взяті нуль, середня арифметична X або умовний початок відліку х0); к - показник степеня, що визначає порядок моменту.

Для вивчення характеристик статистичних розподілів найчастіше використовуються моменти перших п'яти порядків (к дорівнює 0, 1, 2, 3, 4).

Залежно від того, що приймається за постійну величину, від якої визначаються відхилення, розрізняють три види моментів: початкові, центральні та умовні.

Моменти розподілу, при обчисленні яких за вихідну величину приймається нуль (А = 0), називають початковими моментами (М):

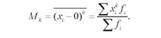
Моменти розподілу, при обчисленні яких за вихідну величину приймаються відхилення від середньої арифметичної (А = X), називають центральними моментами (/г):

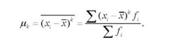
Моменти розподілу, при обчисленні яких за вихідну величину приймаються відхилення від довільно взятої величини (х0), тобто від так званого умовного початку відліку, називають умовними моментами (т):

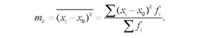
Початкові моменти другого, третього і четвертого порядків так само як і умовні моменти самостійного значення не мають, а використовуються для спрощеного обчислення центральних моментів.

Аналізуючи формули моментів, можна помітити, що початковий момент першого порядку М1 = ^х-^- являє собою середню арифметичну (х) і використовується як показник центру розподілу. Центральний момент першого порядку завжди дорівнює нулю (нульова властивість середньої арифметичної

у (х _ х)2 ї

£ (х( - х) = 0). Центральний момент другого порядку /г2 = '-дорівнює дисперсії. Центральний момент третього порядку ц3 дорівнює нулю в симетричному розподілі і використовується для визначення показника асиметрії (скошеності). Центральний момент четвертого порядку застосовується при обчисленні показника ексцесу (гостровершинності).

В зв'язку з тим, що теоретична форма розподілу найчастіше невідома, викликає інтерес вивчення деяких властивостей кривої, побудованої за даними емпіричного розподілу. Зокрема, велике значення має вимірювання ступеню відхилення даного розподілу від симетричного та характеристика особливості побудови вершини кривої розподілу (ступеня гостровершинності). З цією метою обчислюються показники асиметрії (скошеності) і гостровершинності (ексцесу).

Оскільки моменти залежать від прийнятої системи одиниць, в статистичній практиці виявляється більш доцільним брати не абсолютні значення моментів, а їх відношення до стандартного відхилення (середнього квадратичного відхилення а) у відповідному степені.

За міру асиметрії (скошеності) прийнято розглядати стандартизоване відхилення кт = тобто коефіцієнт скошеності (асиметрії), який являє собою

відношення центрального моменту третього порядку до середнього квадратичного відхилення в третьому степені.

Розрізняють також нормовані моменти, під якими розуміють відношення моменту к-го порядку до середнього квадратичного відхилення в к-му степені. Відповідно до цього коефіцієнт скошеності можна розглядати як третій нормований центральний момент розподілу.

Про наявність асиметрії в досліджуваному розподілі можна судити і за неспівпаданням показників центру розподілу (х і Мо): чим більше між ними різниця, тим більше асиметрія ряду розподілу. Для симетричних розподілів частоти будь-яких двох варіант, рівновіддалених по обидві сторони від центру розподілу, рівні між собою. Розраховані для таких розподілів середня, мода і медіана також рівні.

Одним з найбільш простих показників асиметрії (скошеності), що ґрунтуються на співвідношеннях середньої арифметичної і моди, є показник, запропонований англійським статистиком К. Пірсоном:

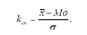
Враховуючи те, що в помірно асиметричному розподілі відстань між показниками центра розподілу характеризується такою рівністю|д- їа | = |о - її |: 3, формула К. Пірсона може бути записана таким чином:

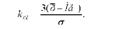
Його величина може бути додатною чи від'ємною. В першому випадку мова йде про правосторонню асиметрію, в другому - про лівосторонню.

При наявності додатної (правосторонньої) скошеності (права гілка кривої довша) між показниками центру розподілу існує таке співвідношення Мо <Ме < х, відповідно при наявності від'ємної (лівосторонньої) скошеності (ліва гілка кривої довша) спостерігається обернене співвідношення: Мо > Ме > х.

Використовують й інші формули для розрахунку коефіцієнта асиметрії. Так, наприклад, швецький математик Ліндберг запропонував оцінювати асиметрію за формулою:

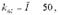
де П - процент одиниць сукупності, у яких значення досліджуваної ознаки перевищує середнє значення по сукупності;

50 - процент варіант, які перевищують середню арифметичну ряду нормального розподілу.

В практичних розрахунках по визначенню асиметрії перевага надається третьому нормованому центральному моменту:

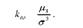
В симетричному ряді розподілу к = 0, при правосторонній скошеності к > 0, при лівосторонній к < 0. Прийнято вважати, що асиметрія вища 0,5 (незалежно від знаку) рахується значною; якщо вона менша 0,25, то незначною.

Застосування цього показника дає змогу не тільки визначити асиметрію, але й відповісти на питання про наявність або відсутність асиметрії в розподілі ознаки в генеральній сукупності. Оцінка суттєвості цього показника дається за допомогою середньої квадратичної помилки, яка залежить від обсягу сукупності і розраховується за формулою:

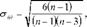
де п - число одиниць сукупності.

Якщо відношення |кю|:ст>3, асиметрія і розподіл ознаки в генеральній сукупності не є симетричним. Якщо відношення кт: а < 3, асиметрія несуттєва, її наявність може бути поясненна впливом різних випадкових обставин.

Для характеристики ступеню гостровершинності (ексцесу) використовується четвертий нормований центральний момент, тобто відношення Лт4.

В нормальному розподілі існує таке співвідношення між центральним моментом четвертого порядку та центральним моментом другого порядку (дисперсією): ц4 = 3ст4 , тобто для нормального розподілу четвертий нормований момент дорівнює 3 ('"у 4 = 3).

Тому дане співвідношення можна використати як міру гостровершинності. Якщо показник гостровершинності (ексцесу) представити у вигляді

Ех = --^ - 3,, то в нормальному розподілі Ео = 0, при гостровершинному або до- сг датному ексцесі Ео> 0 і при плосковершинному або від'ємному ексцесі Ео< 0.

Для визначення ступеня ексцесу (гостровершиності) можна використовувати запропоновану Ліндбергом таку формулу:

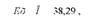
де П - частка (процент) кількості ознак, які знаходяться в інтервалі, що дорівнює половині середнього квадратичного відхилення по той або інший бік від середньої арифметичної;

38,29 - процент кількості варіант, які знаходяться в інтервалі, рівному половині середньо квадратичного відхилення, у загальній кількості варіант ряду нормального розподілу.

Найбільш точним є показник оснований на використанні центрального моменту четвертого порядку:

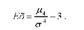
Середня квадратична помилка ексцесу розраховується за формулою:

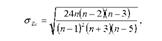
де п - число спостережень.

Якщо відношення Ехі : аА! > 3, то відхилення від нормального розподілу можна вважати суттєвим і навпаки.

Оцінка суттєвості показників асиметрії та ексцесу дає змогу зробити висновок про те, чи можна віднести даний емпіричний розподіл до нормального розподілу.

Обчислимо для досліджуваного ряду розподілу 100 господарств за надоєм молока на корову коефіцієнти скошеності і ексцесу, попередньо визначивши центральні моменти через умовні (табл. 5.5).

Таблиця 5.5. Дані для розрахунку умовних моментів

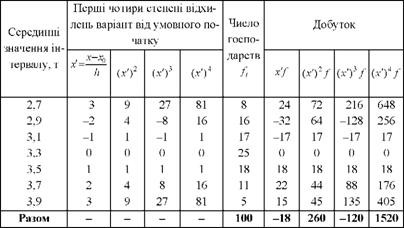
За умовний початок відліку приймемо серединне значення інтервалу з надоєм рівним 3,3 т (х0 = 3,3 т) і який має найбільшу частоту. Величина інтервалу к = 0,2 т.

Використовуючи дані табл. 5.5, визначимо значення моментів відносно початку відліку, виражені в частках інтервалу:

Визначимо значення умовних моментів, виражених у вихідній системі одиниць вимірювання, вносячи при цьому поправку на величину інтервалу у відповідному степені, виходячи зі співвідношення тпк = тп'к ■ кк, де к - порядок моменту (показник степені); к - величина інтервалу;

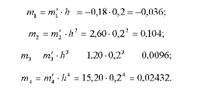
Розрахуємо центральні моменти через умовні, використовуючи формули, взаємозв'язку між моментами:

Визначимо коефіцієнт скошеності (асиметрії):

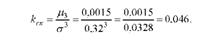
Звідси випливає, що даний ряд розподілу господарств за надоєм молока на корову близький до симетричного, але має невелику додатню скошеність. Розрахуємо коефіцієнт гостровершинності (ексцесу):

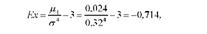
Тобто досліджуваний ряд розподілу характеризується істотною плосковершинністю побудови вершини кривої розподілу.

Визначивши комплекс середніх величин і показників варіації, ми отримали систему статистичних характеристик, які дають можливість всебічно описати досліджуваний ряд розподілу і зробити загальні висновки.

Випишемо основні статистичні характеристики ряду розподілу 100 господарств за надоєм молока на корову, ц:

середня арифметична х = 32,64;

мода Мо = 33,07;

медіана Ме = 32,72;

розмах варіації Я = 14,0;

середнє лінійне відхилення І = 2,6;

дисперсія ст2 = 10,27;

середнє квадратичне відхилення а = 3,2;

коефіцієнт скошеності к" = 0,046;

коефіцієнт гостровершинності Ех = -0,714.

Аналіз наведених статистичних характеристик дає змогу зробити загальний висновок щодо форми розподілу 100 господарств за надоєм молока на корову: досліджуваний ряд є майже симетричним, незначно додатньо скошеним і плосковершинним; розподіл за формою близький до нормального. Однак доведення цього положення потребує спеціальної статистичної оцінки близькості досліджуваного ряду розподілу нормальному на основі відповідних критеріїв. Одержані характеристики ряду розподілу є лише попередніми оцінками відповідних характеристик генеральної сукупності і тому потрібна оцінка їх надійності. Ці питання розглядаються в наступних розділах підручника.