Теорія статистики - Мармоза А.Т. - Розділ 6. Вибіркове спостереження

6.1. Поняття вибіркового спостереження та його теоретичні основи

Як зазначалось у розділі 2, за ступенем охоплення одиниць досліджуваної сукупності статистичне спостереження може бути суцільним і несуцільним.

Суцільне спостереження передбачає обстеження усіх без винятку одиниць генеральної сукупності. Наприклад, для визначення загальної чисельності населення під час перепису збирають дані про кожну окрему людину, яка проживає в країні, для встановлення обсягу виробленої продукції (зерна, молока, м'яса тощо), ведуть щоденний облік її виходу і т. д.

Проте з деяких причин (великої трудомісткості, тривалості проведення, високої вартості тощо) суцільне спостереження часто буває економічно недоцільним або практично нездійсненним. Тому на практиці переважно застосовують несуцільне спостереження, різновидом якого є вибіркове.

Вибірковим спостереженням в статистиці називають такий вид спостереження, який дає можливість зробити висновок про всю сукупність одиниць при обстеженні тільки її частини. Прикладом вибіркового спостереження може бути вибіркове обстеження умов життя домогосподарств, визначення втрат урожаю, якості продукції, польові досліди тощо.

Сукупність методів математичної статистики, що застосовуються для обґрунтувань та висновків при проведенні вибіркового спостереження, називають вибірковим методом.

Вибіркове спостереження є одним з видів несуцільного спостереження, що найбільш широко застосовується. Вибірковими даними користуються досить широко в різних сферах суспільного життя. Наприклад, для оцінки якості сільськогосподарської продукції (зерна, молока тощо) немає необхідності в дослідженні всього обсягу продукції, для цього досить лише взяти певну кількість проб.

Вибіркове дослідження одержало широке поширення в державній і відомчій статистиці. В статистичній практиці вибіркове спостереження застосовується для обстеження умов життя домогосподарств, житлових умов сімей робітників і службовців, їх заробітної плати, цін на ринках, в науковій роботі при статистичній обробці результатів дослідження, для вивчення і контролю якості продукції, громадської думки тощо.

В сільському господарстві вибіркове спостереження застосовується для визначення якості продукції, втрат урожаю, засміченості посівів, схожості, вологості, засміченості зерна, використання робочого часу, контрольних перевірок перепису худоби тощо.

При дотриманні правил наукової організації обстеження вибіркове спостереження дає досить точні результати, тому його часто застосовують для уточнення даних суцільного обліку. Так, при проведенні перепису населення організовують вибіркові контрольні обходи для перевірки правильності записів суцільного спостереження, під час перепису (обліку) худоби на основі вибіркових даних визначають процент недообліку худоби у населення та ін.

В деяких випадках вибіркове спостереження використовують для дослідження процесів і явищ, суцільне спостереження яких недоцільне внаслідок занадто великого обсягу робіт, наприклад обстеження сімейних бюджетів, реєстрація цін на ринках, вивчення споживчого попиту населення тощо.

У проведенні ряду досліджень вибіркове спостереження є єдино можливим, наприклад при контролі якості продукції, якщо перевірка супроводжується знищенням або псуванням зразків, що обстежуються (визначення жирності молока, схожості зерна, міцності тканин на розрив, тривалості горіння електричних ламп тощо).

Широкому використанню вибіркового спостереження в статистичній практиці сприяє сучасна обчислювальна техніка, яка дає змогу значно ускладнити процедури обробки вихідної інформації, а тому підвищити надійність статистичних показників, що одержують за даними вибірки.

З усіх видів несуцільного спостереження головним є вибіркове спостереження, оскільки тільки дані цього спостереження дають змогу науково-обгрунтовано і з необхідною вірогідністю поширити дані, одержані по частині сукупності на всю сукупність.

Науково організоване вибіркове спостереження має ряд суттєвих переваг перед суцільним.

1. Економія трудових, матеріальних ресурсів і коштів за рахунок скорочення обсягів робіт по збиранню, обробці і узагальненні даних. Наприклад, якщо вибірці підлягає 10% загальної чисельності одиниць, то обсяг робіт скорочується порівняно з суцільним обстеженням в 10 разів.

2. Проведення спостереження у стислі строки і за більш широкою програмою, одержання кінцевих результатів дослідження в коротші строки.

3. Зведення до мінімуму псування або навіть знищення досліджуваних зразків при перевірці їх якості.

4. Досягнення більшої точності результатів спостереження завдяки скороченню помилок, що виникають при реєстрації. В процесі проведення вибіркового спостереження необхідно дати правильне уявлення про зведені показники всієї сукупності на основі обстеження її частини при умові дотримання всіх вимог і принципів проведення статистичного спостереження і науково організованої роботи по відбору одиниць.

Сукупність відібраних для обстеження одиниць прийнято називати вибірковою, а сукупність одиниць, з якої проводиться відбір, - генеральною.

Властивість вибіркової сукупності відтворювати генеральну сукупність дістала назву репрезентативності, що означає представництво з певною точністю і вірогідністю. В зв'язку з тим, що при вибірковому спостереженні обстежується тільки частина одиниць генеральної сукупності, то характеристики вибіркової сукупності, як правило, відрізняються від характеристик вибіркової сукупності, тобто мають місце так звані помилки репрезентативності (відповідності, відображення).

Тому одним із основних завдань вибіркового методу є одержання таких вибіркових характеристик, які б якомога точніше відтворювали характеристики генеральної сукупності, тобто давали найменші помилки репрезентативності.

Об'єктивну гарантію репрезентативності одержаної вибіркової сукупності дає застосування відповідних науково обґрунтованих способів відбору одиниць, що підлягають обстеженню. В процесі формування вибіркової сукупності має бути забезпечений строго об'єктивний підхід до відбору одиниць, що гарантує рівну можливість кожній одиниці генеральної сукупності потрапити у вибірку. Кількість відібраних при цьому одиниць має бути досить великою.

Мета вибіркового спостереження полягає в тому, що на основі відібраних з генеральної сукупності для обстеження одиниць необхідно дати оцінку невідомим параметрам генеральної сукупності.

Теоретичною основою вибіркового методу є математичні теореми закону великих чисел, викладення яких дається в курсі математичної статистики і теорії ймовірностей.

Великий внесок в розробку теоретичних основ вибіркового методу внесли Я.Бернуллі, С.Пуассон, К.Пірсон, Р.Фішер, В.Госсет. П.Л.Чебишев, О.М.Ляпунов та ін. Нерівність П.Л.Чебишева стосовно вибіркового методу може бути сформульована так: при необмеженому збільшенні числа незалежних спостережень (п -"со) в генеральній сукупності з обмеженою дисперсією з імовірністю як завгодно близькою до одиниці можна очікувати, що відхилення вибіркової середньої від генеральної середньої буде як завгодно мале, тобто

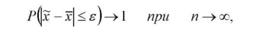
де Р - імовірність нерівності, що стоїть у дужках; є - будь-яке завгодно мале додатне число; х і х - вибіркова і генеральна середня.

На основі теорем закону великих чисел розв'язуються два взаємопов'язаних і важливих в практичному відношенні питання вибіркового спостереження: розрахунок необхідної чисельності вибірки і визначення помилок вибірки при заданому рівні довірчої імовірності.

Результати вибіркового спостереження характеризуються середніми і відносними узагальнюючими показниками. Узагальнюючі показники генеральної сукупності (середня, частка, дисперсія та ін.) називають генеральними, а відповідні узагальнюючі показники вибіркової сукупності -вибірковими.

У вибірковому спостереженні прийняті такі позначення. Обсяг генеральної сукупності позначають через N а вибіркової - через п. Середню величину і дисперсію ознаки в генеральній сукупності називають генеральною середньою і генеральною дисперсією. Генеральну середню позначають через X, а генеральну дисперсію - через <зг.

Середню величину і дисперсію ознаки у вибірковій сукупності називають вибірковою середньою і вибірковою дисперсією. Вибіркову середню позначають через х , а вибіркову дисперсію - через ст2.

Частку одиниць, що володіють даною ознакою в генеральній сукупності, називають генеральною часткою. Відносна величина частки, що одержана в результаті вибіркового спостереження, називається вибірковою часткою або частістю. Частість показує, яка частка одиниць вибіркової сукупності володіє досліджуваною ознакою. Генеральну частку позначають через р, а частість - через со.

Наведемо приклад розрахунку зазначених показників для генеральної і вибіркової сукупності. Припустимо, що з 300 однакових за площею ділянок посіву, але з різною урожайністю ячменю, що представляють генеральну сукупність, відібрано у випадковому порядку 30 ділянок (10% всіх ділянок), що становлять вибіркову сукупність (табл. 6.1).

Таблиця 6.1. Урожайність ячменю і число ділянок генеральної і вибіркової сукупностей

Визначимо за цими даними середню урожайність, дисперсію і частку ділянок з урожайністю 25 ц/га і більше для генеральної і вибіркової сукупностей: а) для генеральної сукупності середня урожайність

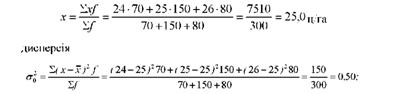
частка ділянок з урожайністю 25 ц/га і більше

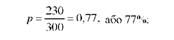
б) для вибіркової сукупності

частка ділянок з урожайністю 25 ц/га і більше

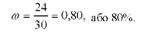
Отже, генеральна середня становить 25,0 ц/га, генеральна дисперсія -0,50, а генеральна частка - 0,77, відповідно вибіркова середня - 25,1 ц/га, вибіркова дисперсія - 0,49. вибіркова частість - 0,80. Як видно, ті самі показники генеральної і вибіркової сукупностей не збігаються. В абсолютному виразі різниця між середніми становить 0,1 ц/га, між частками - 0,03. Незначні розбіжності між середніми і відносними показниками свідчать проте, що вибіркова сукупність досить точно репрезентує генеральну сукупність.