Теорія статистики - Мармоза А.Т. - 6.3. Способи формування вибіркових сукупностей

Результати вибіркового спостереження багато в чому залежать від способів формування та відбору одиниць у вибіркову сукупність. Основним принципом правильності відбору одиниць є строго об'єктивний підхід до відбору одиниць для спостереження. Дотримання цього принципу дає змогу запобігти систематичних (тенденційних) помилок і найбільш точно і повно представити генеральну сукупність.

Попередження систематичних помилок досягається в результаті застосування науково-обгрунтованих способів формування вибіркової сукупності.

При формуванні вибіркової сукупності мають бути забезпечені дві умови:

1) рівні можливості для кожної одиниці генеральної сукупності потрапити у вибірку (так званий принцип рівноможливості);

2) досить представницька чисельність вибіркової сукупності.

В статистиці застосовуються різні види і способи формування вибіркової сукупності. В кожному конкретному випадку залежно від цілого ряду умов, а саме завдань дослідження, суті досліджуваного явища, специфіки об'єкта, обсягу сукупності, коливання ознаки, наявності матеріальних і трудових ресурсів, вибирають найбільш оптимальну систему формування вибіркової сукупності, яка визначається видом і способом відбору.

За видами розрізняють: 1) індивідуальний відбір - у вибірку потрапляють окремі одиниці генеральної сукупності; 2) груповий відбір - у вибірку потрапляють якісно однорідні групи або серії досліджуваних одиниць; 3) комбінований відбір як комбінація індивідуального і групового відбору.

Спосіб відбору визначає конкретний механізм або процедуру вибірки одиниць з генеральної сукупності. В практиці застосування вибіркового спостереження найбільше поширення одержали такі види вибірки: власне-випадкова, механічна, типова, серійна (гніздова) і комбінована. Ці способи можуть бути застосовані і в поєднанні один з одним.

При власне-випадковій вибірці відбір одиниць з генеральної сукупності проводиться без попереднього розчленування її на будь-які групи і одиниця спостереження збігається з обліковою одиницею.

Суть випадкового відбору полягає в тому, що кожна одиниця спостереження потрапляє у вибірку випадково - за жеребом. Залежно від способу відбору одиниць розрізняють повторний і безповторний відбір.

При повторному відборі (за схемою поверненого шару) кожна одиниця після її реєстрації повертається до генеральної сукупності і знову може бути відібраною. Цей спосіб відбору забезпечує постійність складу генеральної сукупності. Імовірність потрапляння кожної одиниці до вибірки залишається постійною, отже, зберігається незалежність наступного витягання одиниць від попередніх.

При безповторному відборі (за схемою неповерненок) шару) кожна одиниця після її реєстрації до генеральної сукупності не повертається і в подальшому відборі участі не бере, тобто та сама одиниця не може двічі потрапити до вибірки. Тому безповторна вибірка краще репрезентує генеральну сукупність і, отже, дає меншу помилку, ніж повторна.

На відміну від повторного відбору при безповторному відборі не зберігається постійність генеральної сукупності, а імовірність потрапляння окремих одиниць до вибірки весь час змінюється (для одиниць, що залишилися, вона зростає). В зв'язку з цією особливістю до формул середньої та граничної помилок вибірки вводиться поправочний коефіцієнт, про що вже згадувалось вище.

Щоб позбутися елементів суб'єктивності при відборі одиниць з генеральної сукупності можна користуватися таблицею випадкових чисел.

Випадковий відбір дає добрі результати в однорідних сукупностях, тобто в тих, де варіація ознаки є незначною. Якщо ж сукупність неоднорідна і складається з різних типів явищ, то необхідно застосувати типову вибірку.

Механічний відбір - це різновидність випадкового відбору. Суть його полягає в тому, що всі одиниці генеральної сукупності розташовуються в певному порядку (за зростанням або зменшенням, за алфавітом, географічним положенням тощо), а потім суто механічно через певний інтервал відбираються одиниці у вибіркову сукупність.

Наприклад, якщо треба відібрати 100 об'єктів із генеральної сукупності чисельністю 1000 одиниць, то величина інтервалу становитиме к = N: п = 1000: 100 = 10, тобто слід відібрати по одній одиниці з кожного десятка. Щоб забезпечити випадковість відбору доцільно першу вибірку з першого інтервалу провести за жеребом. Якщо відбір починають з третього об'єкта, то до вибірки потраплять 3-й, 13-й, 23-й і т.д. об'єкти.

Середню і граничні помилки вибірки при механічному відборі розраховують за тими самими формулами, що і для випадкового безповторного відбору, оскільки механічний відбір, як правило, проводиться безповторно.

При типовому відборі всю генеральну сукупність попередньо поділяють на типові групи за досліджуваною ознакою, а потім із кожної групи випадковим або механічним способом відбирають необхідну кількість одиниць. При цьому до початку відбору необхідно забезпечити принцип пропорційного представництва кожної групи відповідно з їхньою чисельністю або їхніх середніх квадратичних відхилень або дисперсій. Можливий також відбір, пропорційний обом показникам - чисельності одиниць в типових групах і ступеню варіації ознаки. Такий відбір називається оптимальним. На практиці найчастіше застосовують вибірку, пропорційну чисельності типових груп.

Розчленування сукупності на типові групи дає можливість усунути вплив міжгрупової (систематичної) варіації на результати вибірки, оскільки у вибірці забезпечується представництво всіх груп, що може не мати місця при випадковому відборі. Отже, самою вибіркою відтворюється (відображується) міжгрупова варіація. Залишається варіація вибіркових даних навколо середніх (внутрішньогрупова або залишкова варіація), яку визначають по кожній із виділених типових груп.

Тому розмір середньої помилки вибірки буде визначатись тільки величиною внутрішньогрупової (залишкової) варіації (&1.ір) ознаки, яка менша від загальної на величину міжгрупової варіації. Залишкову дисперсію обчислюють як середню арифметичну зважену із середніх квадратів відхилень, які вимірюють залишкову варіацію в кожній групі.

Середня помилка типової вибірки розраховується за формулою:

Наведемо формули граничних помилок вибірки для вибіркової середньої і частки для типової вибірки:

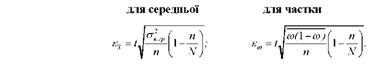
Типовий відбір дає точніший результат порівняно з випадковим або механічним відбором, оскільки розчленуванням сукупності на типові групи забезпечується потрапляння до вибірки одиниць від усіх виділених груп і типів.

Суть серійного відбору полягає в тому. що відбору підлягають не окремі одиниці генеральної сукупності, а цілі серії таких одиниць. У відібраних методом випадкового безповторного або механічного відбору серіях проводять суцільний опис усіх одиниць, що до них увійшли. При цьому загальне число серій, які складають генеральну сукупність, розглядають як її загальну чисельність Nc, а кількість відібраних - як обсяг вибірки пс.

Оскільки при серійному способі формування вибіркової сукупності кожна серія виступає як самостійна одиниця спостереження, то варіація усередині серій (внутрішньосерійна, аг,£) при розрахунку середньої помилки має бути виключена. Отже, середня помилка вибірки у цьому випадку залежить тільки від міжсерійної варіації о"*,,:

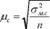
Формули граничних помилок вибірки для середньої і для частки при серійному відборі матимуть вигляд:

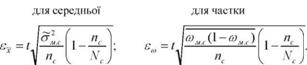
Комбінований відбір.

Розглянуті способи вибірки на практиці застосовуються не тільки самостійно, але і в комбінуванні в різних поєднаннях і з різною послідовністю. Так, наприклад, можна комбінувати серійний відбір з власне випадковою вибіркою. При цьому генеральна сукупність спочатку поділяється на серії і відбирається необхідне число серій, а далі у відібраних серіях проводиться випадковий відбір одиниць у вибіркову сукупність. Можлива також комбінація типової і серійної вибірки, коли серії відбираються в установленому порядку з кількох типових груп.

Розрізняють також одноступінчастий і багатоступінчастий способи відбору одиниць у вибіркову сукупність.

При одноступінчастій вибірці кожна відібрана одиниця зразу ж підлягає вивченню. Так обстежують одиниці вибіркової сукупності при власне-випадковій вибірці.

При багатоступінчастій вибірці спочатку проводять відбір з генеральної сукупності окремих груп, а потім з відібраних груп формують вибірку другого, третього і т.д. порядку, яку й аналізують.

В статистичній практиці найбільш широке застосування одержали двоступінчаста і триступінчаста вибірки. Прикладом двоступінчастої вибірки може бути аналіз якості насіння, при якому спочатку відбирають проби з партії насіння, а потім з відібраних проб виділяють наважку для визначення його якості (схожості, чистоти та інших посівних якостей насіння). Прикладом триступінчастої вибірки є відбір сімей для бюджетного обстеження, при якому на першій стадії з врахуванням виробничого напрямку відбирають райони, на другій - підприємства, і, насамкінець, на третій - окремі сім'ї.

Багатоступінчаста вибірка дає, як правило, менш точні результати порівняно з одноступінчастою, оскільки її помилки складаються з помилок на окремих ступенях відбору. Однак на практиці, якщо одноступінчату вибірку організувати складно, використовують багатоступінчасту вибірку.

Кінцевою метою вибіркового спостереження є характеристика генеральної сукупності на основі даних одержаних за вибіркою і поширення цих даних на всю сукупність. При цьому вибіркові середні і відносні показники мають бути поширені на генеральну сукупність з урахуванням граничних можливих помилок вибірки.

Існує два способи такого поширення: 1) спосіб прямого перерахування; 2) спосіб поправочних коефіцієнтів.

Суть способу прямого перерахування полягає в перемноженні середнього значення ознаки знайденого в результаті вибіркового спостереження на число одиниць генеральної сукупності. Припустимо, що при вивченні шерстної продуктивності овець вибірковим спостереженням в особистих підсобних господарствах населення було встановлено, що середній настриг на вівцю становив 3,0 кг. Знаючи, що в господарствах населення є 2000 овець, можна способом прямого перерахування дістати величину валового настригу вовни; 3,0 o 2000 = 6000 кг, або 6,0 т. Якщо при цьому відомо, що гранична помилка вибірки з імовірністю Р = 0,95 дорівнює 0,1 кг і, отже, генеральна середня з такою ж імовірністю коливається в межах від 2,9 до 3,1 кг, то загальний валовий настриг вовни буде коливатись від 5,8 до 6,2 т.

Спосіб поправочних коефіцієнтів застосовується у випадках, коли метою вибіркового спостереження є уточнення результатів суцільного спостереження. При уточнені даних суцільного спостереження на основі вибіркового спостереження визначається так званий поправочний коефіцієнт, яким і користуються для внесення поправок в дані суцільного спостереження. Припустимо, що за даними суцільного спостереження в господарствах населення зареєстровано 1500 корів. Контрольними обходами було охоплено 10% дворів, де зареєстровано 160 корів, а за даними суцільного спостереження числилось 155 корів. Поправочний коефіцієнт становитиме (160:155)400=1,0322, або 103,22%. Таким чином, недооблік корів при суцільному спостереженні становив 3,22%, а фактична чисельність корів в господарствах населення з поправкою на недооблік становить: 1500 o 1,0322 = 1548 корів.