Теорія статистики - Мармоза А.Т. - 6.7. Малі вибірки

Розглянуті вище прийоми розрахунку характеристик вибіркової сукупності (дисперсії, середньої і граничної помилок тощо) передбачають досить велику чисельність вибірки (п > 30). В той самий час не завжди можливий і доцільний великий обсяг вибірки. У практиці виробничих спостережень та в науково-дослідній роботі часто доводиться користуватися невеликими за обсягом вибірками, чисельність яких не перевищує 30 одиниць (агрономічні і зоотехнічні досліди, перевірка якості продукції, пов'язана зі знищенням зразків тощо). В статистиці вони дістали назву малих вибірок. Відповідно вибірки з чисельністю більше 30 одиниць називають великими вибірками.

Невеликий обсяг вибірки зменшує її точність порівняно з великою вибіркою. Проте доведено що результати, які отримані за малими вибірками, також можна поширювати на генеральну сукупність. Але тут необхідно враховувати деякі особливості, зокрема, при розрахунку середнього квадратичного відхилення. При малому обсязі вибірки слід користуватися незміщеною оцінкою дисперсії 52.

Основи теорії малих вибірок розробив англійський математик-статистик В.Госсет (псевдонім Стьюдент). Дослідження Стьюдента показали, що при невеликій чисельності сукупності середнє квадратичне відхилення у вибірці значно відрізняється від середнього квадратичного відхилення в генеральній сукупності.

Оскільки середнє квадратичне відхилення генеральної сукупності є одним із параметрів кривої нормального розподілу, то використовувати функцію нормального розподілу для оцінки параметрів генеральної сукупності за даними малих вибірок в силу отримання великих помилок неправомірно.

При розрахунку середньої помилки по вибірках малої чисельності завжди треба користуватись незміщеною оцінкою дисперсії

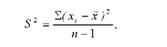
де п - 1 - число ступенів свободи варіації (к), під яким розуміють число одиниць, здатних приймати довільні значення, не змінюючи їх загальної характеристики (середньої).

Наприклад, проведено три спостереження: х1 = 4; х2 = 2; х3 = 6. Середня величина

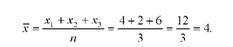
Отже, вільно варіюючих величин залишається тільки дві, тому що третя може бути знайдена за відомими двома величинами і середньою:

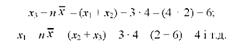
Отже, для даного прикладу число ступенів свободи варіації дорівнює 2 (к = п - 1 = 3 - 1 = 2).

Стьюдент обґрунтував закон розподілу відхилень вибіркових середніх від генеральної середньої для малих вибірок. Згідно розподілу Стьюдента імовірність того, що гранична помилка не перевищить і-кратну середню помилку в малих вибірках залежить від величини і і чисельності вибірки.

Теоретичне нормоване відхилення для малих вибірок одержало назву і-критерію на відміну від і-критерію нормального розподілу, який застосовується у великих вибірках. Значення і-критерію Стьюдента наводяться в спеціальних таблицях (дод. 3).

Розглянемо порядок визначення середньої і граничної помилки для малої вибірки на такому прикладі. Припустимо, для визначення величини втрат при збиранні картоплі проведено перекопування п'яти випадково відібраних площадок по 4 м2. Втрати по площадках становили (кг); 0,6; 0,2; 0,8; 0,4; 0,5.

Середня величина втрат

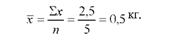
Судячи за окремими спостереженнями, величина втрат сильно варіює і середня лише по п'яти спостереженнях може мати велику помилку.

Для розрахунку помилок вибірки визначимо незміщену оцінку дисперсії

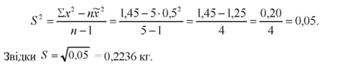
Розрахуємо середню помилку вибіркової середньої, де замість середнього квадратичного відхилення використовується його незміщена оцінка:

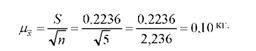
За таблицями Стьюдента (дод. 3) встановимо, що при довірчій імовірності Р = 0,95 (рівень значущості а = 0,05) і при к = п - 1 = 5 - 1 = 4 ступенях свободи варіації і = 2,78. Тоді гранична помилка вибірки дорівнює

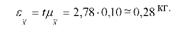
Отже, з імовірністю Р = 0,95 можна стверджувати, що величина втрат на всьому полі становитиме 0,5 ± 0,28 кг, або від 0,22 до 0,78 кг з розрахунку на 4 м2.

Як бачимо з прикладу, межі випадкових коливань при малих вибірках досить великі і можуть бути скорочені за рахунок збільшення чисельності вибірки і зменшення коливання (дисперсії) ознаки.

Якщо б ми використали для розрахунку довірчих меж генеральної середньої таблицю інтегралу імовірностей (дод. 2), то і було б рівним 1,96 і єх = іИзі = 1,96 o 0,10 = 0,20 кг, тобто довірчий інтервал був би вужчим (від 0,30 до 0,70 кг).

Малі вибірки в силу своєї невеликої чисельності навіть при найретельнішій організації спостереження не відображають достатньо точно показники генеральної сукупності. Тому результати малих вибірок рідко використовуються для встановлення надійних меж, в яких знаходяться характеристики генеральної сукупності.

Критерій Стьюдента застосовується головним чином для перевірки статистичних гіпотез щодо істотності відмінностей між показниками двох або кількох малих вибірок (див. розділ 7).