Теорія статистики - Мармоза А.Т. - 7.5. Перевірка статистичних гіпотез щодо розподілів

Поряд з перевіркою статистичних гіпотез щодо середніх інколи потрібно перевірити гіпотези щодо характеру розподілу. Гіпотези про розподіли полягають в тому, що розподіл в генеральній сукупності підпорядковується якому-небудь певному закону. Перевірка гіпотези полягає в тому, щоб на основі порівняння фактичних (емпіричних) частот з передбачуваними (теоретичними) частотами зробити висновок про відповідність фактичного розподілу гіпотетичному розподілу.

Процедура перевірки гіпотези про відповідність емпіричного розподілу теоретичному складається з таких етапів:

1. Обчислення оцінок параметрів передбачуваного розподілу на основі даних вибіркового спостереження.

2. Визначення теоретичних частот на основі одержаних оцінок параметрів, виходячи з теоретичної функції частот.

3. Оцінка близькості емпіричного розподілу теоретичному на основі певного критерію згоди.

Оскільки нормальний розподіл зустрічається досить часто, то найчастіше перевіряють гіпотези про відповідність вибіркового розподілу нормальному. Однак, поряд з нормальним розподілом генеральні сукупності можуть бути розподілені і за іншими законами. Тому вибір теоретичного закону розподілу повинен базуватись на глибокому розумінні характеру формування досліджуваного явища або процесу. Певну роль у вирішенні цього питання може відігравати розрахунок статистичних характеристик вибіркових розподілів і побудова графіків (гістограми, полігону, кумуляти тощо). Так, про форму розподілу роблять висновок за вибірковими коефіцієнтами скошеності і ексцесу: якщо вони рівні нулю або близькі до нуля, то можна припустити, що досліджуваний розподіл належить до нормального; якщо середня арифметична та дисперсія рівні, або дуже близькі одна до одної, то можна припустити, що вибірковий розподіл відповідає розподілу Пуассона.

Для перевірки гіпотези щодо відповідності вибраних законів розподілу (нормальне, біноміальне, Пуассона тощо) розподілу в генеральній сукупності в більшості випадків при розрахунку критеріїв згоди використовуються відхилення емпіричних частот від теоретичних. Чим менше це відхилення, тим точніше теоретичний розподіл відтворює вибірковий та навпаки.

При перевірці статистичних гіпотез відносно розподілів може бути використано ряд критеріїв. З множини критеріїв згоди, які використовуються при перевірці гіпотез щодо розподілів найчастіше за інші застосовують найпотужніший параметричний критерій Пірсона (%2 - хі-квадрат). Його обчисляють як суму частки від ділення квадрату різниці між емпіричними і теоретичними частотами на теоретичні частоти:

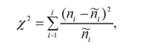
де l - число інтервалів (класів, груп) на які розбито вибірковий розподіл; ni -частоти емпіричного розподілу; ni - частоти теоретичного розподілу.

З формули випливає, що чим менше розбіжність між п і п , тим ближче за значенням один до одного емпіричні та теоретичні частоти, тим менше %2. При повному збігу теоретичних і вибіркових частот %2 = 0, у протилежному випадку %2 > 0. Область зміни %2 від 0 до <ю. При великому числі ступенів свободи (к-"<ю) розподіл %2 набуває форми, близької до нормального розподілу.

Щоб оцінити близькість емпіричного і теоретичного розподілів необхідно розрахувати фактичне значення %2 і порівняти його з табличним значенням при заданому рівні значущості (а) і відповідному числі ступенів свободи к.

Число ступенів свободи визначають по-різному залежно від характеру перевіряємо! гіпотези та особливостей вихідної інформації. Так, якщо перевіряється гіпотеза про узгодженість вибіркового і теоретичного розподілів, то число ступенів свободи визначають за формулою

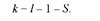
де І - число інтервалів (класів, груп) вибірки; 5 - число параметрів генерального розподілу, які оцінюються за даними вибірки.

При оцінці відповідності емпіричного розподілу нормальному число ступенів свободи к = І -1 - 2 = 1-3, оскільки для побудови кривої нормального розподілу оцінюються два параметри: середня арифметична і середнє квадратичне відхилення. Якщо перевіряється відповідність вибіркового розподілу Пуассона, то оцінюється один параметр X. Тоді число ступенів свободи к = І - 1 - 1 = І - 2.

Якщо вихідні дані подано у вигляді таблиці розподілу частот і необхідно перевірити гіпотезу щодо незалежності розподілу двох ознак, то число ступенів свободи визначають за формулою:

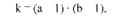
де а - число рядків; Ь - число стовпців.

Так, число ступенів свободи к = (а - 1) o (Ь - 1) = (2 - 1) х (2 - 1) = 1 для таблиці 2 х 2, к = 4 для таблиці 3 х 3, к =2 для таблиці 3 х 2 і т.д.

Якщо перевіряється гіпотеза щодо однорідності двох сукупностей, то число ступенів свободи визначають за формулою к = п - 1, де п - число інтервалів (класів, груп).

Як видно, для всіх випадків число ступенів свободи крім обов'язкових обмежень завжди зменшується на одиницю, тобто має місце один лінійний обмежуючий зв'язок - рівність сум емпіричних і теоретичних частот.

Якщо отримане за вибіркою значення Хфакт - Ха, то нульова гіпотеза приймається. Якщо ж Хфакт > Ха, т0 нульова гіпотеза відхиляється.

Фактичне значення можна обчислити і за іншою формулою, яка випливає з вище наведеної:

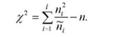
Ця формула не потребує обчислення квадратів відхилень (в чому полягає її простота), її можна використовувати і для перевірки правильності обчислень.

Якщо вихідні дані подано у вигляді чотирьох клітинної таблиці розподілу частот за двома ознаками (2 х 2) з чисельностями пі:

то фактичне значення %2 може бути визначене за формулою:

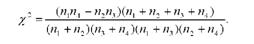
^2 критерій Пірсона використовується для розв'язування ряду задач, зокрема, при перевірці гіпотез про згоду (відповідність) вибіркового і теоретичного розподілів, про незалежність розподілів, про однорідність сукупностей. Стосовно цих задач критерій %2 називають критерієм згоди, незалежності і однорідності.

Застосування критерію %2 вимагає дотримання ряду умов, найважливішими серед яких є:

1) обсяг вибірки повинен бути досить великим (при п < 50 потужність критерію %2 значно знижується);

2) чисельність окремих інтервалів (класів) має бути не менше п'яти одиниць. Якщо ця умова не виконується, то проводиться об'єднання малочисельних інтервалів з числом одиниць менше 5 (як виняток таких інтервалів може бути не більше 20% від їх загальної кількості);

3) частоти не можна перетворювати в частки, так як це може призвести до збільшення величини відхилень п - п .

Розглянемо приклад перевірки статистичної гіпотези про відповідність емпіричного розподілу нормальному. Для цього використаємо дані ряду розподілу 100 господарств за надоєм молока на корову (табл. 4.2).

Розрахунок характеристик варіаційного ряду розподілу 100 господарств за надоєм молока (моди, медіани, коефіцієнтів скошеності та ексцесу) показав, що емпіричний розподіл дуже близький до симетричного і характеризується такими параметрами:

1. середній надій на корову х = 32,6 ц;

2. вибіркове середнє квадратичне відхилення ег= 3,2 ц;

3. величина інтервалу к = 2,0 ц;

4. чисельність вибіркової сукупності п = 100. Розглянемо всі етапи процедури перевірки гіпотези.

1. Сформулюємо нульову і альтернативну гіпотези: Н0; емпіричний розподіл відповідає нормальному; На : емпіричний розподіл не відповідає нормальному.

2. Приймемо рівень значущості а = 0,05.

3. Найпотужнішим критерієм перевірки цієї гіпотези є %2 - критерій згоди Пірсона.

4. Для перевірки Н0 необхідно розрахувати %2 і порівняти його з табличним значенням Ха.

Спочатку необхідно, виходячи із припущення про відповідність емпіричного розподілу нормальному побудувати теоретичний розподіл (криву нормального розподілу), для побудови якого використаємо параметри вибіркового розподілу х = 32,6 ц; 8 = 3,2 ц.

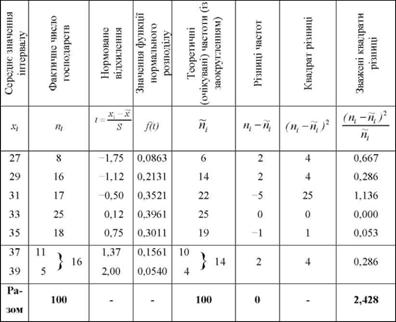
5. Порядок розрахунку теоретичних частот нормального розподілу і критерію %2 наведено в табл. 7.4.

6. Дамо деякі пояснення до розрахунків. Значення нормованого відхилення .,■ визначається як ---, де за приймається серединне значення інтервалу.

Виражаючи довжину інтервалу к також в одиницях середнього

Таблиця 7.4. Розрахунок теоретичних частот нормального розподілу і критерію

к

квадратичного відхилення як ^ при відомому обсязі вибірки п, можна розрахувати теоретичні (очікувані) частоти для будь-якого інтервалу, використовуючи таке співвідношення:

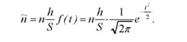
Значення функції нормального розподілу /(і) знайдемо за таблицею (дод. 1)

Значення постійного виразу п ^ для даної задачі становитиме

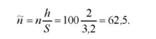
Тоді теоретичні частоти пі нормального розподілу становитимуть: для першого інтервалу 62,5 o 0,0863 = 6; для другого інтервалу 62,5 o 0,2131 = 14 і т.д.

Інтервали з числом одиниць менше 5 необхідно об'єднати. Тому два останніх інтервали укрупнимо. Підрахуємо суми теоретичних і фактичних частот і перевіримо їх рівність загальному підсумку (п = 100).

7. Обчислимо фактичне значення критерію %2. Послідовність обчислення %2 наведена в трьох останніх колонках табл. 7.4.

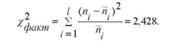
Такий самий результат дістанемо за іншою формулою

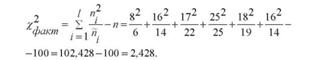
8. Для встановлення табличного значення %2 необхідно визначити число ступенів свободи к. Визначимо його як число інтервалів (груп, класів, з врахуванням укрупнення) без одиниці і мінус дві постійні величини, які описують криву нормального розподілу (~ і а):

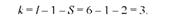
За таблицею (дод. 6) при а = 0,05 встановимо табличне значення

2

^0,05 =7,815.

9. Порівняємо фактичне значення %2, розраховане за даними вибірки, з табличним:

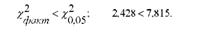
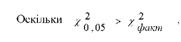
нульова гіпотеза про нормальний розподіл господарств за надоями молока на корову приймається. Іншими словами, фактичні дані узгоджуються з нульовою гіпотезою.