Теорія статистики - Мармоза А.Т. - 8.4. Дисперсійний аналіз при групуванні даних за двома ознаками

В статистичній практиці частіше мають справу з багатофакторними дослідами, в яких вивчають вплив на результативну ознаку двох і більше факторів одночасно.

За аналогією з комбінаційними групуваннями багатофакторні моделі дисперсійного аналізу мають незаперечну перевагу порівняно з однофакторними моделями: вони дають змогу виявити ступінь впливу не тільки кожного фактора окремо, а й їхню взаємодію. Наприклад, ефективність добрив підвищується при покращенні догляду за рослинами, переваги високоврожайних сортів повністю проявляються при високій агротехніці їх вирощування. Ці завдання розв'язуються за допомогою побудови комбінаційних групувань і таблиць. Методи ж розкладання варіації дають числові характеристики взаємодії факторів, а використання імовірнісних оцінок дає змогу зробити висновок про її вірогідність.

Дисперсійний аналіз при групуванні даних за двома факторами ведеться за тією самою принциповою схемою, що й при групуванні даних за одним фактором. При цьому також необхідно враховувати порядок формування груп: випадкове чи невипадкове (незалежні чи залежні вибірки). При залежному формуванні вибірок схема розкладання суми квадратів відхилень ускладнюється в зв'язку з виділенням суми квадратів відхилень повторень.

Відмінність багатофакторного аналізу від однофакторного полягає в тому, що загальний обсяг варіації розкладається на більше число компонентів. В міру розкладання сукупності на групи і підгрупи ускладнюються розрахунки з розкладання загального обсягу варіації на складові частини, а також аналіз дисперсій.

Розглянемо схему розкладання загальної варіації на складові частини для випадку з двома факторами (А і В). Джерелами варіації при групуванні даних за двома факторами будуть: перший фактор - А, другий фактор - В, їх взаємодія - АВ, залишкове варіювання.

Тоді загальну суму квадратів відхилень можна подати в такому вигляді: "¥заг = "¥А + "¥в + "¥АВ + "¥зал.

Розкладання загальної варіації доцільно здійснити в два етапи. Для цього потрібно побудувати дві таблиці. На першому етапі із загального варіювання слід виділити варіацію, пов'язану з двома факторами і залишкову варіацію:

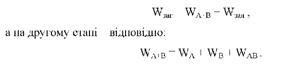
Такий порядок розкладання загальної варіації справедливий для незалежних вибірок. Якщо ж вибірки залежні (наприклад, рендомізовані блоки, латинський квадрат тощо), то з'являється новий компонент варіації, пов'язаний з повторностями

Тоді схема розкладання загальної варіації набуває такого вигляду:

I етап "¥заг = "¥А+В + "¥повт + "¥зал ;

II етап "¥А+В = "¥А + "¥в + "¥АВ ;

і в цілому Шзяг = "¥А + "¥в + "¥АВ + "¥повт + "¥зал.

Для випадку з трьома факторами і залежними вибірками схема розкладення загальної варіації ускладнюється:

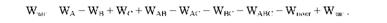
Факторні моделі з великою кількістю факторів (трьома і більше) доцільно досліджувати кореляційним методом з використанням ЕОМ.

Використання дисперсійного аналізу при групуванні даних за двома факторами розглянемо на такому прикладі. В польовому досліді вивчався вплив різних доз добрив на урожайність озимої пшениці, висіяної на ділянках з різними попередниками (табл. 8.5).

Таблиця 8.5. Урожайність озимої пшениці, ц/га

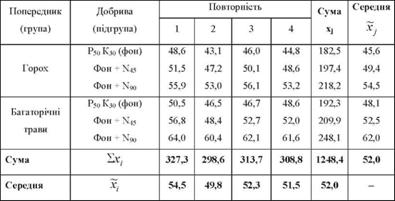
Схема побудови досліду така: ділянку, на якій проводився дослід, було розбито на чотири блоки, що відрізняються між собою рельєфом і механічним складом ґрунтів. Кожен з варіантів досліду у випадковому порядку було розподілено в усіх чотирьох блоках, чим зумовлювалося значне вирівнювання умов в усіх перевірюваних варіантах досліду. Отже, дослід проведено в чотирьохкратній повторності і побудовано за методом рендомізованих блоків (залежні вибірки).

Потрібно методом дисперсійного аналізу перевірити статистичну гіпотезу відносно середніх у генеральних сукупностях.

Порівнюючи середню урожайність по групах (попередниках) і підгрупах (добривах), можна помітити, що урожайність озимої пшениці закономірно зростає по мірі зміни попередника і збільшення доз добрив. Разом з тим висунемо нульові гіпотези про випадковість відмінностей середньої урожайності за варіантами досліду, тобто про те, що фактори не впливають на рівень урожайності озимої пшениці:

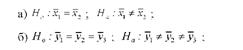
в) Н0: ефективність взаємодії факторів у генеральних сукупностях однакова;

На: ефективність взаємодії факторів у генеральних сукупностях неоднакова;

Тут хі - середні по групах; Х] - середні по підгрупах.

Рівень значущості візьмемо таким, що дорівнює а = 0,05. Для перевірки Но використаємо критерій Б.

Схема побудови досліду показує, що загальну варіацію урожайності озимої пшениці можна розкласти на 5 компонентів:

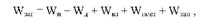
де "¥заг - варіація урожайності за рахунок впливу: попередників ¥п, добрив ¥д, взаємодії факторів (попередників і добрив) "¥вз, повторностей "¥повт; "¥зал - залишкова варіація.

Розкладання загальної варіації проведемо в два етапи. На першому етапі виділимо із загальної варіації

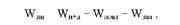
тобто варіацію, що створюється спільним впливом попередників і добрив, варіацію по блоках (повторностях) і залишкову (відхилення індивідуальних спостережень від середніх по кожному фактору окремо).

На другому етапі виділимо варіацію (суму квадратів відхилень), пов'язану з дією факторів (кожного окремо і їхню спільну взаємодію):

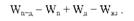
Позначимо число спостережень в досліді N = 24, кількість груп за попередниками т = 2, кількість підгруп за добривами І = 3 і за блоками п = 4 N = тІп = 2 o 3 o 4 = 24).

Для спрощення обчислень сум квадратів відхилень зменшимо всі вихідні дані на постійну величину, близьку до середньої величини (а = 50) і виразимо дані досліду у відхиленнях від постійної величини.

Результати обчислень запишемо в табл. 8.6.

Таблиця 8.6. Відхилення від умовного початку (у = х - а; а = 50)

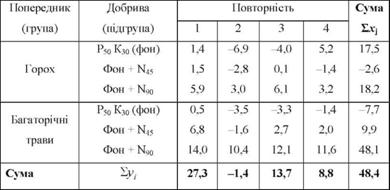
Перевіримо правильність розрахунків: загальна сума урожайності (іх,7 = 1248,4) має дорівнювати сумі відхилень від умовного початку = 48,4), плюс добуток умовного початку на кількість спостережень (атУ):

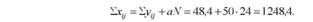
Для визначення сум квадратів відхилень "¥заг; "¥п+д; "¥повт і Wзaл піднесемо до квадрата всі індивідуальні відхилення, їх суми по графі і рядку і

загальний підсумок (табл. 8.7).

Таблиця 8.7. Квадрати відхилень

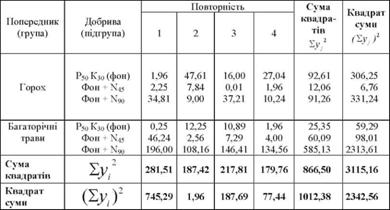
В результаті піднесення до квадрата відхилень отримаємо всі потрібні дані для визначення сум квадратів відхилень на першому етапі:

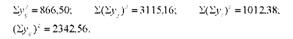
Користуючись одержаними сумами, визначимо необхідні суми квадратів відхилень:

Для кожної суми квадратів відхилень визначимо число ступенів свободи варіації:

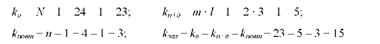
На другому етапі проведемо розкладання варіації, пов'язаної з дією факторів (за рахунок кожного фактора та їх взаємодії):

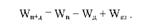
Для розрахунку необхідних сум квадратів відхилень на підставі даних останнього стовпця табл. 8.6 складемо нову таблицю відхилень (табл. 8.8), в якій назви рядків містять градації за попередниками, а стовпців - за дозами добрив. Позначимо суми відхилень за попередниками - А, а за дозами добрив - В і піднесемо до квадрата відхилення (табл. 8.9).

Таблиця 8.8. Відхилення по варіантах досліду

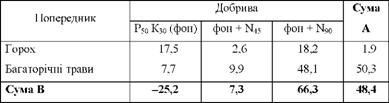
Таблиця 8.9. Квадрати відхилень по варіантах досліду

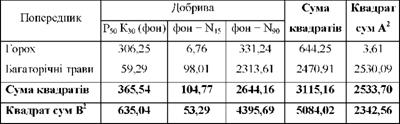
Сума квадратів відхилень в табл. 8.9. (3115,16) дорівнює підсумку останньої графи табл. 8.7. На підставі цієї суми було визначено варіацію урожайності, зумовленої спільною дією двох факторів:

"¥п+д = 681,18 з числом ступенів свободи кп+д = 5.

Ця сума квадратів відхилень складається із таких складових компонентів:

Визначимо число ступенів свободи варіації для кожної з обчислених сум квадратів відхилень. Для цього необхідно ступені свободи варіації двох факторів (кп+д = 5) розподілити між трьома компонентами, що складають цю суму квадратів відхилень (кп , кд і кю):

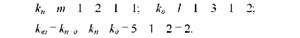
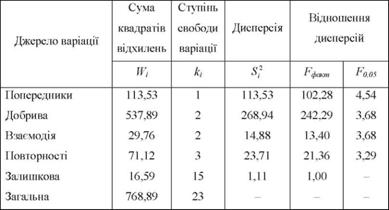
Об'єднаємо результати обчислень двох етапів, розрахуємо і проаналізуємо дисперсії (табл. 8.10).

Таблиця 8.10. Розрахунок і аналіз дисперсій

Фактичне дисперсійне відношення знайдемо за формулою

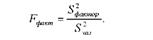
о2 . п2

Наприклад, по добривах становитиме д o = 268,94 : 1,11 =

242,29, по взаємодії факторів евз : езад = 14,88 : 1,11= 13,40 і т.д. Табличні значення Б при рівні значущості а = 0,05 визначимо за додатком 4 для оцінки відношення дисперсії попередників до дисперсії залишкової - на перетині 1-го стовпця і 15-го рядка (Б005 =4,54); для відношення дисперсії добрив до дисперсії залишкової - 2-го стовпця і 15-го рядка (Б005 = 3,68) і т.д.

Порівняння фактичних і табличних значень Б-критерію Фішера при заданому рівні значущості а = 0,05 показує, що в усіх випадках Тфщт > Б005.

Отже, висунуті нульові гіпотези не узгоджуються з фактичними даними і тому їх потрібно відхилити. Відмінності в урожайності за факторами і повторностями є істотними, вірогідними, вірогідним є проявлення ефекту взаємодії факторів.

Оскільки за результатами дисперсійного аналізу нульові гіпотези відхилено і доведено істотність відмінностей між середніми, можна оцінити вірогідність різниць між парами середніх. Для цього потрібно обчислити середню і можливу граничну помилку вибірок (Єр) і аналогічно тому, як це було зроблено в попередньому прикладі, знайти фактичні різниці між парами середніх і порівняти їх з можливими граничними різницями (НІР).