Найпростішим видом кореляційного зв'язку є зв'язок між двома ознаками: результативною і факторною. Такий зв'язок називають парною кореляцією або простою кореляцією.
В економічних дослідженнях взаємозв'язку двох факторів серед множини функцій часто розглядається прямолінійна форма зв'язку, яка виражається рівнянням прямої лінії
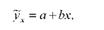
де Ух - вирівняне значення результативної ознаки (залежна змінна); х -значення факторної ознаки (незалежна змінна); а - початок відліку, або значення Ух при Ь = 0 (економічного змісту не має); Ь - коефіцієнт регресії, який показує середню змінну залежної змінної при зміні незалежної змінної на одиницю (одне своє значення).
Коефіцієнти регресії є величинами іменованими і мають одиниці вимірювання, що відповідають змінним, між якими вони характеризують зв'язок.
Якщо Ь > 0, то зв'язок прямий, якщо Ь < 0, то зв'язок обернений, якщо Ь = 0, то зв'язок відсутній.
Параметри рівняння а і Ь визначають способом найменших квадратів. Він дає можливість знайти ту криву, яка порівняно з іншими кривими проходить найближче до точок кореляційного поля, що відображають фактичні дані, тобто дає найменшу суму квадратів відхилень фактичних значень результативної ознаки від вирівняних (теоретичних) значень:
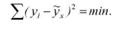
Порядок одержання системи нормальних рівнянь при парній кореляції такий. Для одержання першого рівняння системи необхідно всі члени вихідного рівняння кореляційного зв'язку помножити на коефіцієнти при першому невідомому (а) і одержані добутки підсумувати. Потім для отримання другого рівняння необхідно всі члени вихідного рівняння помножити на коефіцієнт при другому невідомому (Ь) і також всі добутки підсумувати.
Техніка одержання системи нормальних рівнянь залишається аналогічною і для побудови системи рівнянь з більшим числом змінних. Так, для парного лінійного зв'язку система нормальних рівнянь має вигляд:
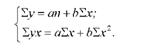
Параметри а і Ь рівняння прямої лінії можна визначити за іншими робочими формулами :
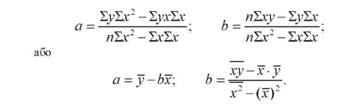
Рівняння кореляційного зв'язку мають як пізнавальне, так і практичне значення, їх використовують для обчислення теоретичної лінії регресії, очікуваних (теоретичних, вирівняних) і прогнозованих значень залежної змінної при тих або інших значеннях фактора (факторів). При цьому слід мати на увазі, що рівняння дає середнє співвідношення між результативною і факторною ознаками, тому найбільшу точність збігання мають розрахункові значення результативної ознаки при величині фактора, близького до середнього його рівня.
Ступінь наближення розрахункових значень результативної ознаки до її фактичного значення залежить від того, наскільки досконала кореляційна модель. Якщо вона включає всі основні фактори, що визначають варіацію результативної ознаки, то точність буде досить високою.
Розглянемо приклад аналізу кореляційного зв'язку між двома ознаками (парна кореляція): продуктивністю корів - надоєм молока на середньорічну корову (ц) і рівнем годівлі - витратами кормів на одну корову за рік (ц кормових одиниць; табл. 9.1).
Таблиця 9.1. Розрахунок даних для визначення показників кореляційного зв'язку
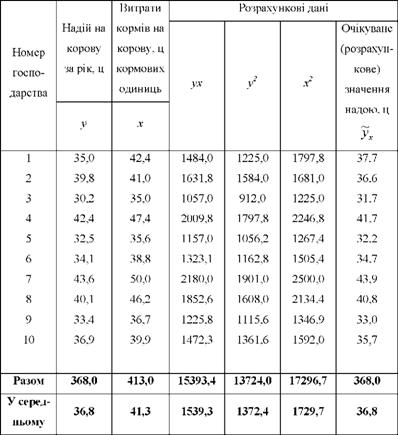
Результативною ознакою в даному прикладі є продуктивність корів (у), а факторною - рівень годівлі (х).
Для визначення форми зв'язку між продуктивністю корів і рівнем годівлі побудуємо графік - кореляційне поле (рис. 9.1.). На осі абсцис відкладемо значення факторної ознаки (незалежної змінної - рівня годівлі, а на осі ординат - результативної ознаки (залежної змінної - продуктивності корів).
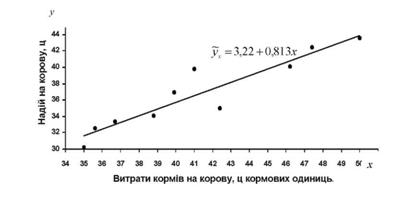
Рис. 9.1. Кореляційне поле залежності надою на корову від витрат кормів
Графік показує, що в даному випадку зв'язок близький до прямолінійного і його можна виразити рівнянням прямої лінії
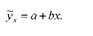
Розв'язання цього рівняння регресії покаже зміну продуктивності корів під впливом рівня годівлі при виключенні випадкових коливань ознаки.
Параметри рівняння прямої лінії а і Ь знайдемо із системи нормальних рівнянь:
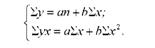
Усі необхідні для розв'язання системи рівнянь дані розрахуємо в табл. 9.1. Одержані дані підставимо в систему рівнянь:
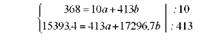
Поділимо рівняння на коефіцієнти при а, тобто перше рівняння на 10, а друге - на 413:
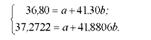
Віднімемо перше рівняння із другого:
0,4722 = 0,5806 Ь , звідси Ь = 0,4722 : 0,5806 = 0,813 ц на 1 ц кормових одиниць. Підставимо значення Ь = 0,813 в перше рівняння і знайдемо а:
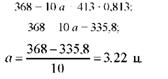
Рівняння регресії (кореляційне рівняння), яке виражає зв'язок між продуктивністю корів і рівнем годівлі буде мати вигляд:
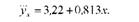
Коефіцієнт регресії Ь = 0,813 показує, що з підвищенням рівня годівлі на 1 ц кормових одиниць продуктивність корів в середньому по даній сукупності господарств зростає на 0,813 ц.
Параметри рівняння регресії можна визначити і за іншими формулами:

Перевіримо правильність розв'язання системи рівнянь, виходячи із рівності
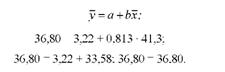
За рівнянням регресії можна розрахувати очікувані (розрахункові або теоретичні) значення продуктивності корів (ух) при різних значеннях витрат кормів на корову (*). Для цього замість х підставимо його конкретні значення:
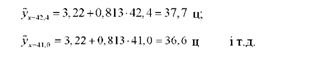
Усі обчислені дані запишемо в останню графу таблиці 9.1. За цими даними на рис. 9.1 побудуємо теоретичну лінію регресії.
Перевіримо правильність усіх розрахунків зіставивши суми фактичного і розрахункового надою молока на корову:
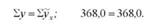
9.4. Криволінійна кореляція
9.5. Статистична оцінка вибіркових показників зв'язку
9.6. Непараметричні критерії оцінки кореляційного зв'язку
9.7. Особливості кореляційного аналізу в рядах динаміки
Розділ 10. Ряди динаміки
10.1. Поняття про ряди динаміки і їх види. Наукові умови побудови рядів динаміки
10.2. Показники ряду динаміки
10.3. Прийоми виявлення основної тенденції розвитку в рядах динаміки
10.4. Факторний аналіз рядів динаміки