Математична статистика - Руденко В.М. - Метод моментів

За цим методом (запропоновано К. Пірсоном) певна кількість вибіркових моментів (початкових v_k або центральних m_k, або тих і інших) прирівнюють до відповідних теоретичних моментів ( ~_k або щ ) розподілу випадкової величини X. Нагадаємо, що вибіркові моменти визначаються за формулами (2.13 - 2.20 ), а відповідні теоретичні моменти - за формулами (3.14 - 3.39). Отже, оцінки невідомих параметрів є рішенням системи рівнянь. Кількість рівнянь визначається кількістю параметрів, що підлягають оцінюванню.

Приклад 4.1. Визначити точкові оцінки випадкової величини X, що має нормальний розподіл, за методом моментів.

Рішення:

Щільність нормального розподілу випадкової величини X має вигляд

f (x; fi,a ) = exp<!--- з двома невідомими параметрами: серед-

л/2я-сг² І ²° J

нім іл = M[X] = v₁ (3.36) і дисперсією о² = D[X] = m₂ (3.37), які є першим

початковим і другим центральним теоретичними моментами.

Відповідні вибіркові моменти мають вигляд: ^v1 = ^- Е^xi і m₂ = v₂ - v_x² .

ⁿ і=1

Звідси визначається система з двох рівнянь:

1 "

ﳥ1

Рішення системи рівнянь дає оцінки середнього ju_MM і дисперсії сг_мм за методом моментів

Ь ⁼ 2 (4.7)

<т = з

Як бачимо, точковими оцінками середнього і дисперсії випадкової величини x, що має нормальний розподіл, є вибіркові середнє X і дисперсія з².

Оцінювання за методом моментів є спроможним, порівняно простим у розрахунках, але за показником ефективності не "найкращим". Основним методом отримання оцінок параметрів генеральної сукупності вважається метод максимальної правдоподібності, запропонований Р.Фішером.

Метод максимальної правдоподібності

Основу метода складає функція правдоподібності Ь(х; ©) , яка виражає ймовірність спільної появи результатів вибірки х_ь х₂, х_п:

ц х1, х2, - , Хп ;®) = ф( Х1,@) -ф( Х₂,&) ■■■■?( Хп , ©).

Згідно з метод максимальної правдоподібності за оцінку невідомого параметра © приймається таке значення ®_п, яке максимізує функцію ц( х;0) ²⁰.

Приклад 4.2. Визначити точкові оцінки параметрів випадкової величини x, що має нормальний розподіл, за методом максимальної правдоподібності. Рішення:

Щільність нормального розподілу випадкової величини x визначається

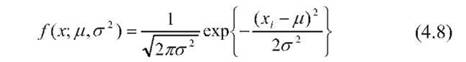
і має два параметри: середнє ц і дисперсію а², які слід оцінити. Функція правдоподібності має вигляд

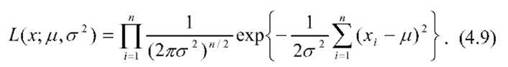
Після логарифмування потримаємо

²⁰ Див., наприклад, Н.Кремер [41, С. 303-305].

ТІ 1 п

1пЬ = --(1па² +111(2*)) - -- X(х_і - /и)². (4.10) ² 2сг ,=1

Для знаходження параметрів ц і а² часткові похідні за цими параметрами

необхідно прирівняти нулю і розв'язати відповідну систему рівнянь:

--= - їй ^(хі = ⁰

'а іп ь 1 л _{( )}2 п ₀ ^(4.11)

З першого рівняння (для (7²>0) отримаємо

п п п п 1 ^п ,

X^(х, ⁼ Е^х, = Е^х, "^п<"⁼⁰, звідки М = -2^^х, , тобто

¿=1 ¿=1 ¿=1 ¿=1 ^п і=1

ї ™ = (4.12)

З другого рівняння після скорочення (для о²>0) і підстановки отримаємо

-X (х, - X)² - п = 0, звідки ^а2=~2І^(х, ~ ^Х)2 , тобто

= ^ (4.13)

Таким чином, оцінками за методом максимальної правдоподібності математичного сподівання /й_ямп і дисперсії випадкової величини x, що має

нормальний розподіл, є відповідно вибіркове середнє x і вибіркова дисперсія ^² . Оцінки за методом моментів і методом максимальної правдоподібності для середнього і дисперсії співпадають, але тільки для випадкової величини x, що має нормальний розподіл.

Оцінки максимальної правдоподібності, як правило, є спроможними і асимптотично ефективними. Основний недолік цього методу пов'язаний з труднощами розрахунку оцінок, а також і те, що для побудови оцінок і забезпечення їх "найкращими" властивостями необхідно знати закон розподілу випадкової величини, що у багатьох випадках виявляється практично нереальним.