При зоровому сприйнятті показників рядів розподілу і їх графіків переконуємося, що розмір варіант має деякі загальні закономірності, які проявляються в тому, що їх величини групуються навколо центра розподілу. За даними статистичного ряду при віддаленні від центра розподілу вгору і донизу, а при графічному зображенні при віддаленні вправо і вліво частоти постійно спадають.
Тенденція значень ознаки групуватися навколо центра розподілу частот, статистичною характеристикою якого є середня арифметична
(х), називається центральною тенденцією.
Таким чином, виникає необхідність розрахунку характеристик статистичних рядів розподілу.
Найважливішою характеристикою варіаційного ряду розподілу є середня величина. Статистичні середні відображують об'єктивну наявність певних умов, які проявляються в кожній одиниці досліджуваної сукупності; вони дають узагальнюючу кількісну характеристику статистичним сукупностям однотипних явищ по варіаційній ознаці. Середня узагальнює або являє собою весь діапазон даних і є результатом абстрагування відмінностей, що притаманні одиницям сукупності. В ній нівелюються випадкові відхилення, властиві індивідуальним значенням ознаки, яка вивчається, а також відображаються загальні умови, що формують досліджувану сукупність.
Середні величини можуть бути одержані в результаті багаторазових вимірювань однієї й тієї ж ознаки (величини). Середні одержують і при вимірюванні багатьох однорідних величин.
Розрахунок середніх передбачає обов'язковість обліку умов виникнення кожної індивідуальної величини, інакше обчислення можуть призвести до фіктивних середніх. Щоб середня величина відбражувала типове і загальне для всієї сукупності, остання повинна бути якісно однорідною.
Статистика розрізняє два типи середніх величин: об'ємні і структурні. Математична статистика поділяє об'ємні середні величини на види: 1) середня арифметична; 2) середня геометрична; 3) середня гармонійна; 4) середня квадратична (кубічна) і т.д.
Названі вище види середніх величин можна одержати з формули степеневої середньої. Для незгрупованих даних формула степеневої
- і І,х"
середньої має вигляд: ' п
Якщо дані згруповані і мають відповідні частоти (п), середня степенева визначається за формулою середньої зваженої:
- |іх*п, х = її- ,
де х - степенева середня;
к - показник степеня, що визначає вид середньої;
х - варіанта;
п - частота (п = І/П> ).
Середня арифметична. Якщо в формулу степеневої середньої поставити значення к = 1, отримаємо середню арифметичну:
а) просту (незважену) п
- Бх-
б) зважену І,п> .
Так, якщо є х1х2х3, хп ,то середня арифметична проста вираховується за формулою:
- X + Х2 + Х3 + ... + X X = -1-2-3--.
п
У розгорнутому вигляді формула середньої арифметичної
- х1п1 + х п2 + х3п3 +... + хппп
X =-2-.
зваженої має вигляд: п + п2 + -3 +... + пп
Приклад. За даними про виробництво валової продукції обчислити середню арифметичну. Дані берем з таблиці 10.
Таблиця 10
Вихідні і розрахункові дані
Вироблено продукції, МЛН.ГрН., ( Хі) | Кількість підприємств (п;) | Хіпі |
17,6 | 7 | 123,2 |
21,6 | 11 | 237,6 |
25,6 | 18 | 460,8 |
29,6 | 9 | 266,4 |
33,6 | 5 | 168,0 |
37,6 | 5 | 188,0 |
41,6 | 2 | 83,2 |
Всього | 57 | 1527,2 |
- Хх,п, 1527,2 268 х = -- =-= 26,8
Одержуємо: 57 .
Середня арифметична як математична функція має ряд математичних властивостей. Розглянемо їх.
1. Величина середньої арифметичної не змінюється, якщо частоти ряду розподілу замінити частостями.
2. Якщо до варіант ряду додати (або відняти) одну й ту ж величину, то середня арифметична, обчислена з нових (змінених) варіант, збільшиться (або зменшиться) на цю ж величину.
3. Якщо варіанти ряду помножити або поділити на одну ту ж величину, то середня арифметична зі змінених варіант буде відповідно більшою або меншою в стільки ж разів.
4. Алгебраїчна сума відхилень окремих варіант від середньої арифметичної ряду дорівнює нулю.
5. Сума квадратів відхилень від середньої арифметичної завжди менша, ніж сума квадратів відхилень від будь-якої іншої величини.
Перелічені вище властивості середньої арифметичної дозволяють застосовувати спрощені прийоми (способи) її розрахунку: ці питання докладно вивчаються в курсі загальної теорії статистики.
Середня гармонійна. Одержують її при підстановці у формулу степеневої середньої значення к = - 1.
- І І,х~1 1 п
Хгм " п 11 11
X X .
Середня гармонійна зважена має вигляд:
- Еи<
х
Як видно, середня гармонійна являє собою обернену величину середньої арифметичної з обернених величин даних чисел.
Приклад. За даними про собівартість одиниці продукції і загальні витрати визначити середню гармонійну зважену (табл. 11).
Таблиця 11
_Вихідні і ^ розрахункові дані__
Собівартість одиниці продукції, | Загальні витрати, грн. | № |
грн. (х,) | X | |
20 | 4000 | 200 |
25 | 5000 | 200 |
30 | 9000 | 300 |
x | ^ =18000 | * =700 |
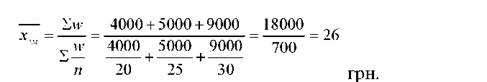
При розрахунку середньої гармонійної можна значно спростити обчислювальну роботу, якщо використовувати в розрахунках таблицю обернених чисел.
Середня геометрична. Цей вид середньої отримуємо, якщо у формулу степеневої середньої підставити значення к = 0.
-х="ІН=0р= (* )0 = ґ- Т = 1"
V п V п п п)
Розкриття невизначеності цього виду досягається логарифмуванням обох частин рівностей ' п .Таким чином, маємо:
- 1 к 1п їх" - 1п п
1п х = - (1п їх - 1п и) =-
к п .
Диференціюючи по змінній к, одержуємо:
1іт (1п х) = Ііт ^х х 111 х 1п х . - 11п х - 1хІх* п 1п х = --
Потенціюючи останній вираз, знаходимо середню:
Отже, середня геометрична являє собою корінь степеня числа спостережень (п) з добутку даних чисел : хьх^ х3, . ", хп. Після логарифмування маємо:
1 - _ ІЕх + 1gх2 + ^х3 +... + ^х-1§ х
п.
Значення х дорівнює антилогарифму 1е х.
Таким чином, середню геометричну можна розглядати як антилогарифм середньої арифметичної з логарифмів даних чисел. Цей вид середньої застосовують при розрахунку середнього коефіцієнта зростання за певний період в рядах динаміки.
Приклад. За даними про чисельність працюючих за 6 років знайти середній щорічний коефіцієнт зростання за період 1997-2002 рр. Проміжні розрахунки наведені в таблиці 12.
Таблиця 12
Вихідні дані і розрахунки для обчислення середньої геометричної | |||
Рік | Чисельність працюючих | Коефіцієнт зростання, к | Логарифм числового значення коефіцієнта зростання |
1997 | - | - | |
1998 | 670 | 1,07545 | 0.0315 |
1999 | 728 | 1.08657 | 0,0363 |
2000 | 800 | 1,09891 | 0,0411 |
2001 | 883 | 1,10375 | 0,0429 |
2002 | 906 | 1.02605 | 0,0111 |
Сума | X | X | 0,1629 |
За даними таблиці 12 знаходимо середнє значення з логарифмів числових значень коефіцієнтів зростання: lg к = 0,1629:5 = 0,0326; ant lg0,0326 = 1,077
Таким чином, розрахунок середнього коефіцієнта зростання чисельності працюючих можна подати в такій послідовності:
lg К5/1,075 х 1,087 х 1,099 х 1,104 х 1,026 = 0,0315 + 0,0363 + 0,0411 + 0,0429 + 0,0111 = 0,0326 _ К = ant lg0,0326 = 1,077
Середня квадратична. При підстановці у формулу степеневої середньої k = +2 одержуємо середню квадратичну. Формула її має наступний вигляд:
- _ iLx1 _ Ixf + x + x32 +... + xl при незваженій формі - " V n V n ;
при зваженій формі -
- YLx2ni x^nt + x2n2 + x32n3 +... + x^nn "° у ~Lnt у n + n2 + n3 +... + nn
Практично середня квадратична величина використовується в тих випадках, коли варіанти ряду представлені у вигляді відхилень фактичних їх значень від середньої арифметичної (або від якоїсь нормативної величини).
Приклад. При змінній нормі виробітку трактора на оранці 7 га обчислити середню величину відхилень фактичних показників виробітку протягом робочого тижня (табл. 13).
Таблиця 13
Вихі/іні та по'ш;і\іік'ош лані /іля обчислення cene/іньоїігаа/іііатичної
Фактичні показники виробітку трактора, га (хі) | Відхилення від норми, га (х,-хн)=М | Кількість тракторів, Пі | Розрахункові величини | |
М 2 | М 2 n | |||
6 | -І | 1 | 1 | 1 |
7 | 0 | 5 | 0 | 0 |
8 | 1 | 6 | 1 | 6 |
10 | 3 | 3 | 9 | 27 |
12 | 5 | 6 | 25 | 150 |
Всього | X | 21 | x | 184 |
За даними таблиці 13 знаходимо величину середньої квадратичної
- І їх,2 - ІЇ84 г- ""^
х = -- = ,-= л/8,76 ~ 2,96
.. "в V Іп. V 21 зваженої ' ' .
Отже середня величина відхилень фактичних показників виробітку
трактора на оранці від норми виробітку становить приблизно 3 га (2,96).
Формули для обчислення різних типів середніх величин наведено в таблиці 14.
Ознаки, які вивчаються, можуть бути первинними і вторинними. До первинних відносяться ті, які безпосередньо характеризують досліджувані об'єкти, наприклад, урожайність, собівартість тощо. Відношення двох чи декількох первинних ознак обумовлює характер вторинності - їх називають вторинними. За формою ознаки можуть бути прямі і обернені. Названі особливості досліджуваних ознак визначають статистичну розмірність (табл. 14).
Таблиця 14
Математичні особливості різних типів середніх величин_
Характер ознаки | Форма величини (ознаки) | Статистична розмірність (показник степеня в формулі степеневої середньої) | Вид середньої величини | Форма середньої величини | Формула |
Первинний | Обернена | -1 | Гармонійна | Проста | - п "■ Ті X |
Вторинний | Обернена | -1 | Гармонійна | Зважена | - їй" X |
Вторинний | Пряма | 0 | Геометрична | Проста | X2^ - д^-^і X --^2 X Х3 ... X ЭС^ |
Первинний | Пряма | 1 | Арифметична | Проста | - їх п |
Вторинний | Пряма | 1 | Арифмет ична | Зважена | - Ъх1п1 Х" ~ Ъщ |
Первинний | Пряма | 2 | Квадрати чна | Проста | - їх1 V п |
Вторинний | Пряма | 2 | Квадрати чна | Зважена | - їх2 п "в Іп, |
Різні види середніх, розраховані для одного і того ж варіаційного ряду, різняться між собою за величиною. При цьому найменшою буде середня гармонійна, найбільшою - середня квадратична. Систематичність послідовного зростання у розрізі видів середніх випливає з "правила мажорантності" і зумовлюється показником у формулі степеневої середньої (табл. 15).
Таблиця 15
Мажорантність середніх величин _
Статистична розмірність (показник степеня в формулі степеневої середньої) | Вид середньої величини | Примітка |
-1 | Гармонійна | Мінімальна |
0 | Геометрична | |
1 | Арифметична | |
2 | Квадратична | Максимальна |
Хг* < Хгр < Ха і Хт | ||
У дискретному і інтервальному рядах розподілу обчислюються так названі порядкові (структурні) середні - мода і медіана.
Мода - це варіанта, яка найчастіше зустрічається в даному варіаційному ряді. Для дискретного ряду розподілу мода визначається за частотами варіант і відповідає варіанті з найбільшою частотою. Для інтервального ряду розподілу з рівними інтервалами інтервал, що містить моду (модальний), визначається по найбільшій частоті. При нерівних інтервалах мода знаходиться за показником найбільшої щільності розподілу.
Для випадку розподілу з рівними інтервалами мода (Мо) внутрімодального інтервалу обчислюється за формулою:
М 0 = хт шіл +1-----,
(п*о " пш-і) + (п"о " п"о+і)
де х"оші" - нижня границя модального інтервалу; і- інтервальна різниця (величина інтервалу); п*°- частота модального інтервалу; ""о-1- частота інтервалу, що передує модальному; п"°+1 частота інтервалу, наступного за модальним.
Медіана - це значення варіаційної ознаки, яка приходиться на середину варіаційного ряду. Якщо кількість членів ряду парна, то медіана дорівнює середній арифметичній із двох серединних значень варіант.
Для обчислення медіани інтервального варіаційного ряду знаходять інтервал, який містить медіану, шляхом використання нагромаджених частот або частостей. Медіанному інтервалу відповідає перша з нагромаджених частот або частостей, що перевищує половину всього обсягу сукупності. Внутрі знайденого інтервалу медіана (Ме) розраховується за формулою:
Ме = хте тіп + і --
де хметіп - нижня границя медіанного інтервалу; і -
. . . 1 ^пі
інтервальна різниця (величина інтервалу); 2 - половина суми
всіх частот або частостей; 8ме-1 - нагромаджена частота або частость інтервалу, який передує медіанному; пме - частота медіанного інтервалу.
Карл Пірсон встановив взаємозв'язок між модою, медіаною і середньою арифметичною, який виражається рівністю:
1 2-
М" = -М0 + - Ха.
3 0 3
Приклад. За даними інтервального ряду розподілу підприємств по врожайності зернових культур знайти середній показник урожайності, використовуючи у розрахунку формули структурних середніх - моди і медіани.
Таблиця 16
Вихідні і розрахункові дані_
Урожайність, ц з I га (хі) | Кількість підприємств, частота ( пі.) | Нагромаджена сума частот ( п'і) |
16-20 | 3 | 3 |
20-24 | 6 | 9 |
24-28 | 17 | 26 |
28-32 | 16 | 42 |
32-36 | 7 | 49 |
36-40 | 5 | 54 |
40-44 | 3 | 57 |
Всього | 57 | х |
У складеному інтервальному варіаційному ряді (табл.16) модальним інтервалом, із найбільшим числом варіант (17), є третій інтервал з рівнем урожайності від 24 до 28 ц. Отже, мода повинна знаходитися всередині цього інтервалу. Підставивши в наведену вище формулу необхідні значення, одержимо:
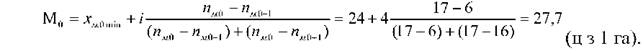
Обчислимо медіану за даними цього ж інтервального ряду розподілу. Як уже було сказано, медіана (Ме) в статистичному ряді розподілу посідає центральне місце. Для її знаходження необхідно мати нагромаджений підсумок частот. Медіана знаходиться в тому інтервалі, нагромаджена сума частот якого дорівнює або більша за напівсуму частот ряду (57 : 2). У розглянутому прикладі таким інтервалом є четвертий, з рівнем урожайності від 28 до 32 ц, оскільки тут нагромаджена сума частот становить 42. Підставивши відповідні значення у формулу медіани (Ме) одержимо:
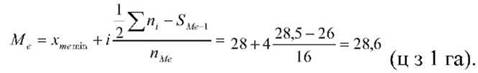
ТЕМА 5. АНАЛІЗ РЯДІВ РОЗПОДІЛУ
§ 5.1. Поняття про статистичні ряди розподілу
§ 5.2. Графічне зображення рядів розподілу. Основні форми статистичних розподілів
§ 5.3. Варіація ознак. Показники варіації
5.3.1. Найважливіші математичні властивості дисперсії
5.3.2. Загальна, міжгрупова і внутрішньогрупова дисперсія
5.3.3. Дисперсія альтернативних ознак
§ 5.4. Моменти статистичного розподілу
§ 5.5. Характеристика асиметрії і ексцесу