Статистика - Опря А.Т. - 7.2.1. Загальнотеоретичні основи кореляційно-регресійного методу аналізу

7.2.1. Загальнотеоретичні основи кореляційно-регресійного методу аналізу

Будь - яке явище природи і суспільства не може бути усвідомленим і зрозумілим без обґрунтування його зв'язків з іншими явищами. Щоб пізнати сутність явищ, необхідно розкрити їх взаємовідносини, кількісно визначити вплив тих або інших об'єктивних і суб'єктивних факторів.

Вплив цих факторів на рівень економічних показників в сільському господарстві до недавнього часу визначався в основному за допомогою методу статистичних групувань (цей метод буде розглянуто в темах загальної теорії статистики). Співвідношення ознак, виявлених в результаті статистичних групувань, відрізняються від співвідношень, які мають місце при функціональних зв'язках, коли кожному значенню аргумента відповідає визначене значення функції. Метод статистичних групувань дозволяє встановити тільки наявність зв'язку між явищами, не визначаючи при цьому його порівняльні кількісні параметри. Через це поряд з методом групувань, які відіграють винятково важливу роль у економічних дослідженнях, для рішення подібних питань необхідно застосовувати і інші методи, зокрема, метод кореляції. Термін "кореляція" вперше застосував Ж.Кюв'є в праці "Лекции по сравнительной анатомии" ( 1800-1805 pp.). Початкові математичні побудови методу кореляції були дані О.Браве у 1846 р. ( "кореляція" - від латинського "correlation" відношення, що означає співвідношення, відповідність предметів або понять).

Кореляцією називається неповний зв'язок між досліджуваними явищами. Це така залежність, коли будь - якому значенню однієї змінної величини може відповідати декілька різноманітних значень іншої змінної. Вона відображає закон множини причин і наслідків і є вільною неповною залежністю.

У дослідженнях важливо вивчати не стільки міру кореляції, скільки форму її і характер зміни однієї ознаки в залежності від зміни другої. Ці задачі розв'язуються методами регресійного аналізу. Перші спроби застосування цього методу в економіці були зроблені у кінці XIX і на початку XX століття ) в Росії - роботи Е.Е.Слуцького, А.А.Чупрова, на Заході - роботи В.Парето, Гукера та ін.).

Кореляційний аналіз є свого роду логічним продовженням (розвитком ) методу статистичних групувань, його поглибленням. Він допомогає вирішити цілий ряд нових завдань у економічному аналізі. Розрахунки на основі кореляційних моделей підвищують ступінь точності аналізу, часто виявляють недоліки попереднього аналізу. Перевага цього методу складається також і в тому, що він дає можливість розв'язувати задачі, які не можна вирішити за допомогою інших методів економічного аналізу - як, наприклад, розділ впливу багатьох факторів, які діють взаємопов'язано і взаємозумовлено.

Використання методу кореляції і регресії дозволяє вирішити такі основні завдання : 1) встановити характер і тісноту зв'язку між досліджуваними явищами; 2) визначити і кількісно виміряти ступінь впливу окремих факторів і їх комплексу на рівень досліджуваного явища; 3) на підставі фактичних даних моделі залежності економічних показників від різних факторів розраховувати кількісні зміни аналізованого явища при прогнозуванні показників і давати об'єктивну оцінку діяльності підприємств.

Відомо, що існує два типи залежності явищ: функціональний і кореляційний. При функціональному зв'язку зміна однієї ознаки чи показника на певну величину викликає за собою зміни другої ознаки чи показника на чітко визначену величину. Такого роду залежність в її чистому вигляді зустрічається в математиці, фізиці, хімії.

При кореляційній залежності будь - якому значенню однієї змінної величини може відповідати декілька чи навіть безліч різноманітних, тобто варіюючих значень іншої змінної величини.

Головна відмінність кореляційної залежності від функціональної полягає в тому, що функціональний зв'язок має місце в кожному окремому випадку спостереження, а кореляційний проявляється так само лише в середньому або в цілому для всієї даної сукупності спостережень і є неточним у відношенні окремих спостережень.

Кореляційний зв'язок величин полягає в тому, що при завданні однії з них встановлюється не одне точне значення, а ймовірності різноманітних значень іншої. Таким чином, залежність виявляється не між самими величинами, а між кожною з них і відповідним математичним очікуванням іншої.

Вивчення взаємозв'язків кореляційного типу має істотне значення особливо при аналізі явищ, які складаються під впливом великої кількості певних умов.

За своїми математичними особливостями кореляційні залежності можуть бути додатними і від'ємними, прямолінійними і криволінійними, простими і множинними.

Коли визначається зв'язок між двома ознаками, кореляція називається простою; якщо ж явище розглядається як результат впливу декількох факторів - множинною. За формою кореляційна залежність буває прямолінійною і криволінійною, за напрямком -прямою ( додатною) і оберненою (від'ємною).

Необхідно підкреслити дві особливості, властиві кореляційному аналізу:

1) при використанні кореляційного методу вирішальне значення має всебічний, економічно усвідомлений попередній аналіз даних господарської діяльності. Слід пам'ятати, що зв'язок між ознаками і властивостями не є результатом математичних розрахунків, а лежить в природі самих економічних явищ і за допомогою методів математичної статистики можна лише виразити об'єктивно існуючі закономірності економічних процесів;

2) кореляцію можна виявити, лише досліджуючи достатньо велику сукупність спостережень, оскільки кореляційні зв'язки виявляються в формі спряженого варіювання двох або кількох зіставлених ознак.

Кореляційно - регресійний аналіз включає три етапи: 1) математико - економічне моделювання ; 2 ) рішення прийнятої моделі шляхом знаходження параметрів кореляційного рівняння (кореляційне рівняння, за первинною пропозицією англійського статистика - математика Ф. Гальтона, називають також рівнянням регресії); 3 ) оцінка і аналіз одержаних результатів.

Статистичне дослідження кореляційної залежності включає завдання визначення форми зв'язку і знаходження кількісної характеристики цієї форми. Процес встановлення форми зв'язку і вибору математичного рівняння, яке могло б найбільш повно відображати характер взаємозв'язку між ознаками досліджуваного явища, має вирішальне значення в кореляційному аналізі.

Питання вибору форми зв'язку та математичного рівняння можна вирішити на основі кількісного соціально - економічного аналізу явищ, що вивчаються, використовуючи при цьому такі методи статистичного аналізу, як графічний, статистичні групування, дисперсійний аналіз та ін .

При прямолінійному зв'язку збільшення факторної ознаки (х) викликає безперечне збільшення (чи зменшення) результативної ознаки (у) у середньому на певну величину.

Повну характеристику лінійного зв'язку можна одержати, користуючись критерієм лінійної кореляційної залежності акад. В.С.Немчинова³. Цей критерій являє таку схему:

1) у^х = у ■^х = повна відсутність лінійного кореляційного зв'язку;

2) у^{х у} у o^х - прямий зв'язок між ознаками;

3) у^х < у ■^х - зворотний зв'язок між ознаками;

4) ух ■ у ■ х = ау -ах - _повна лінійна функціональна залежність.

У випадку, коли в кореляційному аналізі використовують групові середні, характер зв'язку між ознаками визначають за зміною останніх. Більш чи менш правильна систематична зміна їх від групи до групи свідчить про наявність прямолінійної залежності.

Показником тісноти зв'язку є лінійний коефіцієнт кореляції, величина якого визначається за такою формулою:

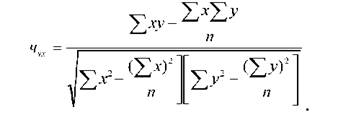
₌ ху - х ■ у

Перетворення цієї формули призводить до вигляду: ^{х у} . Коефіцієнт кореляції коливається в межах від 0 ± 1.