Статистика - Опря А.Т. - ТЕМА 9. АНАЛІЗ ТЕНДЕНЦІЙ РОЗВИТКУ ТА КОЛИВАНЬ

§ 9.1. Прийоми аналітичного вирівнювання рядів динаміки

Ряди динаміки, рівні яких впродовж тривалого часу не змінюються зустрічаються досить рідко. Як правило, рівні ряду з часом змінюються, коливаються. Ці коливання для різних явищ неоднакові і можуть бути зумовлені різними причинами. Серед них: випадкові причини, вплив сезонності, дія будь - яких визначальних факторів.

Маючи справу з показниками ряду динаміки, дослідник завжди намагається виявити головну закономірність розвитку явища в окремі проміжки часу, тобто виявити головну тенденцію в зміні рівнів ряду, звільнену від дії різних випадкових факторів. З цією метою ряди динаміки піддають певній статистичній обробці. Остання може бути елементарно простою і більш складною, із застосуванням математичних методів. Завдання щодо їх використання зводиться до одного: елімінування дії випадкових, другорядних причин, а також встановлення характеру дії основних причин, які визначають динаміку досліджуваних явищ. На цій основі можна передбачити динаміку явищ і в майбутньому , що має аналітичне і практичне значення щодо управління процесами виробництва.

Мета інших прийомів (методів) аналізу рівнів динаміки зводиться до побудови математичних функцій динаміки на підставі ізольованих (дискретних) емпіричних спостережень. їх називають методами вирівнювання статистичних рядів. Така функція динаміки і відповідні їм згладжені криві динаміки дають значно більш узагальнююче і наочне уявлення про досліджувану сукупність чи спостережуване явище, ніж звичний матеріал у вигляді статистичних рядів розподілу. Математичні функції дають змогу глибше вивчити фактори, які впливають на формування статистичної сукупності або на динаміку явища у часі.

Змикання рядів динаміки. Цей прийом обробки рядів динаміки застосовують у випадках, коли досліджувані рівні за одні роки неспівставні з рівнями за інші роки. Неспівставність може бути зумовлена різними причинами: територіальними змінами реорганізаційними факторами переходом до інших одиниць виміру і т.д. у таких випадках здійснюють перерахунок рівнів ряду. Наприклад, є дані про середньорічні надої молочного стада корів в господарствах району, територія якого була зменшена в 2004 році (табл. 58).

Оскільки границі адміністративного району у 2002 році змінилися дані за 2000-2002 рр. виявилися неспівставними з даними за 2002-2004 рр. Щоб побудувати ряд динаміки зівставних показників, приймають за базу порівняння рівень 2000 року, для якого є дані у старих і нових межах району. В результаті одержують ряди відносних величин з однаковою базою порівняння, які можна замінити одним зімкненим рядом динаміки. За даними такого ряду розраховують коефіцієнти (темпи) зростання по відношенню до будь - якого року. Так, середній надій у 2004 році по відношенню до 2000 року збільшився на 37,7 % (109,5 : 79,5 =1,377).

Таблиця 58

_ Зведення рядів динаміки до однієї бази порівняння _

Прийоми виявлення загальної тенденції. Найважливішим завданням аналізу ряду динаміки є виявлення закономірності розвитку явища виявлення загальної тенденції динаміки, а також її характеру, типу .

Під загальною тенденцію динаміки розуміють тенденцію до

зростання, стабільності чи зниження рівня певного явища, а під характером (типом) динаміки розуміють ту чи іншу тенденцію зміни аналітичних показників динаміки: абсолютного приросту, коефіцієнта (темпу) зростання або темпу проросту.

Приклад. Розглянемо показники динаміки врожайності окремих культур у сільськогосподарському підприємстві за 6 років (табл. 59).

Таблиця 59

Динаміка врожайності сільськогосподарських культур у сільськогосподарському підприємстві

__І_" '_І_1^_І_-_І__І___1**1

Тут і далі : * абсолютний приріст; **темп приросту.

Наведені дані свідчать про загальну тенденцію зростання врожайності всіх трьох видів сільськогосподарських культур. Але характер такого зростання неоднаковий. Так, абсолютні прирости урожайності картоплі відносно стабільні, а щодо темпів приросту, то тут спостерігаєся тенденція до деякого зниження. Інший характер динаміки мають показники врожайності цукрових буряків: абсолютні прирости тут щорічно збільшуються, тоді як темпи приросту стабілізуються на рівні 11 - 12 %. Урожайність ярого ячменю зростає прискорено, як в абсолютному так і у відносному виразі.

Таким чином, за даними наведеного прикладу переконуємося, що зростання рівнів ряду динаміки може здійснюватися з неоднаковою інтенсивністю. Отже, завдання аналізу зводиться до того, щоб виявити загальні для всього досліджуваного періоду риси змін.

Серед різноманітних форм характеру динаміки виділяють такі її типи: I-абсолютні прирости спадають; II - абсолютні прирости стабільні; III - темпи зростання стабільні; IV - темпи зростання збільшуються.

Для І типу динаміки характерним є те, що при зростанні рівнів ряду спостерігається зниження абсолютного приросту; II тип динаміки показує, що зростання рівнів ряду супроводжується стабільністю абсолютних приростів і зниженням темпів приросту; III тип означає, що при стабільних темпах зростання абсолютні прирости збільшуються; IV - характеризується інтенсивністю зростання рівнів при систематичному підвищенні темпів зростання.

Таким чином, при постійному зростанні рівнів ряду характеристика динаміки у наведених її типів досить різноманітна , тобто інтенсивність зростання тут неоднакова. Наочно ці типи динаміки ілюструє графік (рис. 22 ).

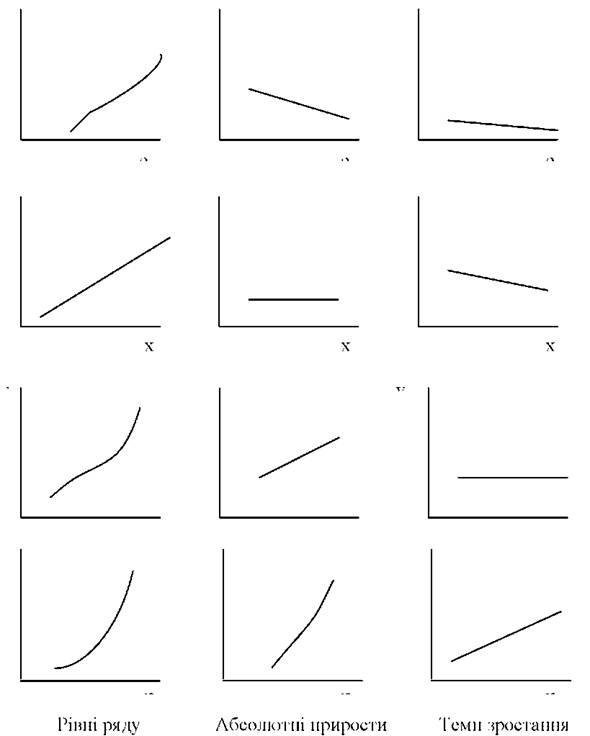
Рис.22. Типи динаміки

Інколи виявити загальну тенденцію розвитку і характер динаміки за ланцюговими показниками не вдається. Це трапляється в тих випадках, коли рівні або одержані ланцюгові показники динаміки значно варіюють, то підвищуючись, то знижуючись. У такому разі основна тенденція розвитку явища ніби затушовується. Щоб її виявити, статистика застосовує такі прийоми: згладжування шляхом укрупнення інтервалів; чи за ковзною (рухомою) середньою.

Згладжування (вирівнювання) шляхом укрупнення інтервалів. Цей найпростіший спосіб виявлення закономірності зміни рівнів динаміки полягає в одержанні середніх або підсумкових показників для укрупнення періодів (інтервалів) часу. Так, наприклад, в рівнях ряду динаміки показників урожайності цукрових буряків по роках спостерігається значна варіація, зумовлена природно - економічними факторами окремих років. Для встановлення тенденції в русі показників урожайності цієї культури розраховують середні значення за трихріччя, п'ятиріччя чи інші періоди.

Згладжування способом ковзної середньої є одним з ефективних методів виявлення загальної тенденції розвитку явища в часі. Суть його полягає в тому, що середній рівень обчислюється спочатку з певного числа перших рівнів ряду, потім - з такої ж кількості рівнів, але починаючи з другого, далі - починаючи з третього і т.д. Розраховані таким чином середні рівні ряду ніби ковзають по ряду динаміки від його початку до кінця, при цьому щоразу відкидається один рівень спочатку і додається наступний. Звідси назва - "ковзна" (рухома) середня. Згладжування таким способом можна здійснювати за будь - яким числом членів ряду. Наприклад, для згладжування ряду динаміки способом ковзної середньої з 5 членів, необхідно послідовно додати 5 членів ряду і результати поділити на 5.

Перш ніж розглянути процес розрахунків ковзних середніх, який проілюстровано таблицею 60, зупинимося на деяких технічних особливостях його здійснення.

Кожна ланка ковзної середньої умовно відноситься (записується чи наноситься на графік) до середини відповідного періоду. При цьому, якщо охоплено парне число рівнів ряду, то середина періоду не збігатиметься з жодним вихідним періодом або датою. У нашому прикладі має місце такий випадок. Одержані ланки ковзної середньої центрують шляхом розрахунку на їх основі двочленних ковзних середніх.

Як бачимо з даних, наведених у таблиці, після згладжування загальна тенденція зростання урожайності зернових культур проявляється досить виразливо. Водночас за такими розрахунками можна більш детально (ніж при звичайному укрупненні інтервалів) прослідкувати і характер динаміки. Так, показники графи 3 таблиці свідчать про те, що зростання здійснювалося нерівномірне і лише центрування згладжує цю нерівномірність.

Таблиця 60

Розрахунок ковзної середньої (6 - річної) динаміки врожайності зернових культур (рівень ряду - в ц з 1 га)

В даному випадку розглянуто приклад згладжування за допомогою 6- річної (6 - членної) ковзної середньої. Питання про кількість років, охоплених ланкою ковзної середньої вирішується в залежності від конкретних особливостей досліджуваного ряду. При цьому, чим довший період, за який обчислюється кожна ланка рухомої середньої, тим сильніше буде згладжено ряд.

Недоліком такого способу вирівнювання є те, що згладжений

п -1

ряд "укорочується" в порівнянні з фактичним на ² члена з початку і кінця ряду динаміки ( п - число членів, з яких розраховується ковзна

Ы = 2,5

середня). У нашому прикладі цей показник становить ² , тобто разом ряд динаміки укорочується на 5 рівнів (2,5 + 2,5), про що свідчить графа 2 таблиці 60.

Отже, одержане число ланок завжди менше вихідних рівнів, а це звужує можливості виявлення характеру (типу) динаміки, оскільки маємо малу кількість аналітичних показників ряду динаміки.

Аналітичне вирівнювання рядів динаміки вважається найбільш удосконаленим способом обробки ряду з метою встановлення тенденції розвитку явища. Завдання такого вирівнювання полягає у знаходженні простої математичної формули (апроксимуючої функції), яка б відображала загальну тенденцію ряда динаміки. Рівні ряду тут розглядаються як функція часу, а завдання (вирівнювання) зводиться до визначення виду функції, її параметрів за емпіричними даними та розрахунку теоретичних рівнів за знайденою формулою.

Суть такого вирівнювання полягає в наступному:

а) на підставі економічного аналізу виділяють певний етап розвитку явища і виявляють характер динаміки протягом цього етапу;

б) виходячи з характеру динаміки обираються той чи інший математичний вираз закономірності, тобто аналітичне рівняння, якому на графіку відповідає певна лінія - пряма, парабола, гіпербола, експонента, логарифмічна крива і т.д.

Підбір емпіричної формули, за допомогою якої здійснюється вирівнювання, відбувається у два етапи : 1) вибір виду функції, яка дає найкраще наближення; 2) визначення параметрів обраної функції.

Як підібрати потрібний вид функції, яка б давала найкраще наближення теоретичної лінії до емпіричних даних? Насамперед слід виходи з економічної суті досліджуваних залежностей і логіко -теоретичних передумов характеру зміни явищ. Зокрема :

1) якщо динаміка характеризується більш чи менш стабільним абсолютним приростом, тобто коли рівні ряду змінюються приблизно у арифметичній прогресії, використовується рівняння прямої лінії

виду ^у>^{= а}°⁺ ^, де ^у< - теоретичний рівень (читається "ігрек", вирівняний по і); 1 - час, ^а° і "1 - параметри прямої;

2) у випадках, коли абсолютні прирости рівномірно збільшується і при згладжуванні крива має один вигин, наближеним математичним виразом цієї тенденції можна обрати параболу другого

порядку : у- = ^а0 + ^а- + °2*²;

3) якщо криві при згладжуванні мають Б - подібну форму (два вигини), використовують рівняння параболи третього порядку:

у, = а₀ + а₁- + а₂-² + а₃-³.

4) якщо коефіцієнти зростання, розраховані по відношенню до попереднього періоду, більш чи менш постійні, тобто ряд динаміки відображує розвиток у геометричній прогресії, розраховують показову функцію. Для вирівнювання ряду динаміки в

даному випадку використовують рівняння ^у< ^{= аоа}<.

Логарифм показової функції (^lgу< ^{= lgа}" ⁺< ^lgаі) являє собою рівняння прямої. Параметри ^а° і ^а знаходять за системою нормальних рівнянь:

п lg ^ао + lg ^а_х £ < = 2 lg ^у {lg а₀ 2 < + lg а: £ < < = £ < lg У

5) серед інших способів обробки рядів динаміки особливе місце займає вирівнювання за допомогою ряду Фур'є, який

у< = а₀ + ^(а_к cos к< + вк sin к<)

виражається рівнянням: "⁼¹

2 у ²Z у^{cos к}<

де к - гармоніка ряду (к=1; к=2; і т.д.) ; " ; " ;

2У у sin к<

п

Параметри аналітичного рівняння лінії зв'язку визначають за способом найменших квадратів. Тобто, сума квадратів відхилень фактичних рівнів динаміки від вирівняних повинна бути

o o У (У, - У ) = min

мінімальною: ^ < < .

Вирівняні рівні ряду (^у<) розраховують на підставі аналогічного рівняння шуканої прямої чи кривої. На графіку вони розташовані на прямій чи кривій лінії відповідного типу.

Таким чином, якщо розглядати технічний бік вирівнювання, то він зводиться до заміни фактичних рівнів теоретичними, які в середньому мінімально відхилися б від фактичних рівнів, але мали б певний аналітичний вираз.

Хоча спосіб вирівнювання ряду динаміки містить в собі певні умовності, в ряду випадків він є досить корисним технічним прийомом, який полегшує виявлення загальної тенденції і вивчення характеру ряду динаміки. Зокрема, це стосується вивчення сезонних коливань. Про це мова йтиме пізніше.

Приклад. Розглянемо найбільш поширеного і простого випадку аналітичного вирівнювання ряду динаміки врожайності проса за рівнянням

прямої лінії (1987-2004 рр., "=18). Рівняння прямої має вигляд ^у< ~ ^а° ^{+ а}<, де t час, тобто порядковий номер періоду або моменту часу; ^а° і ^а1- параметри шуканої прямої.

Параметри ^а<0 і ^а знаходяться за системою нормальних рівнянь:

К Е^і+^а1 Е^{і 2} =Е ^у

де у - фактичні рівні ряду; и= число рівнів.

Для зручності розрахунків будують робочу таблицю 61. На підставі даних цієї таблиці одержуємо таку систему нормальних рівнянь:

Ґ18а₀ + 171а₁ = 263,9 |Ша₀ + 2109^ = 2959,1

Рішення:

171а₀ + 2109а₁ = 2959,1 - 171а₀ +1624,5^ = 2507,1 484,5а₁ = 452_;

а₁=0 93_; 18"₀ + (171 х 0,93) = 263,9; а₀₌₌ =5 80

Знайдені параметри дають змогу побудувати рівняння прямої: ^Уі =5,8 + 0,93 і

Таблиця 61

Вихідні та розрахункові дані вирівнювання ряду динаміки врожайності проса за рівнянням прямої

Дані одержаного рівняння свідчать про те, що середня врожайність проса в нульовому році (1986) досліджуваного періоду становила 5,8 ц , а підвищення її складає в середньому 0,93 ц у кожному наступному році, тобто теж саме означає середньорічний приріст урожайності впродовж досліджуваного періоду.

Підставивши в рівняння почергово значення 1, одержуємо вирівняний ряд динаміки врожайності, який абстрагований від випадкових коливань і характеризується систематичним підвищенням рівнів.

В аналогічній послідовності здійснюється вирівнювання рядів динаміки за іншими типами аналогічних функцій (парабола, гіпербола, експонента та ін.).