Математична статистика - Руденко В.М. - Згруповані розподіли

Розподіли згрупованих частот використовуються у разі інтервальних або відносних типів вимірювань, якщо емпіричні дані приймають будь-які дійсні значення в певному інтервалі або кількість варіант близька до обсягу вибірки. У цій ситуації змінні мають бути представлені інтервалами (або класами) значень однакової довжини.

Приклад 2.4. Розрахувати розподіли коефіцієнта інтелекту IQ вибірки обсягом у 80 осіб за емпіричними даними у балах (див. таблицю рис. 2.12)

Послідовність рішення:

o характер емпіричних даних показує, що необхідно розрахувати розподіли згрупованих частот;

o знайти мінімальне і максимальне значення IQ у комірках C12 і G12 за допомогою функцій MS Excel =МИН(Л2:И11) і =МАКС(Л2:Н11), отримати відповідно IQ_min =72 і IQmca =137 (рис. 2.12);

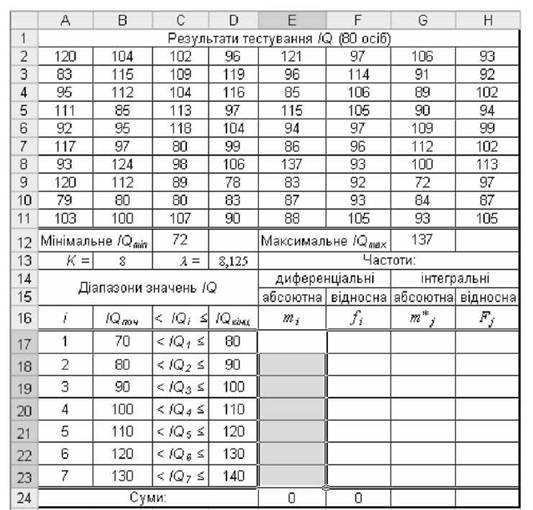
Рис. 2.12. Внесення емпіричних даних і функції =ЧАСТОТА()

o розрахувати кількість класів к за формулою Стерджеса Л"=1+3,32-Ьз п , де п - обсяг вибірки. Для цього внести у комірку В13 вираз =ОКРВВЕРХ(1+3,32*тв10(СЧЕТ(А2:Н11));1) і отримати К~ 8;

o розрахувати розмір класового інтервалу л=( І<2_мах - І(2гпт)/к у комірці Б13 за допомогою виразу =(в12-С12)/Б13. Хоча отримане значення X = 8,125, але з практичної точки зору доцільно розмір класового інтервалу прийняти X = 10;

o розрахувати у комірках А17:Б23 значення початкової І))"_оч і кінцевої і(2кінц границь діапазонів значень І) кратними 10 балам і так, щоб мінімальне значення І<2_міп = 72 входило у перший, а максимальне І<2_мах = 137 - в останній інтервал (див. рис. 2.12);

o виділити діапазон Е17Е23, натиснути клавішу і за допомогою "Майстра функцій" внести у ці комірки функцію =ЧАСТОТА();

o задати аргументи функції =ЧАСТОТА(), як показано на рис. 2.13;

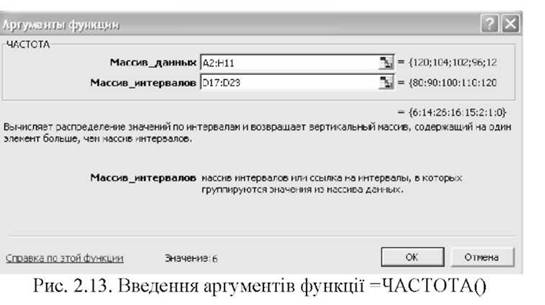
o натиснути разом клавіші ЄТЯЬ+8ИІРТ+ЕКТЕЯ, отримати у комірках Е17:Е23 значення абсолютних диференціальних частот (рис. 2.14);

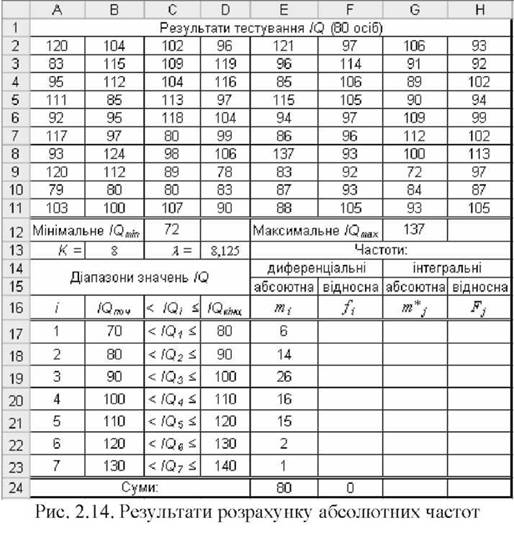
o для розрахунку диференціальних відносних, інтегральних абсолютних і відносних частот внести у комірки Р17:И23 відповідні формули (рис. 2.15);

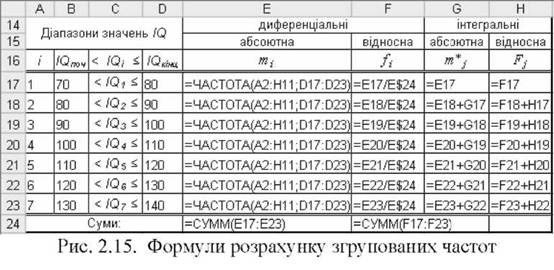
o отримати результати розрахунку згрупованих частот І) (рис. 2.16) і побудувати графіки розподілу (рис. 2.17).

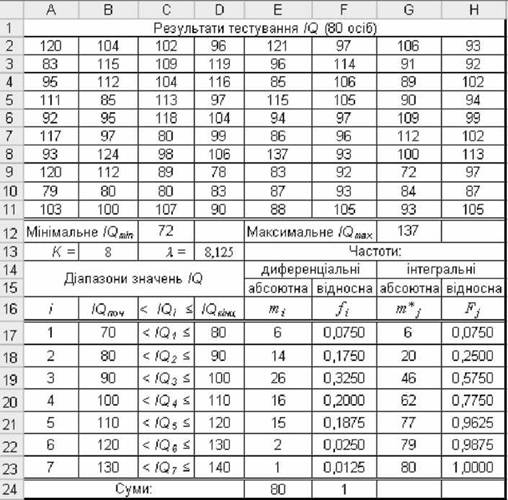
Рис. 2.16. Результати розрахунку розподілу результатів тестування І)

Графіки диференціального та інтегрального розподілу І) за інтервалами значень показано на рис. 2.17.

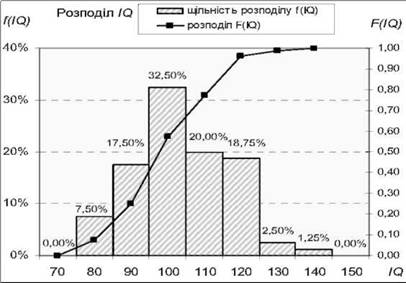
Рис. 2.17. Графіки розподілу Щ

Диференціальний відносний розподіл - щільність розподілу од2) - зображений гістограмою. Він дає загальну картину розподілу як усіх категорій разом, так і кожної категорії окремо. Як бачимо з рис. 2.17, цей розподіл має форму, що нагадує теоретичний нормальний розподіл (проте, необхідно коректно довести їхню ідентичність). Максимум розподілу - 32,5% - припадає приблизно на середину графіка на значення 1(2 у 100 балів; 1,25% від загального обсягу вибірки складає категорія "обдарованих" з 1(2 д° 140 балів і 7,5% - категорія "нижче середнього". Графік розподілу унімодальний і асиметричний, щільність концентрується навколо середніх значень.

Інтегральний відносний розподіл ?(І(2) зображений точками. Він дає можливість отримати сумарні показники частот для різних діапазонів І(. Наприклад, з графіка і таблиці рис. 2.16 видно, що особи з 1(2 < 100 (не вище 100 балів) становлять 57,5% від загального обсягу вибірки, а особи з 1(2 > 120 (вище 120 балів) складають лише 3,75% від обсягу вибірки (знаходимо або з таблиці, або з графіка: 100% - 96,25% = 3,75%).

Крім варіаційних (незгрупованих і згрупованих) розподілів у практиці досліджень розраховують атрибутивні і ранжирувані розподіли, яки використовують для описової характеристики значення так званих "якісних" емпіричних даних, що виміряні за порядковими та номінальними шкалами.