Математична статистика - Руденко В.М. - Початкові та центральні моменти

Розрахунки показників МЦТ і ММ можна здійснити в MS Excel трьома способами з використанням:

o математичних операцій за відповідних формул МЦТ і ММ;

o вбудованих статистичних функцій MS Excel;

o спеціального розділу "Описова статистика" пакету "Аналіз даних". Спосіб 1. Результати розрахунку МЦТ і ММ представлено на рис. 2.37,

відповідні математичні вирази, формули і функції MS Excel - на рис. 2.38 .

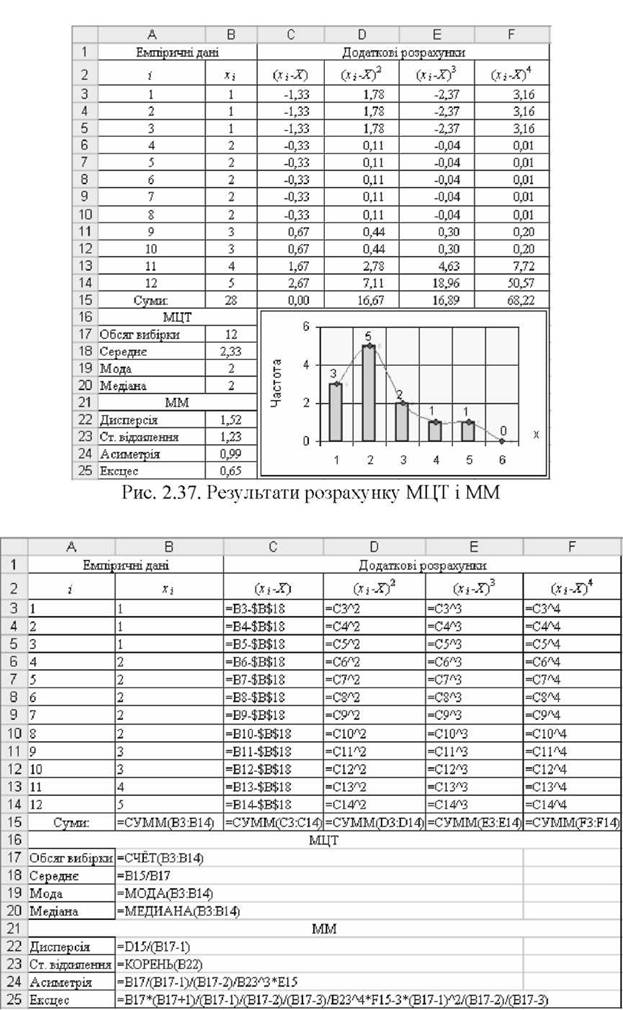
Рис. 2.38. Математичні вирази для розрахунку МЦТ і ММ

Мода вибірки Мо=2 (значення 2 трапляється у вибірці 5 разів). Медіана дорівнює

Мй - ^Хп/2 ^{+ Х}п/2+1 _ ^Х12/2 ^{+ Х}12/2+1 _ ^Х6 ^{+ Х}7 _ ² + ² _ ⁴ _ 2

~ 2 2 ~ 2 ~ 2 ~2~ ^.

Середнє арифметичне вибірки X = - v х_і = - 28 = 2,33.

п 12

Дисперсія вибірки ^у2 = ^⁽_п'_1 ⁾ = 1^ = ~ ^1,52 .

Стандартне відхилення вибірки у_х =^[^ї = 1,52 "1,23. Асиметрія вибірки

Спосіб 2. Результати розрахунків показників описової статистики для чотирьох вибірок представлено на рис. 2.39, графіки розподілу - на рис. 2.402.43. Для розрахунків були використані такі статистичних функцій MS Excel:

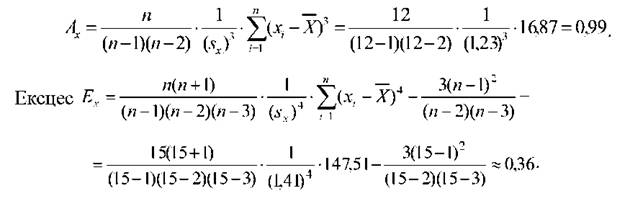
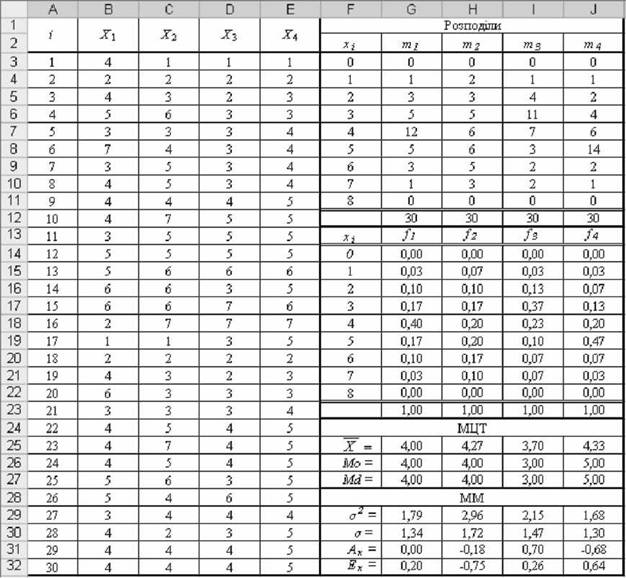
Рис. 2.39. Розрахунки розподілу, МЦТ і ММ за допомогою функцій табличного процесора MS Excel

Розподіли розраховано за допомогою функції =ЧАСТОТА() і представлено на рис 2.40-2.43.

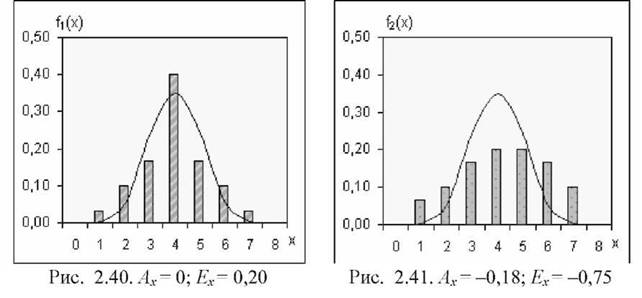
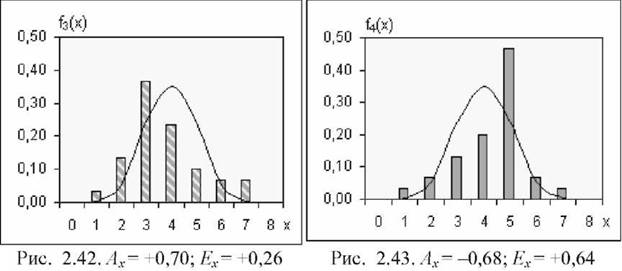
Як видно, всі вибірки унімодальні, характеризуються приблизно однаковими МЦТ (див. комірки F25:J27). Розподіл вибірки f₁(x) має нульову асиметрію (0,00), малий додатний ексцес (0,20) і серед чотирьох вибірок найбільш відповідає властивостям нормального розподілу (рис. 2.40).

Розподіл f₂(x) характеризується незначною від'ємною асиметрією (-0,18) і суттєвим від'ємним ексцесом (-0,75) (рис. 2.41). Розподіл f₃(x) "деформований" у лівий бік з асиметрією (0,70) і помірним додатним ексцесом (0,26) (рис. 2.42). Розподіл f4(x) має від'ємну асиметрію (-0,68) ще й додатний позитивний ексцес (0,64). У порівнянні зі "стандартом" він менш за все відповідає вимогам нормальності серед досліджуваних вибірок.

Спосіб 3. Отримати показники МЦТ і ММ вибірки за допомогою пакета "Аналіз даних" розділ "Описова статистика" можна у такій послідовності дій:

o виконати команди головного меню Excel [Сервіс -> Аналіз даних], вибрати розділ "Описова статистика (рис. 2.44), викликати діалогове вікно;

Рис. 2.44. Розділ "Описова статистика"

o встановити у діалоговому вікні "Описова статистика" (рис. 2.45) вхідні дані та параметри виводу, виконати команду ОК і отримати результати у комірках стовпчиків С:Б (рис. 2.46);

Рис. 2.45. Параметри діалогового вікна

o порівняти результати з розрахунками емпіричних МЦТ і ММ попереднього способу 1 (рис. 2.37), зробити висновки.

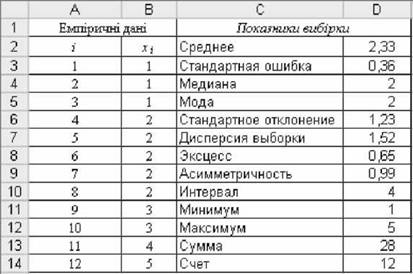
Рис. 2.46. Результати розрахунку основних показників описової статистики

Отже, серед розглянутих способів розрахунку статистик (показників МЦТ і ММ), найбільш ефективним і гнучким вважаються засоби з використанням вбудованих статистичних функцій табличного процесора MS Excel.

Початкові та центральні моменти

Для системної характеристики варіаційного ряду використовують спеціальні показники - початкові та центральні моменти.

Початковий момент к-то порядку варіаційного ряду визначається як:

п

^vk =е^хк * Їі . (2.13)

Центральний момент к-то порядку визначається за формулою:

п _

^тк =е^(х "^х)к *Л , (2.14)

і=і

де Хі - варіанти розподілу; /_і - диференціальні відносні частоти, x - середнє арифметичне.

Очевидно, що перший початковий момент (к=1) має сенс середнього арифметичного варіаційного ряду

п _

^т1 =х^хі " -/і = ^х . (2.15)

Перший центральний момент (к=1) дорівнює нулю, що зумовлено властивостями середнього

п _

т =е (х - х) ■ /і = о. (2.16)

Другий центральний момент (к=2) - це дисперсія ¡1 варіаційного ряду

п _

^т2 =е^(х ~^х)2 ■ /і = ^ях². (2.17)

Третій центральний момент (к=3) характеризує асиметрію розподілу

тз = £(Хі - X)³/_і .

Якщо розділити третій центральний момент т₃ на куб середньоквадра-тичного відхилення (я_х)³, то отримаємо коефіцієнт асиметрії розподілу ^4_х:

7% £ ^(х - ^{Х)3 У} = ^А* . (2.18)

С⁵*⁾ С⁵*⁾ 1=1

Четвертий центральний момент т₄ дає можливість оцінити "загостреність" варіаційного ряду, тобто оцінити ексцес

т4 = £(х, - X)⁴/ . Коефіцієнт ексцесу Е_х визначається через 4-й центральний момент т₄ :

-³-[5^(х;-^Х)3Л]-³-^{Ех (2.19)}

Між центральними і початковими моментами існує зв'язок: ^т! = 0;

що витікає з перетворень:

п п п п

т₂ =£(X "X)²/ =е(*² "2х,Х + X v, =£х²У) -е(2х,Х-X²)/_і = і=і і=і і=і і=і

= у_г -х(х,Х+х~Х-X²)/і = у_г -Х%/ -Х£(х, -X)/; ^2 -^ -0 = у_г -V²

і=1 і=1 і=1

п п

Отже, якщо т₂ = ^v2 =е ^хі ' ї; , ^vl =е^х;' ї; , то можна отримати ще одне співвідношення, яке використовується для розрахунку дисперсії:

п ( п ²

і=1 v і=1 )

Центральні моменти 3-го і 4-го порядку теж можна записати за допомогою початкових моментів:

т₃ = v₃ - 3^₂ + 2v³, (2.20)

т₄ = v₄ - 4^₃ + 6v₁²v₂ - 3v⁴ і т.д.

Практика статистичних досліджень обмежується, як правило, використанням моментів до 4-го порядку.

На основі порівняння значень теоретичних і вибіркових моментів виконується оцінювання параметрів розподілів випадкових величин (див., наприклад, розділ 4 "Методи статистичного оцінювання").