Математична статистика - Руденко В.М. - Нелінійна кореляція

Приклад 2.8. Оцінити зв'язок між віком (змінна X) і результатами допоміжного тесту "цифра-знак" шкали інтелекту дорослих Векслера (змінна Y). Упорядковані за віком дані 15 осіб представлено у таблиці рис. 2.58.

Послідовність рішення:

o оцінити характер лінійності (нелінійності) зв'язку між значеннями ознак віку (X) і тесту (Y) за допомогою діаграми розсіяння (рис. 2.57);

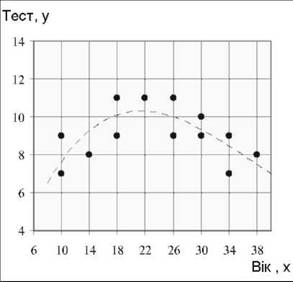
Рис. 2.57. Діаграма розсіяння ознак

o переконатися, що кореляція нелінійна - спочатку результати тестування круто зростають для осіб віком від 10 до 22 років, досягають максимального значення, а потім повільно зменшуються. Якісна картина дає підстави для застосування кількісної міри нелінійності - кореляційного відношення, чисельне значення якого знаходиться у межах від 0 до 1:

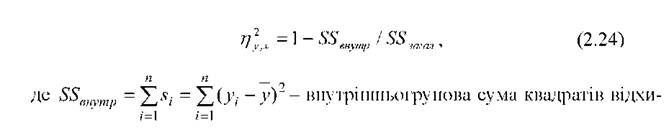
лень у і від середнього у; 5Б_загап = s _у ■ (п -1) - загальна сума квадратів;

o розрахувати квадрати різниць s¡ окремо для кожної вікової групи (вікові групи виділено зафарбованими рядками, результати розрахунків і відповідних формул показано на рис. 2.58 і 2.59);

o внести у комірку вираз =(С3-СРЗНАЧ($С$3:$С$4))^Л2. Аналогічний вираз внести у комірки (вікова група 10 містить лише два значення тесту);

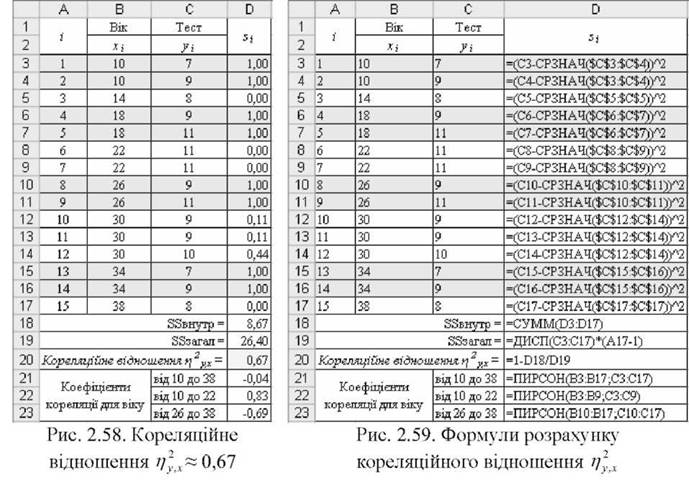
o визначити Si для інших вікових груп, де х = 14, 18, 22, 26, 30, 34 і 38;

o у комірці Б18 розрахувати 88_внутр (вираз =СУММ(03:017));

o у комірці Б19 розрахувати 88_шгал (вираз =ДИСП(С3:С17)*(А17-1));

o у комірці Б20 отримати відношення п²_ухс (внести вираз =1-018/019);

o у комірці Б21 розрахувати коефіцієнт кореляції Пірсона для всього масиву за допомогою функції MS Excel =ПИРСОН(В3:В17;С3:С17). Коефіцієнт кореляції дорівнюватиме приблизно нулю (r_xy ~ -0,04), що свідчить про (нібито) відсутність будь-якого зв'язку між змінними;

o розрахувати коефіцієнти кореляції окремо для частин масиву: у комірці D22 для віку від 10 до 22, у комірці D23 для віку від 26 до 38 .

Отже, для віку від 10 до 22 років коефіцієнт кореляції має високе додатне значення (r_xy=+0,83), що підтверджує прямий зв'язок, який можна спостерігати на діаграмі. Для віку від 26 до 38 років коефіцієнт кореляції має від'ємне значення (^=-0,69), що інтерпретується як зворотний зв'язок. Значення кореляційного відношення " 0,67 підтверджує високій рівень не лінійності зв'язку змінних X Y.

Слід звернути увагу на те, що для коефіцієнта rf_yxc спочатку вказують індекс у, а потім - х, який є мірою прогнозування Y по X. Важливо зазначити, що для лінійного кореляційного зв'язку виконується співвідношення r_xy = r_yx, проте rf_yxc і rf_xyy матимуть різні значення. Якщо звернутися до діаграми розсіяння (рис. 2.57), то можна відзначити той факт, що для особи, наприклад, віком 10 років (Х=10), можна прогнозувати середню оцінку тесту у 8 балів (Y=(7+9)/2=8), у той час як для оцінки тесту, наприклад, у 8 балів вік особи може бути як близько 10, так і близько 38 років.

Розрахунки важливих для психолого-педагогічних досліджень коефіцієнтів кореляції приведено разом з оцінкою їхньої вірогідності у розділі 5.6.

Коефіцієнти взаємної зв'язаності

Коефіцієнти взаємної зв'язаності, наприклад, Чупрова K і Пірсона С застосовуються для оцінки зв'язку у ситуаціях, коли кожна якісна ознака складається більш ніж з двох груп. Коефіцієнт Чупрова К використовується у разі неоднакової кількості рядків і стовпчиків таблиці спряженості (k, Ф k2):

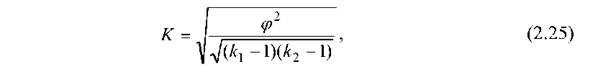
де к_] і к₂ - кількість груп першої і другої ознаки (параметри xі У). Коефіцієнт взаємної зв'язаності Пірсона с застосовується, коли кількість рядків і кількість стовпців у таблиці спряженості збігаються (к_; = к₂):

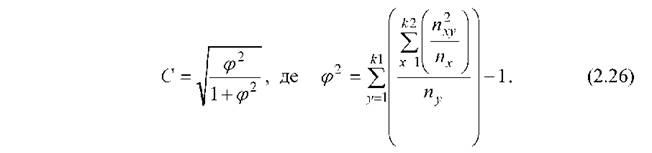
Значення коефіцієнтів Чупрова К і Пірсона с змінюються від 0 до 1. Приклад 2.9. Оцінити зв'язаність між приналежністю осіб до певної соціальної групи та їх психічними станами (табл. 2.5).

Таблиця 2.5

Розподіл груп за психічними станами

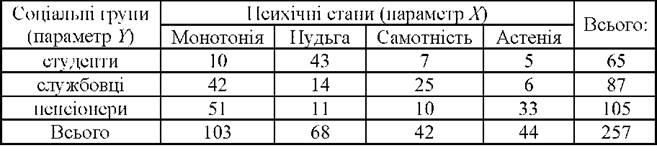
Послідовність рішення:

o Для ситуації з неоднаковою кількістю рядків і стовпчиків (к_; Ф к₂) використати коефіцієнт взаємної зв'язаності Чупрова К.

o Внести емпіричні дані у таблицю рис. 9.20 і виконати такі дії: - розписати докладніше вираз <р², виходячи з умов к, = 3 і к₂ = 4:

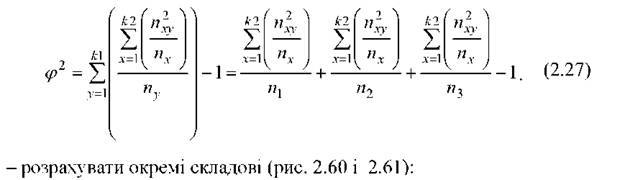
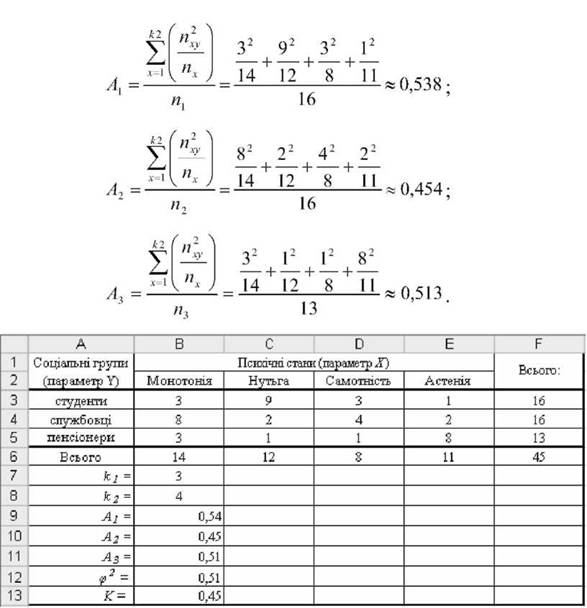
Рис. 2.60. Результати розрахунку коефіцієнта Чупрова К

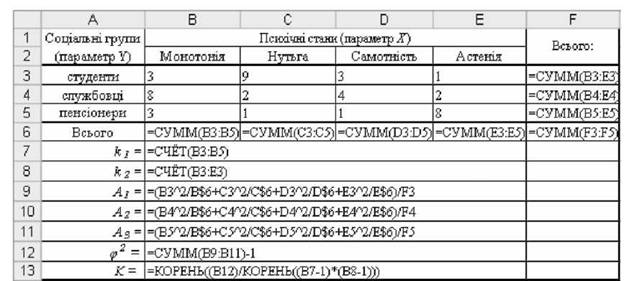
Рис. 2.61. Формули для розрахунку коефіцієнта Чупрова К

- визначити параметр ф²:

<р² = 0,538+0,454+0,513-1 = 0,505. - отримати чисельне значення коефіцієнта взаємної зв'язаності Чупрова К

К -і = , ^ 0,45.

У(к1 - 1)(к2 -1) V л/(3 " 1)(4 -1)

Висновки. Значення коефіцієнта Чупрова К ~ 0,45 свідчить про помірну взаємну зв'язаність між параметрами У і x. Направлення зв'язаності коефіцієнт К не вказує. Це можна оцінити за формою спільного розподілу.

Запитання. Завдання.

1. Що таке кореляція? Охарактеризуйте особливості кореляційного зв'язку^.

2. Які види зв'язків (три типи залежностей) між змінними X і У можна виділити?

3. Доведіть, що вибірковий коефіцієнт кореляції є випадковою величиною.

4. Який кореляційний зв'язок називають прямим, а який - зворотним?

5. Як якісно оцінити лінійність (нелінійність) кореляції?

6. В яких межах знаходиться чисельне значення коефіцієнтами кореляції?

7. Як кількісно оцінити лінійність (нелінійність) кореляції?

8. Запишіть формулу коефіцієнта лінійної кореляції Персона.

9. В яких межах знаходиться чисельне значення кореляційного відношення?

10. Охарактеризуйте особливості використання коефіцієнтів взаємної зв'язаності Чупрова К і Пірсона С.

11. В яких межах знаходиться значення коефіцієнтів взаємної зв'язаності Чупрова К і Пірсона С?

12. Повторіть математичні процедури завдань за прикладами 2.7 - 2.9.

13. Виконайте лабораторні роботи № 4 - № 6.