Математична статистика - Руденко В.М. - Дисперсія випадкової величини

Математичне сподівання показує, навколо якої чисельної міри групуються значення випадкової величини. Проте, необхідно також мати можливість вимірювати мінливість (варіативність) випадкової величини щодо математичного сподівання. Таким показником мінливості є математичне сподівання квадрату різниці між випадковою величиною та її математичним сподіванням, а саме M[(X - М[Х])² ].

Означення. дисперсією випадкової величини x називається число¹⁴ DX] = M[(X-M[X])²], (3.30)

або DX] = ±f(x_t) o(*, - M[X])².

На рис.3.26 наведено формули для розрахунку розподілу - статистичної ймовірності fx;) - а також показників: математичного сподівання М[Х] (комірка Е9) і дисперсії D[X] (комірка G9).

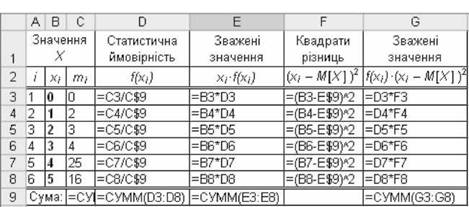
¹⁴ Пропонуємо порівняти це означення з означенням вибіркової дисперсії

s².

Рис. 3.26. Формули розрахунку м[х] і 0[Х] У таблиці рис.3.27 показано результати розрахунку математичного сподівання м[х] і дисперсії 0[Х] за даними приклада 3.14, а також гістограму розподілу м[х] = 4,00 (комірка Е9) і дисперсія 0[Х] = 1,00 (комірка в9).

Математичне сподівання показує, що значення випадкової величини x групуються біля значення 4,00, кількість яких становить 50% від загальної кількості. Проте, навколо такого ж значення можуть групуватися й інші дані.

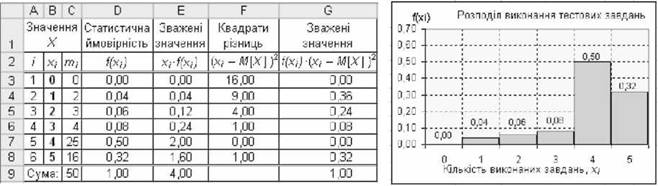
Рис. 3.27. Таблиця і гістограма розподілу з А/[Х]=4,00 і £>[Х]=1,00

З рис.3.28 видно, що для математичного сподіванням[х] = 4,00 дисперсія £>[Х] = 2,32 є удвічі більшою, ніж за даними рис. 3.27. Про значну мінливість свідчить й відповідна гістограма.

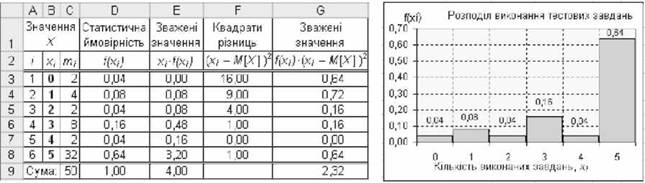
Рис. 3.28. Таблиця і гістограма розподілу з М[Х]=4,00 і £>[Х]=2,32

Пропонуємо порівняти таблиці і графіки рис. 3.27 і 3.28 і зробити висновки. Властивості дисперсії випадкової величини, які постійно використовуються у ймовірносно-статистичних методах:

o якщо x - випадкова величина, а і Ь - деякі числа, У = ах+Ь, то

D[ax+b] = a²D[X] (3.31)

(це значить, що число а як параметр масштабу суттєво впливає на дисперсію, тоді як число b - параметр зсуву на значення дисперсії не впливає);

o якщо X₁, X₂, X_n - попарно незалежні випадкові величини (тобто X_t і X незалежні для i Ф j ), то дисперсія суми дорівнює сумі дисперсій

D[X₁ + X₂ + ... + X_n] = D[X₁] + D[X₂] + ...+D[X_n]. (3.32)

Співвідношення щодо математичного сподівання (3.25) і дисперсії (3.32) мають важливе значення при вивченні вибіркових властивостей, оскільки результати вибіркових спостережень або вимірів розглядаються в математичній статистиці, як реалізації незалежних випадкових величин.

З дисперсією випадкової величини тісно зв'язаний ще один показник мінливості - стандартне відхилення.

Означення. Стандартним відхиленням випадкової величини x називається невід'ємне число

SD[ X ] = +VD[X]. (3.33)

Отже, стандартне відхиленнях однозначно зв'язано з дисперсією.

У теорії та практиці статистичних досліджень також важливу роль відіграють спеціальні функції - так звані моменти (початкові і центральні), які є характеристиками випадкових величин.

Означення. Початковим моментом k-то порядку випадкової величини x називається математичне сподівання k-ї степені цієї величини:

~_k = M[ X^k ].¹⁵ (3.34)

Означення. Центральним моментом k-то порядку випадкової величини x називається математичне сподівання k-ї степені відхилення цієї величини x від його математичного сподівання:

m = m[x - M(X)Y, (3.35)

або m_k = M[X - a]^k, де a = M[X].

Для позначення мометнів випадкових величин використовуємо ті ж самі літери, що і для мометнів варіаційного ряду, але з додатковим знаком ~ ("тільда").

Формули для обчислення моментів дискретних (які приймають значення Хі з імовірністю р,) і неперервних (зі щільністю ймовірності /х)) випадкових

величин наведено у табл. 3.4.

Таблиця 3.4

Формули для обчислення моментів випадкових величин

Як і для варіаційних рядків моменти дискретних випадкових величин мають аналогічний сенс:

Перший початковий момент (¿=1) випадкової величини Хе її математичним сподіванням:

~1 = М[Х] = ц. (3.36)

Другий центральний момент (¿=2) визначає дисперсію 0[Х] випадкової величини x:

Ш_г (хі - а)² р_і = ЦХ] = (Т². (3.37)

Третій центральний момент (¿=3) характеризує асиметрію розподілу випадкової величини x:

п

Коефіцієнт асиметрії а розподілу випадкової величини x має вигляд:

-Г = ~X(хі " а)³Рі = А. (3.38)

Четвертий центральний момент (¿=4) характеризує крутість розподілу випадкової величини.

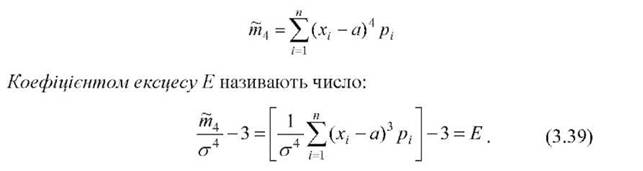
На основі порівняння значень теоретичних і вибіркових моментів виконується оцінювання параметрів розподілів випадкових величин (див., наприклад, розділи 4 і 5).

Як відзначалося вище, в математичній статистиці використовуються два паралельних рядка показників: перший - має відношення до практики (це показники вибірки), другий - базується на теорії (це показники імовірнісної моделі). Співвідношення цих показників представлено у табл. 3.5.

Таблиця 3.5

Співвідношення показників емпіричної вибірки й імовірнісної моделі

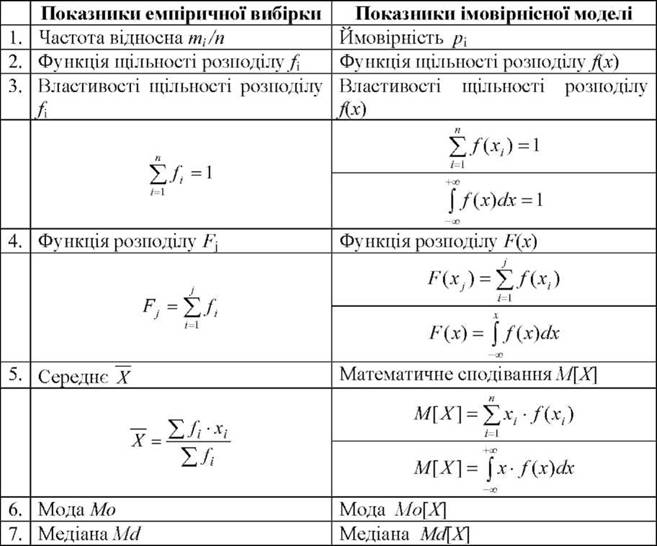
Таблиця 3.5 продовження

Отже, метою описової статистики є перетворення сукупності вибіркових емпіричних даних на систему показників - так званих статистик, що мають відношення до реально існуючих об'єктів. Так, психологи, педагоги, інші фахівці працюють у реальній сфері, об'єктами якої є особи, групи осіб, колективи, характеристиками для яких служать емпіричні показники. Проте основна мета дослідження - це здобуття нового знання, а знання існує в ідеальній формі у вигляді характеристик теоретичних моделей. Звідси виникає проблема коректного переходу від емпіричних показників реальних об'єктів до показників теоретичної моделі. Цей перехід потребує аналізу як загальних методичних підходів, так і строгих математичних підстав. Принципову можливість тут відкриває закон великих чисел, теоретичне обгрунтування якому було надане Якобом Бернуллі (1654-1705), Пафнутієм Львовичем Чебишевим (1821-1894) та іншими математиками XIX ст.

Запитання. Завдання.

1. Розкрийте поняття випадкової величини.

2. Чим відрізняються дискретна і неперервна випадкові величини?

3. З яких елементів складається імовірнісний простір?

4. Як побудувати розподіл дискретної випадкової величини?

5. Як зв'язані між собою функція щільності Л(х) і функція розподілу Б(х)?

6. Надайте геометричну інтерпретацію інтегралові Б(со) = | Л(х)сх = 1.