Зміст класичних законів великих чисел полягає в тому, що вибіркове середнє арифметичне незалежних однаково розподілених випадкових величин наближається (сходиться ) до математичного сподівання цих величин. Іншими словами, вибіркові середні сходяться до теоретичного середнього.
Біноміальний розподіл
Більшість завдань теорії ймовірностей припускають відомими із самого початку ймовірності елементарних випадкових подій (наприклад, усі ймовірності складають по 0,5). Спираючись на знання цих ймовірностей, розраховують імовірнісні характеристики складних подій.
Наприклад, кожний іспит одного студента (кожна подія Г) складається з шести елементарних подій а>,- (результатів виконання завдань), тобто 1={ю1, ю2, юп), де п = 6. Кожна елементарна подія а>,- має лише два наслідки: прямий (бажаний) - "виконано" (або "1") і протилежний (небажаний) - "не виконано" (або "0"). Розглянемо варіант так званого "байдужого" студента, який намагається скласти іспит, відповідаючи навмання на завдання. Тоді можна прийняти, що елементарні події матимуть однакові ймовірності: /?(1)=/>(0)=1/2=0,5. Для спрощення математичного викладу ймовірність бажаної елементарної події позначимо якр, тобто р(1) = р. Тоді:
р(1) = р = 0,5 ;
р(0) = 1-/Х1) = = 1 - 0,5 = 0,5.
Кількість бажаних елементарних подій (виконаних завдань) т може коливатися від 0 (жодного виконаного завдання) до 6 (усі завдання іспиту виконано). Розрахуємо ймовірності того, що в складній події / з п елементарних подій а>і можна отримати т "бажаних" наслідків з імовірністю р і, зрозуміло, п-т "небажаних" наслідків з імовірністю
Загальна ймовірність однієї такої складної події / дорівнює добутку ймовірностей незалежних елементарних подій і обчислюється як: pm ■ (1 - p) "-m.
Проте кількість варіантів складних подій / з n елементів по m визначається кількістю комбінацій: C'm =-.
n m!(n - m)!
Тому остаточно загальну ймовірність спостереження складної події / можна розрахувати за формулою Бернуллі:
P(m) = Cm o pm o (1 -p)n-m. (3.56)
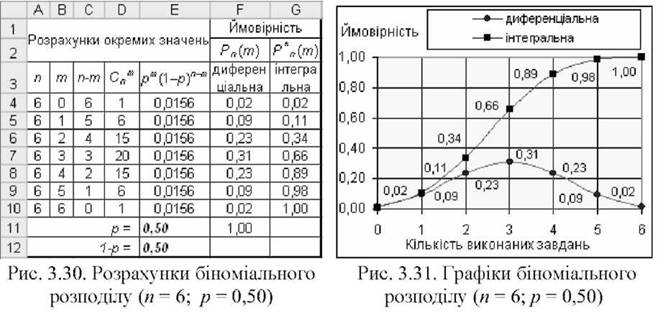
Ця формула визначає теоретичний розподіл ймовірностей складних подій - так званий біноміальний розподіл. На рис. 3.30 наведено його розрахунки для параметрів n = 6,p = 0,5; на рис. 3.31 - графіки диференціальної та інтегральної функцій розподілу ймовірностей. Необхідно мати на увазі, що біноміальний розподіл - це розподіл дискретної змінної.
Для розрахунків біноміального розподілу зручно використовувати функцію =BHHOMPACn(m; n; p; І), що входить до складу MS Excel. Функція повертає дискретні значення розподілу, де m - кількість успіхів; n - загальна кількість випробувань; p - ймовірність успіху; І - параметр, який визначає тип розподілу (1 - інтегральна функція, 0 - диференціальна функція розподілу).
Розподіли можна розрахувати і для інших апріорних ймовірностей бажаних елементарних подій. Припустимо, що для "слабкого" студента ймовірність р бажаної події складає, наприклад, 30% або 0,3. На рис. 3.32 наведено відповідні розрахунки для п = 6, р = 0,3; на рис. 3.33 - графіки диференціальної та інтегральної функцій розподілу.

Для "сумлінного" студента ймовірність р елементарної бажаної події складатиме більше 50%, наприклад, 70% або 0,7. На рис. 3.34 і 3.35 наведено розрахунки для п = 6,р = 0,7, а також відповідні графіки розподілу.
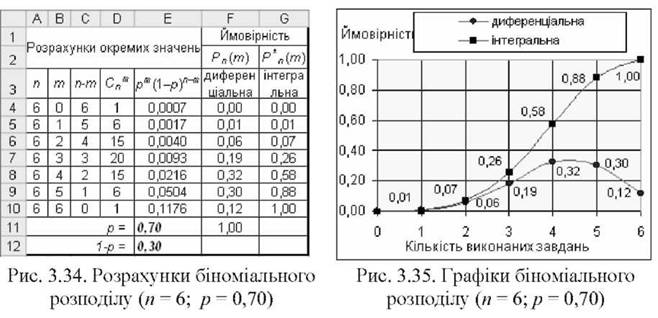
Різницю між біноміальними розподілами для різних значень ймовірностей елементарних бажаних подій можна спостерігати на відповідних графіках. Пропонуємо самостійно прокоментувати рис. 3.31, 3.33 і 3.35.
Основні показники центральної тенденції і варіативності для біноміального розподілу визначаються так:
o середнє арифметичне X = п o р;
o дисперсія sу = п ■ р ■ (1 - р);
o стандартне відхилення sI =л[^ї.
На рис. 3.36 у табличній формі показана залежність цих показників розподілу від ймовірності р елементарної бажаної події.
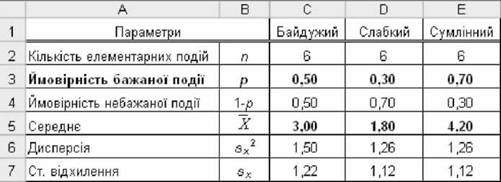
Рис. 3.36. Залежність МЦТ і ММ від ймовірності подіїр
Як бачимо з таблиці рис. 3.36, для "байдужого" студента (р = 0,5) середнє значення складає 3 бажаних події, для "слабкого" (р = 0,3) - в середньому 1,8 бажаних подій; для "сумлінного" студента (р = 0,7) - в середньому 4,2 бажаних подій з 6 можливих.
На прикладі біноміального розподілу можна продемонструвати загальну методику використання теоретичних функцій розподілу в рішенні реальних практичних завдань.
Приклад 3.19. У таблиці рис. 3.37 розраховано розподіл за емпіричними даними (іспити студентів за тестами) і теоретичний біноміальний розподіл з ймовірностями успіху р(1) = 0,50 і неуспіху р(0) = 1-р(1) = 1-0,50 = 0,50.
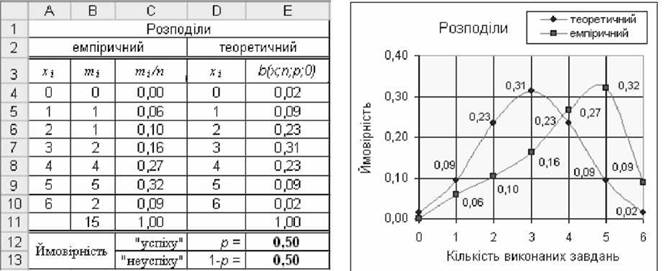
Рис. 3.37. Емпіричний і теоретичний розподіли
Як видно з рис. 3.37, графік емпіричного розподілу "реальної ситуації" суттєво відрізняється від теоретичного так званого варіанту "50/50". Це дає підстави сподіватися на те, що реальні результати іспитів зумовлені більшою ймовірністю "успіхів" елементарних подій, тобто р(1) > />(0).
Математично реальну здатність студентів до успішного виконання завдань (що зумовлюють компетентність, мотивація, інтелект або інші чинники) можна зафіксувати через невідому (поки що) ймовірність р *. Знайти ймовірність р* можна навіть простим добором (збільшуючи або зменшуючи) значення показника ймовірності р так, щоб наблизити ("підтягнути") графік теоретичного розподілу до графіка емпіричного розподілу. Зрозуміло, що таке наближення "ручним" шляхом не є ефективним.
Завдання: визначити ймовірністьр*.
Рішення:
Оптимального значення ймовірності р* можна досягти з використанням комп'ютерних інтерактивних можливостей MS Excel у такій послідовності:
o за допомогою миші активізувати і наблизити донизу точку графіка теоретичного розподілу зі значенням, наприклад, 0,31 до точки емпіричного розподілу зі значенням 0,16 (див. рис. 3.38).
o внаслідок цього з'явиться діалогове вікно "Добір параметра", в якому встановити відповідні значення параметрів, як зображено на рис. 3.39;
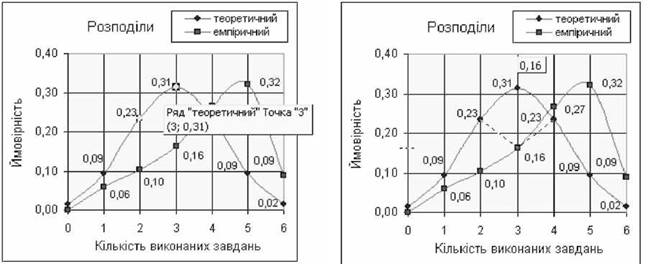
Рис. 3.38. Наближення теоретичного розподілу до емпіричного o після команди ОК отримати повідомлення про результат добору параметра - "Рішення знайдено" (рис. 3.40);

o в результаті у комірці Е12 з'явиться нове перераховане значення ймовірності р, яке дорівнюватиме 0,72, а в електронній таблиці - відповідні перераховані значення теоретичної функції. Зміниться також і форма графіка цієї функції, який наблизиться до графіка емпіричного розподілу (рис. 3.41).
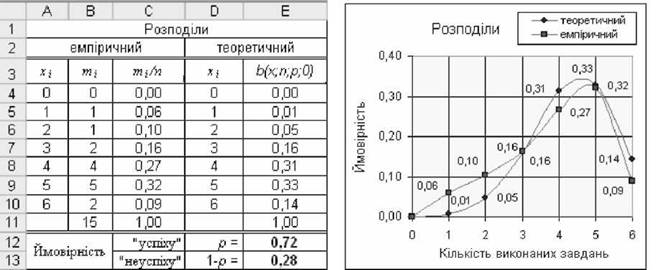
Рис. 3.41. Наближення теоретичного розподілу до емпіричного
Відповідь: ймовірність "успіху" складає приблизно 72% (р = 0,72) і більш ніж удвічі перевищує ймовірність протилежних наслідків (1-р) = 0,28. У змістовному плані це може означати, що, по-перше, результати тестування з більшою ймовірністю можна приймати за наслідок спроможності студентів до успішного виконання завдань, по-друге, - процедура іспиту має певний рівень діагностичних властивостей щодо навчальних досягнень студентів.
Розподіли "хі-квадрат", Стьюдента і Фішера
4. СТАТИСТИЧНЕ ОЦІНЮВАННЯ
Поняття статистичного оцінювання параметрів
Точкове оцінювання. Властивості статистичних оцінок
Методи статистичного оцінювання параметрів
Метод моментів
Метод максимальної правдоподібності
Метод найменших квадратів
Інтервальне оцінювання