Математична статистика - Руденко В.М. - Дисперсійний двофакторний аналіз

Дисперсійний двофакторний аналіз застосовується в тих випадках, коли досліджується одночасна дія двох факторів на різні вибірки об'єктів, тобто коли різні вибірки опиняються під впливом різних поєднань двох факторів. Може статися, що одна змінна значущо діє на досліджувану ознаку тільки при певних значеннях іншої змінної. Наприклад, посилення мотивації може підвищувати швидкість рішення завдань у високоінтелектуальних осіб і знижувати її у низькоінтелектуальних. Отже, дисперсійний двофакторний аналіз дозволяє оцінити не лише вплив кожного з факторів, але й їхню взаємодію.

Суть методу залишається тією самою, як і при однофакторній моделі, але у двофакторному дисперсійному аналізі можна перевірити більшу кількість гіпотез, проте розрахунки дещо складніші, ніж в однофакторних комплексах.

Дисперсійний двофакторний аналіз пред'являє особливі вимоги до формування комплексів. Для кожного фактора має бути не менше двох градацій; у кожному осередку комплексу повинно бути не менше двох спостережуваних значень для виявлення взаємодії градацій; комплекс має бути симетричною системою: кожній градації фактора А повинна відповідати однакова кількість градацій фактора В; результативна ознака повинна мати нормальний розподіл; фактори мають бути незалежними, що може бути підтверджено відсутністю кореляційного зв'язку між змінними-чинниками.

Приклад 6.2. Чотирьом групам по 4 випробовуваних у різних комбінаціях швидкості пред'явленні і довжини слова було запропоновано завдання з 10 слів для відтворення їх через деякий час (табл. 6.2).

Таблиця 6.2

Необхідно довести значущість припущення про те, що між факторами довжини слова (А) і швидкістю їх пред'явлення (В) спостерігається взаємодія: при великій швидкості пред'явлення краще запам'ятовуються короткі, при низькій швидкості - довгі слова, що показано на рис. 6.7.

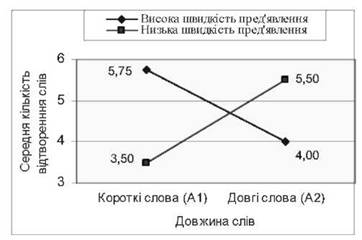
Рис. 6.7. Залежність середньої кількості відтворених слів від їхньої довжини і швидкості пред'явлення

Послідовність рішення:

o Формулювання гіпотез. Зважаючи на умови дослідження, необхідно висунути три комплекти неспрямованих гіпотез, які стосуються впливу фактора А окремо від фактора В, впливу фактора В окремо від фактора А і гіпотези про вплив взаємодії градацій факторів А і В.

Кількість відтворених слів різної довжини і швидкості їх пред'явлення

1-й комплект гіпотез:

Н₀(₁₎: відмінності в обсязі відтворення слів, обумовлені дією фактора А, є не більше вираженими, ніж випадкові відмінності між показниками;

Над: відмінності в обсязі відтворення слів, обумовлені дією фактора А, є більш вираженими, ніж випадкові відмінності між показниками.

2-й комплект гіпотез:

Н₀(₂/: відмінності в обсязі відтворення слів, обумовлені дією фактора В, є не більше вираженими, ніж випадкові відмінності між показниками;

Н₁(₂у відмінності в обсязі відтворення слів, обумовлені дією фактора В, є більш вираженими, ніж випадкові відмінності між показниками.

3-й комплект гіпотез:

Н₀(₃/: вплив фактора А на обсяг відтворення слів однаковий при різних градаціях фактора В і навпаки;

Н₁(₃₎: вплив фактора А на обсяг відтворення слів різний при різних градаціях фактора В і навпаки.

o Перевірка припущень: досліджуваний параметр має нормальний розподіл; вибірки незв'язані однакових обсягів; виміри за шкалою відношень.

o Визначення емпіричного критерію. Ситуації відповідає модель двобічного ^-критерію, для якого необхідно визначати три емпіричні значення:

¥_А - характеризує варіативність ознаки, зумовлену дією фактора А; ¥_в - характеризує варіативність ознаки, зумовлену дією фактора В; ¥_ЛВ - характеризує варіативність, зумовлену взаємодією факторів Л і В.

o Введені позначення:

п = 4 - кількість об'єктів (рядків у групі випробувань);

І = 2 - кількість факторів Л;

т = 2 - кількість факторів В;

піт = 2-2-4 = 16 - загальна кількість значень;

к- індекс об'єктів змінюється від 1 до п (і = 1, ..п);

і - індекс факторів Л змінюється від 1 до і (7 =

7 - індекс факторів В змінюється від 1 до т (к = 1,..т).

o Розрахунки критеріїв F_A , F_B і Fas рекомендовано починати з побудови за емпіричними даними спеціальної таблиці, що відтворює двофакторний дисперсійний комплекс (рис.6.8 і 6.9)

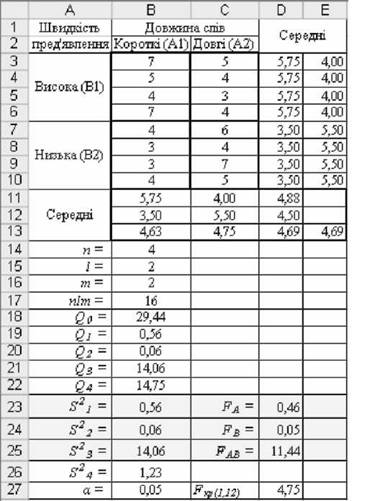
Рис. 6.8. Результати двофакторного дисперсійного аналізу

o Розрахувати середні значення :

у комірках В11:С12 для кожної вибірки

- 1 ^ - 1

^хі=-2^^хік (наприклад, хп =-(7 + 5 + 4 + 7) = 5,75); п к=1 4

у комірках Б3:Е10 повторити значення для кожної вибірки;

у комірках В 13:С 13 по фактору А (по стовпчику)

- 1 ¹ - 1

х*/ = -^х_ІІ (наприклад, х*1 = ~(5,75 + 3,50) = 4,63);

¹ і=1 ²

у комірках 011:012 по фактору В (по рядках)

хі* = - У х (наприклад, х1* = --(5,75 + 4,00) = 4,88 );

т _і=1 ²

у комірках Б13:Е13 для всіх вибірок

х = у-(х = (5,75 + 4,00 + 3,50 + 5,50) * 4,69);

1' т ,₌1 і₌1 2 o 2

o Розрахувати суми квадратів різниць у комірках В18:В22 за допомогою формул і відповідних виразів(див. рис. 6.9):

o Розрахувати середні квадрати у комірках В23:В26 за допомогою формул і відповідних виразів:

¹ ~ (1 -1)^{; 2}~(т -1)^{; 3}~(1 - 1)(т -1)^{; 4}~ 1 ■ т ■ (п -1) ^.

o Розрахувати емпіричні критерії у комірках В23:В25:

Р_А - 4 = ⁰⁵⁶ - 0,46; Г_в - 4 - ^0,06 . 0,05; Е_М - І = ^14,06 . 11,44; ^А я₄² 1,23 ' ^в я₄² 1,23 ' ^АВ я² 1,23 ' '

o Критичні значення ¥-критерію можна отримати за допомогою функції =РРАСПОБР для прийнятого рівня значущості а і ступенів вільності. І/_А = (1-1)=(2-1)=1, <#В=(т-1)=(2-1)=1, с$_АВ =(1-1)(т-1)=1 сІ/₂=1-т-(п-1)=12. Отже, і відповідні критичні значення для Р_крА , Р_крВ , Р_крАВ також будуть однакові. На рівні значущості 0,05 критичне значення Р(₁₁₂) ~ 4,75.

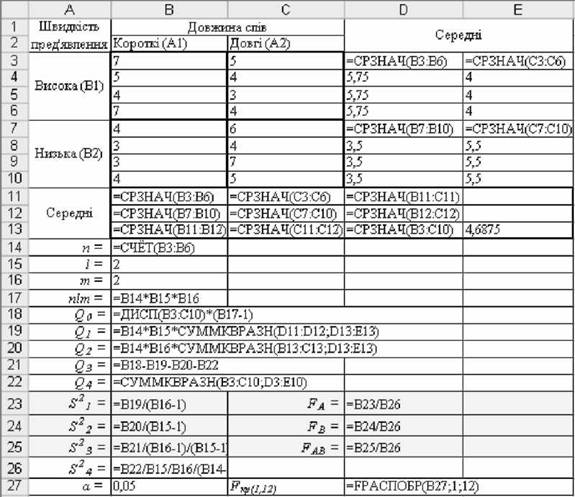
Рис. 6.9. Розрахункові формули двофакторного дисперсійного аналізу

o Прийняття рішення. Оскільки F_A < F(₁₁₂) (0,46 < 4,75) і F_B < F(₁₁₂) (0,05<4,75), нульові гіпотези И₀(і) і H₀(₂) приймаються. У той же час, оскільки Fab > F(ij₂) (11,44 > 4,75), нульова гіпотеза H₀(₃) відкидається .

o Формулювання висновків. Відмінності в обсязі відтворення слів, що обумовлені окремо факторами А і В, не є більш вираженими, ніж випадкові. Проте вплив фактора А на обсяг відтворення слів є різним при різних градаціях фактора В і навпаки. Висновки прийнято на рівні значущості 0,05.

Аналогічні результати можна отримати за допомогою пакета MS Excel "Аналіз даних" розділ "Двофакторний дисперсійний аналіз с повтореннями". Для цього у діалоговому вікні рис. 6.10 необхідно ввести відповідні параметри і отримати результати (рис. 6.11).

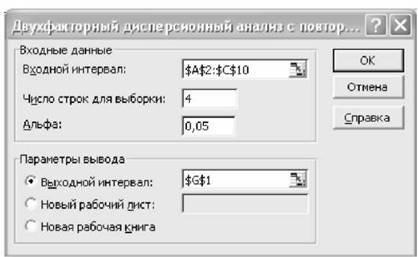
Рис. 6.10. Діалогове вікно двофакторного дисперсійного аналізу для незв'язаних вибірок

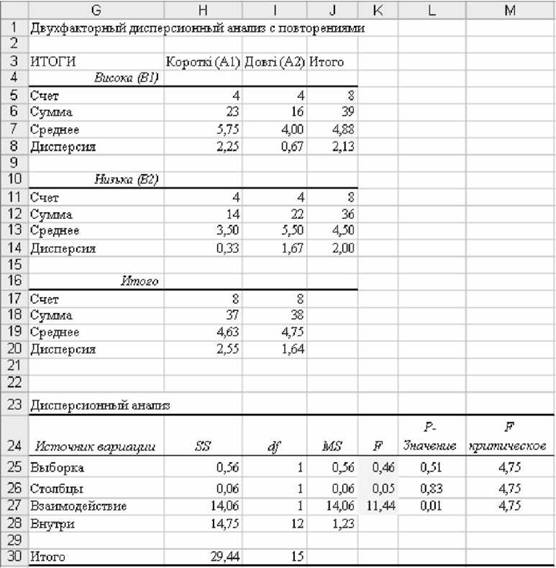
Рис. 6.11. Підсумки двофакторного дисперсійного аналізу

Отже, фактори довжини слів і швидкості їхнього пред'явлення окремо не впливають значуще на обсяг відтворення слів. Значущою виявляється взаємодія факторів: короткі слова краще запам'ятовуються при великій швидкості пред'явлення, а довгі - при повільній швидкості пред'явлення.

Пропонуємо самостійно розібратися з отриманими результатами, розрахунковими формулами та коментарем на рис. 6.7 - 6.11.

Запитання. Завдання.

1. Охарактеризуйте основні можливості методів дисперсійного аналізу.

2. Охарактеризуйте обмеження дисперсійного однофакторного аналізу.

3. Назвіть основу, на якій побудовано математичний апарат однофакторного дисперсійного аналізу.

4. Назвіть основу, на якій побудовано математичний апарат двофакторного дисперсійного аналізу.

5. Охарактеризуйте обмеження дисперсійного двофакторного аналізу.

6. Повторіть математичні процедури завдань за прикладами 6.1 - 6.2.

7. Виконайте лабораторні роботи № 23 і № 24.