Середню геометричну застосовують, коли загальний обсяг явища є не сума, а добуток значень ознаки. Ця середня використовується здебільшого для розрахунку середніх коефіцієнтів (темпів) зростання і приросту при вивченні динаміки явищ (див. розділ 10) і має такий вигляд:
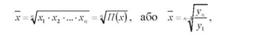
де п - число коефіцієнтів зростання; у і у - початковий і кінцевий рівні динамічного ряду.
Величина середньої геометричної залежить тільки від співвідношення кінцевого і початкового рівнів. Якби не змінювались в цих межах інші рівні, величина середньої не зміниться.
Розглянемо такий приклад. За даними про посівну площу цукрових буряків у господарстві за 5 років знайти середній коефіцієнт зростання площі посіву цукрових буряків за 2005 - 2009 рр. Всі розрахунки зведемо в табл. 4.5.
Таблиця 4.5. Дані для розрахунку середньої геометричної
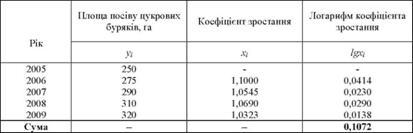
Середнє значення логарифма коефіцієнта зростання становитиме: 0,1072 : 4 = 0,0268. За таблицями антилогарифмів знайдемо середній коефіцієнт зростання посівної площі цукрових буряків: апіії%х = 1,0636, або 106,36%.
Такий саме результат одержимо і за другою формулою:

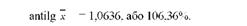
Отже, середній коефіцієнт зростання посівної площі цукрових буряків у господарстві за 2005 - 2009 рр. становив 1,0636. Інакше кажучи, посівна площа цукрових буряків у господарстві щорічно збільшувалась в середньому на 6,36%.
Середня квадратична
Середня квадратична використовується переважно для розрахунку показників варіації (коливання) ознаки - дисперсії і середнього квадратичного відхилення, які обчислюються на основі квадратів відхилень індивідуальних значень ознаки від їхньої середньої арифметичної. Крім того, вона застосовується для узагальнення ознак, виражених лінійними мірами яких-небудь площ (при обчисленні середніх діаметрів стовбурів дерев, кошиків, листків, клубнів тощо).
Формули її такі:
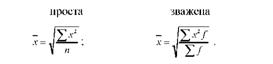
Наприклад, є дані про розмір діаметрів стовбурів трьох яблунь (хг): 17; 22; 19 см. Потрібно обчислити середній розмір діаметра стовбура яблуні. Оскільки вихідні дані представлені у вигляді квадратних функцій, середній розмір діаметра стовбура яблуні визначимо за формулою середньої квадратичної простої:
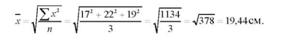
Якби у наведеному прикладі окремі значення діаметра стовбура повторювались неоднакове число разів, то середній розмір діаметра стовбура слід було б розраховувати за формулою середньої квадратичної зваженої.
Досліджуючи статистичну сукупність, можна виявити, що поряд з ознаками, які притаманні усім одиницям досліджуваного явища, є й такі ознаки, якими одні одиниці володіють, а інші ні. Такими ознаками, наприклад, будуть наявність в партії продукції бракованої продукції, рослини уражені хворобами та ін. Такі виключаючі один одного ознаки називають альтернативними. При альтернативній варіації, коли є лише два виключаючих один одного випадки, наявність ознаки у одиниці сукупності прийнято позначати 1, а її відсутність - 0. Частку одиниць, що володіють досліджуваною ознакою, позначають р, а долю одиниць, не вододіючих цією ознакою, - д. Очевидно, що р + д = 1, а д = 1 -р.
Середнє значення альтернативної ознаки, обчислене за формулою середньої арифметичної, буде дорівнювати:
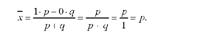
Отже, середнє значення альтернативної ознаки дорівнює частці одиниць сукупності, що володіють даною ознакою.
Якщо обчислити різні типи середніх величин, одержаних з степеневої середньої, для одного і того самого варіаційного ряду, то їх чисельні значення будуть відрізнятися один від одного, а самі середні розташуються таким чином:
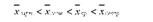
тобто найбільшою буде середня квадратична, а найменшою - середня гармонічна. Порядок зростання середніх визначається значенням степені к в степеневій середній.
Ця властивість степеневих середніх одержала назву властивості мажорантності середніх.
Приклад. Нехай маємо такі значення ж,: 2; 3; 36. Обчислимо вказані середні величини:

Одержані середні розташуються у такому порядку: 3,50 <6,00< 13,67< 20,89, що відповідає вимозі властивості мажорантності середніх:
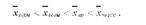
4.3. Властивості середньої арифметичної. Розрахунок середньої арифметичної способом моментів
4.4. Мода, медіана, квартілі і децилі
Розділ 5. Показники варіації
5.1. Поняття варіації ознак. Показники варіації
Розмах варіації
Абсолютні показники варіації
Відносні показники варіації
5.2. Математичні властивості дисперсії та спрощені способи її розрахунку
5.3. Види дисперсій і правило їх додавання