Теорія статистики - Мармоза А.Т. - 4.4. Мода, медіана, квартілі і децилі

Крім перелічених вище середніх у статистичному аналізі як узагальнюючі характеристики сукупності використовують такі значення ознаки, які відрізняються особливим розташуванням у варіаційному ряду розподілу. Це так звані структурні (позиційні) середні. Із них найчастіше застосовують моду і медіану.

Величина моди і медіани залежить лише від характеру частот, тобто від структури розподілу. Якщо величина середньої арифметичної залежить від усіх значень ознаки, то величина моди і медіани не залежить від крайніх значень ознаки. Це особливо важливо для рядів розподілу, в яких крайні значення ознаки мають нечітко виражені межі (до і понад).

Модою називають значення ознаки, що має найбільшу частоту в статистичному ряду розподілу. Спосіб обчислення моди залежить від того, в якому вигляді дано значення ознаки: дискретного чи інтервального ряду розподілу. В дискретних варіаційних рядах моду обчислюють без додаткових розрахунків за значенням варіанти з найбільшою частотою. Наприклад, відомий змінний виробіток деталей робітниками цеху:

виробіток деталей, шт 30 33 35 38

число робітників, чол. 7 10 15 12

В даному прикладі модальною величиною є 35 деталей, так як ця величина у досліджуваній сукупності має найбільшу частоту - 15 випадків. Модальною ціною на той або інший продукт на ринку є та ціна, яка спостерігається найчастіше.

При розрахунку моди в інтервальному варіаційному ряду розподілу спочатку потрібно визначити модальний інтервал, в межах якого знаходяться мода, а потім значення модальної величини ознаки.

В інтервальному варіаційному ряду розподілу модою наближенно вважають центральний вараінт так званого модального інтервалу, тобто того інтервалу, який має найбільшу частоту. В межах інтервалу необхідно знайти те значення ознаки, яке є модою.

В інтервальних варіаційних рядах розподілу моду визначають за формулою:

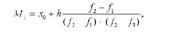
де х0 - нижня (мінімальна) межа модального інтервалу; к - величина інтервалу; /1 - частота передмодального інтервалу; /2 - частота модального інтервалу; /3 - частота післямодального інтервалу.

Формула ґрунтується на припущенні, що відстані від нижньої межі модального інтервалу до моди і від моди до верхньої межі модального інтервалу прямо пропорційні різницям між чисельностями (частотами) модального інтервалу і інтервалів, що прилягають до нього.

Розрахунок моди в інтервальному варіаційному ряду розподілу покажемо на прикладі розподілу 100 господарств за надоєм молока на корову (табл. 4.8).

Таблиця 4.8. Дані для розрахунку моди і медіани в інтервальному ряду розподілу

Інтервал, в якому міститься мода, буде 32 - 34 ц, так як цей інтервал найбільшу частоту.

Підставивши відповідні числові значення у формулу моди, одержимо:

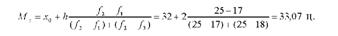
Отже, у досліджуваній сукупності найбільше число господарств має продуктивність корів 33,07 ц.

Мода і середня величина по-різному характеризують сукупність. Мода визначає безпосередньо розмір ознаки, притаманної хоча і значній частині сукупності, але ж не всій сукупності. Мода за своїм узагальнюючим значенням менш точна порівняно з середньою арифметичною, яка характеризує сукупність в цілому з урахуванням усіх без винятку елементів сукупності.

Медіаною називають таке значення ознаки, яке поділяє ранжирований ряд розподілу на дві рівні частини, тобто значення, яке перебуває в середині ряду розподілу. Якщо в дискретному варіаційному ряду 2т + 1 випадків, то значення ознаки у випадку т + 1 є медіанним. Якщо в ряду парне число 2т випадків, медіану визначають як середню арифметичну з двох середенних значень. Наприклад, якщо 15 комбайнерів агрофірми розташувати у порядку зростання, тобто в ранжирований ряд за кількістю намолоченого ними зерна, то намолот зерна у восьмого комбайнера буде медіанним. Якщо ж число комбайнерів буде 16 чоловік, то медіаною буде середнє значення намолота зерна восьмого і дев'ятого комбайнерів.

Медіану з парним і непарним числом варіант у дискретному ряду розподілу обчислюють за формулами:

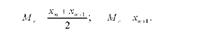
В інтервальному варіаційному ряду розподілу медіану визначають за формулою:

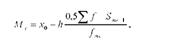
де х 0 - нижня (мінімальна) межа медіанного інтервалу; к - величина інтервалу; 0,5^ ї - половина суми нагромаджених частот інтервального ряду розподілу; 3т,-1 - сума нагромаджених частот інтервалу, що передує медіанному; /т, - частота медіанного інтервалу.

Для визначення медіани в інтервальному варіаційному ряду розподілу треба обчислити нагромаджені частоти і відшукати медіанний інтервал. Під нагромадженими частотами розуміють наростаючий підсумок частот, починаючи з першого інтервалу. Медіанним є той інтервал, на який припадає перша нагромаджена частота, що перевищує половину всього обсягу сукупності.

Обчислимо медіану за даними цього самого інтервального ряду розподілу (табл. 4.8). За даними таблиці побудуємо ряд нагромаджених частот і знайдемо медіанний інтервал. Медіанним інтервалом є інтервал 32 - 34 ц, так як на цей інтервал припадає перша нагромаджена частота, що перевищує половину всього обсягу сукупності (66 перевищує £/ : 2 = 100:2= 50).

Медіанне значення продуктивності корів становитиме:

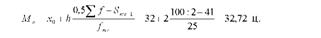
Отже, продуктивність корів, рівна 32,72 ц і є варіантою, що поділяє варіаційний ряд розподілу 100 господарств на дві рівні частини (50 господарств має надій на корову менше 32,72 ц і 50 господарств - більше 32,72 ц).

Мода і медіана, як правило, відрізняються від значення середньої, збігаючись з нею тільки у випадку симетричного розподілу частот варіаційного ряду: х = M0 = Me. Тому співвідношення моди, медіани і середньої арифметичної дає змогу оцінити асиметрію ряду розподілу (див. розд. 5).

Для помірно асиметричних розподілів К.Пірсон встановив таке наближене співвідношення між цими характеристиками:

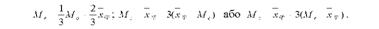
Медіана є кращою характеристикою центральної тенденції, коли межі крайніх інтервалів відкриті. Медіана є найприйнятнішою характеристикою і в разі, якщо в ряду розподілу є значно великі і значно малі значення, які впливають на середню величину, а на медіану - ні. Медіана, крім того, володіє властивістю лінійного мінімуму: сума абсолютних значень відхилень величини ознаки у всіх одиниць сукупності від медіани, найменша, тобто

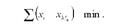
Ця властивість має велике значення для вирішення деяких практичних завдань - наприклад, для розрахунку самої короткої з усіх можливих відстаней

для різних видів транспорту, для розміщення станцій технічного обслуговування таким чином, щоб відстань до всіх машин, що обслуговуються даною станцією, була мінімальною і т. п.

Моду і медіану застосовують звичайно в тих випадках, коли визначати середню арифметичну недоцільно. Так, немає сенсу обчислювати середній розмір одягу і взуття, що їх виробляють фабрики. Для цього досить знати модальні розміри одягу і взуття, тобто ті, які користуються найбільшим попитом у населення з тим, щоб фабрики, плануючи своє виробництво, могли якомога краще задовольнити попит покупців саме на ці розміри одягу і взуття.

Медіана широко використовується при проектуванні місць будівництва об'єктів масового обслуговування населення (шкільних та дошкільних закладів, кінотеатрів, підприємств служби побуту і торгівлі тощо). Наприклад, продовольчий магазин у сільському селищі доцільно розташувати в такій точці, щоб він обслуговував половину кількості мешканців селища, а не розташовувався точно в середині його.

Додатково до медіани для характеристики структури варіаційного ряду розподілу обчислюють квартилі, які поділяють ранжирований ряд на 4 рівні частини, і децилі, які поділяють ранжирований ряд на 10 рівних частин. Другий квартиль 22 - дорівнює медіані, а перший - <21 і третій - 23 обчислюють аналогічно розрахунку медіані, тільки замість медіанного інтервалу беруть для першого квартиля інтервал, в якому знаходиться варіанта, що відокремлює 1/4 кількості частот, а для третього квартиля - інтервал, в якому знаходиться варіанта, що відокремлює 3/4 кількості частот.

В інтервальному ряду розподілу перший і третій квартиль розраховують за такими формулами:

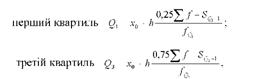
де х0 - нижні (мінімальні) межі квартальних інтервалів; к - величина інтервалу; £ / - сума нагромаджених частот ряду розподілу; 5а 1 і 5а 1 - нагромаджені частоти інтервалу, що передує інтервальному відповідно для першого і третього кварталів; /аі /& - частоти квартальних інтервалів.

Розрахунок першого і третього кварталів розглянемо на прикладі табл. 4.8.

Обчислимо перший квартиль. Для знаходження інтервалу, в якому знаходиться перший квартиль, використаємо нагромаджені частоти. Перший квартиль знаходиться в інтервалі, в який входить перша нагромаджена частота, що перевищує чверть загального обсягу сукупності (0,25 100 = 25). Отже, перший квартиль (1 знаходиться в третьому інтервалі (з надоєм молока від 30 до 32 ц), який має суму нагромаджених частот 41.

Значення першого квартиля:

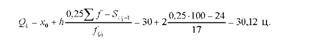
Це означає, що одна чверть господарств має надій 30,12 ц, а три чверті - більше як 30,12 ц.

Щоб визначити третій квартиль, знайдемо інтервал, в якому він знаходиться. На цей інтервал припадає перша нагромаджена частота, що перевищує три чверті загального обсягу сукупності (0,75 ■ 100 = 75). Отже, третій квартиль знаходиться в інтервалі 34 - 36 ц, який має суму нагромаджених частот, рівну 84.

Значення третього квартиля:

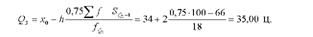
Отже, три чверті господарств мають надій молока на корову до 35,00 ц, а одна чверть - більше як 35,00 ц.

В інтервальному ряду розподілу децилі визначають за такою формулою:

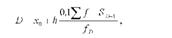
де х0 - нижня (мінімальна) межа відповідного децильного інтервалу; к - величина інтервалу; - сума нагромаджених частот інтервалів, що передують децильним; Фв - частоти відповідних децильних інтервалів.

Підставивши дані табл. 4.8 у формулу, визначимо перший деціль:

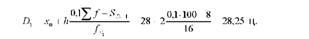
Отже, десята частина всіх господарств має надій на корову 28,25 ц і менше, а решта (90%) - більше як 28,25 ц.

Аналогічно розраховуються і решта децилів (другий, третій і т.д.).