Розробку теорії портфеля першим розпочав в 50-х роках XX ст. П. Марковіц. Основним результатом започаткованої ним теорії стала розробка основних принципів побудови ефективного портфеля, а саме такого, який максимізу с очікуваний дохід при задовільному ступені ризику.
При розробці теорії портфеля П. Марковіцем було зроблено низку припущень щодо поведінки інвестора та параметрів портфеля. Так, інвестор вважається несхильними до ризику. Якщо існує два варіанти однанового доходу, але різного ступеня ризику, інвестор обирає варіант з меншим ризиком. Портфель цінних паперів інвестор формує лише з ризикових активів, майбутній дохід за якими наперед невизначений. Розподіл імовірностей для портфеля цінних паперів є нормальним.
Визначення дохідності та ризиковості портфеля здійснюється протягом одного часового періоду, як правило, року. Оцінки, отримані для такого періоду, не можуть бути узагальнені на більш тривалий період часу, оскільки невизначеність, пов'язана з часом, та невизначеність і випадковий характер цінових змін на ринку збільшують невизначеність прогнозів, що стосуються майбутніх змін в ризиковості та дохідності портфеля.
Побудова ефективного портфеля за П. Марковіцем ґрунтується на тому, що інвестор формує портфель тільки з ризикових активів. Для визначеного ступеня ризику існує множина портфелів з різним рівнем очікуваного доходу, причому для кожного ступеня ризику існує своя множина портфелів. Допустиму множину всіх таких портфелів (область обмежена лініями І— ІІ—III) наведено нарис. 8.3. Точки, розміщені на вертикальних відрізках, що належать допустимій області, характеризують множину портфелів, які мають однаковий рівень ризику, але різний рівень очікуваного доходу. Точки, що належать кривій II—ІІІ, відображають множину ефективних портфелів, які характеризуються різним рівнем ризику і максимальним для цього рівня ризику доходом.
Оптимальним для інвестора портфелем буде найбільш прийнятний із множини усіх ефективних портфелів. Вибір з множини ефективних портфелів оптимального залежить від схильності інвестора до ризику. Чим вищий рівень ризику вважає для себе прийнятним інвестор, тим вищий рівень доходу забезпечить йому оптимальний портфель.
Вибір оптимального з максимальним доходом портфеля здійснюється методами квадратичного програмування.
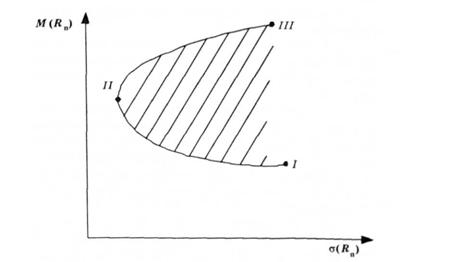
Рис. 8.3. Допустима множина портфелів
Чим менша кореляція між активами портфеля, тим більшою може бути максимальна дохідність портфеля при заданому рівні ризику.
Формування ефективного портфеля як з ризикових, так і з безризикових активів передбачає теорія ринку капіталів* Відповідно до цієї теорії всі інвестори формують інвестиційні портфелі з певних часток безризикових цінних паперів та ринкового портфеля. Основні припущення теорії щодо ринку та поведінки інвесторів на ньому полягають у тому, що:
* інвестори прагнуть уникнути ризику; якщо ризику не можна уникнути, він повинен компенсуватися можливістю отримати більшу ставку доходу як премію за ризик;
* кожний інвестор прагне сформувати портфель з протилежно корельованих цінних паперів з тим, щоб підвищити ефективність диверсифікації портфеля;
* усі інвестори на ринку приймають рішення щодо інвестицій протягом одного періоду (одним періодом можна вважати будь-який період: півроку, рік, кілька років);
* передбачається нормальний розподіл імовірностей майбутнього доходу;
* усі учасники ринку мають однакові очікування щодо побудови інвестиційного портфеля, а саме всі вони мають намір сформувати ефективний, за П. Марковіцем портфель;
* ринок є ефективним конкурентним ринком, окремі інвестори не можуть вплинути на ринкову вартість активів, ринкові ціни встановлюються на основі врівноваження попиту та пропозиції на відповідні активи;
* не враховуються витрати обігу — додаткові кошти, що витрачаються при купівлі-продажу цінних паперів на ринку;
* інвестори можуть інвестувати і залучати кошти під одну й таку саму безризикову процентну ставку.
Відповідно до теорії ринку капіталів інвестор формує портфель з ризикових та безризикових цінних паперів. Безризиковий цінний папір має визначену дохідність протягом одного періоду і стандартне відхилення, що дорівнює 0 (Q6= 0). Безризиковий цінний папір не корелюється з цінними паперами, що входять до множини ефективних портфелів, тобто, має коефіцієнт кореляції, що дорівнює О(соr (R6,Rp ) = 0). Величина частки безризикових активів у портфелі залежить від того, якою мірою інвестор уникає ризику, тобто який рівень ризику він вважає для себе допустимим.
Припустимо, що інвестор формує портфель, що складається з ω6 безризикових і ω = 1 - ω 6 ризикових цінних паперів з множини ефективних за П. Марковіцем. Позначимо на вертикальній осі (рис. 8.4) точку що відображає дохідність безризикового активу (безризикову процентну ставку). З цієї точки проведемо дотичну до лінії II—III, що відображає множину ефективних портфелів (див. рис. 8.3). Дотична відображає множину портфелів, що складаються з певної частки безризикових активів та ринкового портфеля, і називається лінією ринку капіталів {ЛРК),
Усі портфелі, що розміщені націй лінії, є досяжними (реальними) для інвестора. Чим більша частка без
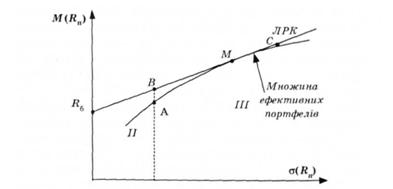
Рис. 8.4. Лінія ринку капіталів
ризикових активів у сформованому портфелі, тим ближче точка на ЛРК до точки Я6 на вертикальної осі. Точка М, що е точкою дотику ЛРК до межі множини ефективних портфелів, характеризує ринковий портфель, що складається з усіх ризикових активів, які перебувають в обігу на ринку. Причому частка певного виду активу в портфелі пропорційна до сумарної ринкової вартості всіх активів цього виду. Це означає, що акції великої компанії становлять більшу частку портфеля, ніж акції меншої корпорації.
Множина всіх рівноважних портфелів розміщена на ЛРК. Чим більше інвестор уникає ризику, тим ближче буде сформований ним портфель до точки R6. Точки, розміщені ліворуч точки М, відображують інвестиційні портфелі, що є комбінацією безризикових та ризикових активів. Точки, розміщені праворуч точки М відображують портфелі, що містять лише ризикові активи, одна частина яких придбана за власні кошти, а інша — за рахунок залучених під безризикову процентну ставку. Причому якщо частина залучених коштів дорівнює за величиною ω6, частина власних коштів має дорівнювати 1 + ω6. Наприклад, для точки С це означає залучення коштів у розмірі ω6 = - 0,5 і вкладення їх в ринковий портфель, тобто ωр = 1 - ω6 = 1,5. За наявності 10 000 гр. од. залучаються 5000 гр. од. і вкладаються всі 15 000 гр. од. в ринковий портфель.
На відрізку R6М будь-який із портфелів формується з певної частки безризикових активів і ринкового портфеля. Тобто кошти інвестуються під безризикову процентну ставку та в ринковий портфель. Конкретні цінні папери розміщені нижче від ЛРК. Цінні папери, що мають коефіцієнт кореляції з ринком, який дорівнює 1, розміщені на ЛРК. їх використання для диверсифі-кованого портфеля не може дати позитивного ефекту.
Портфель з множини ефективних портфелів, якому відповідає точка А, та портфель на ЛРК, якому відповідає точка В, мають однаковий ступінь ризику, проте різну дохідність. Портфель, що є комбінацією безризикових та ризикових активів (точка В), має вищу дохідність. Інвестор, що ухиляється від ризику, звичайно, віддасть перевагу портфелю В.
Отже, якщо вважати, що інвестор формує портфель не тільки з ризикових, а й з безризикових активів, допустимою множиною таких портфелів, які задовольняють різним рівням ризику, є лінія Я^М, або лінія ринку капіталів. Точкам цієї лінії відповідають портфелі, що є комбінацією залучених або інвестованих під безризикову процентну ставку коштів та портфеля ризикових активів. Оптимальним для інвестора портфелем буде портфель Q(Rn), який задовольняє вимогам інвестора щодо допустимих рівнів ризику за портфелем. Рівняння лінії ринку капіталів має вигляд

Після підстановки цього виразу в рівняння (8.4) рівняння лінії ринку капіталів матиме вигляд
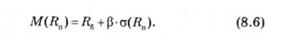
Отже, відповідно до теорії ринку капіталів очікуваний дохід за портфелем дорівнює безризиковій процентній ставці та премії за ризик, яка дорівнює добутку ринкової ціни ризику на стандартне відхилення а(Лп), що кількісно відображує ризик за портфелем.
Практикум
Розділ 9. УПРАВЛІННЯ КАПІТАЛОМ
9.1. Оцінка капіталу
9.2. Вартість капіталу
9.3. Визначення вартості позикового капіталу
9.4. Визначення вартості власного капіталу
Вартість акціонерного капіталу
Вартість джерела "нерозподілений прибуток"
9.5. Середньозважена та гранична вартість капіталу