Фінансовий менеджмент - Шелудько В.М. - 8.5. Модель оцінки капітальних активів

Модель оцінки капітальних активів (MOKA) є дво-параметричною моделлю, яка розглядає взаємозв'язок двох основних характеристик цінного папера — доходу та ризику. Ґрунтуючись на результатах теорії ринку капіталів, модель дає змогу оцінити необхідну ставку доходу за будь-яким цінним папером на основі систематичного ризику та безризикової процентної ставки.

MOKA пов'язує оцінку цінних паперів з процесом диверсифікації. Згідно з MOKA ризиковість окремого цінного папера характеризує не стандартне відхилення, яке відображає всю сукупність ризиків, а лише ризик, що залишається після диверсифікації. Саме цей ризик має особливе значення для інвестора, оскільки не може бути ліквідованим через включення цінного папера до диверсифікованого портфеля. Його називають чистим ризиком. Він характеризується коефіцієнтом Я, що відображає чутливість цінного папера до змін ринкової дохідності. Коефіцієнт β відображає чистий ризик за цінним папером, який не може бути зменшений через диверсифікацію.

Як систематичний ризик, що характеризується коефіцієнтом β, так і несистематичний можуть бути кількісно оцінені. Оскільки систематична складова доходу за цінним папером пропорційна до ринкової дохідності, вона може бути подана у вигляді βRp. Несистематичну складову, яка не залежить від ринкової дохідності, позначимо величиною ε0. Величину несистематичної складової можна подати у вигляді ε0 = а + ε, де середнє

значення ε => 0 . Тоді очікуваний рівень доходу за цінним папером, або необхідна ставка доходу, визначається сумою:

Якщо коефіцієнт β цінного папера більший за 1, при зростанні ринкових процентних ставок на деяку величину його дохідність зросте ще більшою мірою. При падінні ринкової дохідності дохідність цього цінного папера буде падати ще стрімкіше. Якщо, наприклад, β = 1,5, тоді ринкова дохідність на рівні 10 % збільшить рівень доходу за даним цінним папером до 15 %.

Для виявлення характеру взаємозв'язку між дохідністю окремого цінного папера та ринковою дохідністю використовують регресійний аналіз. На рис. 8.5 точками показано залежність між ринковою дохідністю Rр, що може відображатись одним з ринкових індексів, та дохідністю акцій деякої корпорації А. За допомогою методу найменших квадратів будують пряму, яка мінімізує суму квадратичних відхилень точок від прямої. Величина є характеризує віддаль від точок до прямої, а — довжина відрізку, що відтинає пряма на вертикальній осі. Коефіцієнт Р — тангенс кута нахилу пря

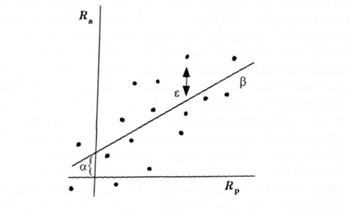
Рис. 8.5. Залежність між дохідністю акції корпорації та ринковою дохідністю мої. Він характеризує чутливість акцій А до змін ринкової дохідності. Якщо β = 1 (кут нахилу дорівнює 45º), зміни в дохідності акції корпорації А дорівнюють змінам ринкової дохідності. Якщо, наприклад, середній рівень доходу на ринку зріс на 0,5 %, рівень доходу за акціями А також збільшиться на 0,5 %.

Для акцій зі значним коефіцієнтом р, що дуже чутливі до змін в економіці, значну частину ризику становить систематичний ризик, який не може бути зменшений через диверсифікацію. Для таких акцій диверсифікація не приводить до значних змін в їх ризиковості. Для акцій з низьким значенням р диверсифікація значно зменшує загальний ризик за акцією, оскільки більшу її частину становить несистематичний ризик.

Систематичний ризик за цінним папером пропорційний до ринкового ризику, що характеризується σ(Rр), з коефіцієнтом пропорційності β, тобто дорівнює βσ(Rр). Несистематичний ризик характеризується стандартним відхиленням величини ε0, тобто (ε0).

Систематичний ризик портфеля цінних паперів рп визначають через систематичні ризики р, цінних паперів, що входять до портфеля:

де ωi — частка j-го цінного папера, що міститься в портфелі.

Якщо портфель містить всі ринкові цінні папери з відповідними вагами ωi коефіцієнт βn буде дорівнювати 1, оскільки це буде ринковий портфель.

Несистематичний ризик за портфелем також виражається через несистематичний ризик окремих цінних паперів, проте в процесі диверсифікації ця величина прямує до нуля. Коефіцієнт β можна назвати відносним показником ризику, оскільки він відображає систематичний ризик цінного папера або портфеля відносно ринкового ризику, який може бути розрахований як стандартне відхилення для ринкового портфеля.

Для акцій, що котируються на Нью-Йоркській фондовій біржі, систематичний ризик становить до 30 %

загального ризику, а несистематичний — 70 %. Для добре диверсифікованого портфеля несистематичний ризик — до 10 % загального ризику, систематичний — до 90%.

Лінія на рис. 8.6 відображає залежність між очікуваним рівнем доходу та ризиком окремого цінного папера. Вона має назву лінії ринку цінних паперів (ЛРЦП), Відповідна аналітична залежність має вигляд

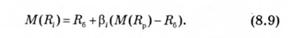
де М(Ri) — очікувана дохідність j-го цінного папера; R6 — дохідність безризикового цінного папера; М(Rp) — очікувана ринкова дохідність.

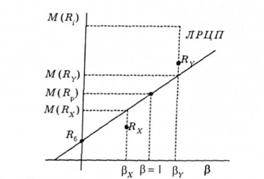
Рис. 8.6. Залежність між очікуваним доходом та ризиком окремого цінного папера

Чим більш ризиковий цінний папір, тим вищий його коефіцієнт р, а отже, тим вищий рівень доходу повинен він забезпечити.

При оцінці акцій коефіцієнт р, як і ринковий ризик, інвестори розраховують на основі даних за попередні місяці та роки. (Для багатьох компаній, акції яких перебувають в обігу на ринку, коефіцієнти р розраховують відомі інформаційні та рейтингові агентства.) За допомогою коефіцієнта р інвестори, користуючись ЛРЦП, визначають необхідну ставку доходу, яку мають забезпечити акції відповідної компанії. Порівнюючи отриману ставку доходу з дохідністю, яку реально пропонує корпорація, вони роблять висновки про те, недооцінені чи переоцінені такі акції ринком.

Припустимо, що βх, βv— коефіцієнти для корпорацій X, Y. Rx, Ry — дохідність акцій X та Y відповідно (див. рис. 8.6). Акції корпорації X вважаються переоціненими, оскільки вони забезпечують дохідність на рівні Rx, що нижче від необхідної ставки доходу M(RX), яка відповідає ступеню ризику акцій X. Акції, що мають коефіцієнт Рх> мають забезпечити згідно з MOKA дохідність на рівні М(Rx). Так само акції Y можна вважати недооціненими, оскільки вони забезпечують рівень доходу Лу, що вище від необхідної ставки доходу M(Ry)f яка відповідає ступеню ризику βу.

Очікувану дохідність окремого цінного папера можна виразити через ринкову дохідність та безризикову процентну ставку аналогічно очікуваній дохідності портфеля (8.4):

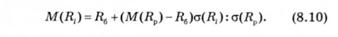
Враховуючи формулу (8.7) і те, що в диверсифікованому портфелі несистематичний ризик зменшується до нуля, можна записати:

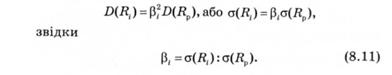
Підставивши залежність у рівняння (8.10), отримаємо

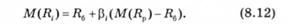
Отже, на основі MOKA очікувану дохідність акції чи іншого цінного папера визначають безризикові процентні ставки, коефіцієнт чутливості р до ринку та середня ринкова дохідність. Причому коефіцієнт р характеризується співвідношенням (8,11) ризику окремого цінного папера до середньоринкового ризику.

Як і інші методи оцінки акцій, модель оцінки капітальних активів має як переваги, так і недоліки. До переваг MOKA можна віднести глибоке дослідження та послідовне використання ризику і його впливу на очікувану дохідність акцій. Недоліками методу є його одноперіодичність та велика кількість припущень щодо поведінки інвесторів.