Математична статистика - Руденко В.М. - Критерії асиметрії та ексцесу

При використанні методів математичної статистики надзвичайно важливо знати закон розподілу властивості, що вивчається. По суті, вже сама досліджувана змінна представлена масивом емпіричних даних з певним законом розподілу ймовірностей реалізації її значень. Тому будь-яка статистична обробка починається, як правило, зі спроби оцінити закон розподілу. Прагнення застосувати методи, які розроблено для певного закону розподілу, в умовах, коли реальний розподіл відрізняється від гіпотетичного, є найбільш розповсюдженою помилкою, що призводить у підсумку і до помилкових висновків.

Критерії перевірки гіпотез щодо закону розподілу прийнято називати критеріями згоди, які можна розділити на дві групи: загальні та спеціальні [37, С. 20]. Загальні критерії застосовують до формулювань гіпотез про згоду спостережень з будь-яким можливим розподілом. Спеціальні критерії згоди використовують у разі перевірки гіпотези щодо конкретної форми розподілу - нормальної, рівномірної, експоненціальної тощо. Такі критерії носять відповідну назву - критерії нормальності, критерії рівномірності й т.п.

Розрахунки емпіричного розподілу та його графічна візуалізація не дають надійних підстав для висновку щодо закону розподілу ознаки у сукупності, з якої взята вибірка. Тим часом знання цього закону є необхідною умовою використання багатьох математичних методів. Наприклад, застосування параметричних критеріїв, дисперсійного аналізу вимагає попередньої перевірки нормальності розподілу досліджуваної ознаки.

Серед методів оцінювання законів розподілу ймовірностей випадкових величин біля двох десятків було спеціально розроблено для перевірки нормальності. Найбільш розповсюдженими вважаються критерії асиметрії й ексцесу, хі-квадрат та ін. Проте варто рекомендувати критерій Шапіро-Вілка У¥, який за рейтингом потужності посідає перше місце [37, С 278]. Розглянемо методику, техніку й особливості використання трьох критеріїв: асиметрії й ексцесу, хі-квадрат і Шапіро-Вілка. Причому для порівняння будемо використовувати у навчальних прикладах одні й ті самі емпіричні дані.

Критерії асиметрії та ексцесу

Критерії асиметрії та ексцесу застосовують для приблизної перевірки гіпотези про нормальність емпіричного розподілу. Асиметрія характеризує ступінь несиметричності, ексцес - ступінь загостреності (згладженості) кривої диференціальної функції емпіричного розподілу в порівнянні з функцією щільності нормального розподілу.

Для нормального розподілу N(¿1,0) з математичним сподіванням /г і дисперсією а¹ третій і четвертий центральні моменти мають сенс асиметрії і ексцесу. Відповідні коефіцієнти А і Е дорівнюють нулю:

Отже, нормальний розподіл є симетричний відносно середнього значення і є "ідеальний" - не загострений і не згладжений.

Дисперсії асиметрії та ексцесу відповідно дорівнюють

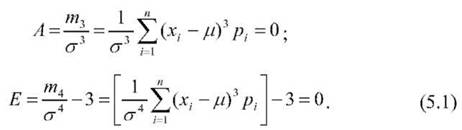
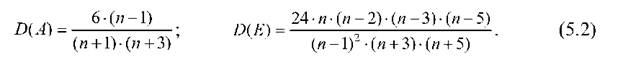
Вважається, що при нормальному розподілі вибіркові показники асиметрії та ексцесу дорівнюватимуть нулю, але реально таке майже не спостерігається. Тому емпіричний розподіл вважають близьким до нормального (приймають нульову гіпотезу), якщо виконуються умови:

|4x| * 3ЩА) і К| ^ 5л/ОД . (5.3)

Технологічно у цьому методі розраховують показники t_A і t_E

Про достовірну відмінність емпіричного розподілу від нормального свідчать показники t_A і t_E, якщо приймають значення 3 і більше.

Приклад 5.2. Перевірити відповідність розподілу емпіричних вибіркових даних (стовпчики А:В рис. 5.4) нормальному законові розподілу ознаки.

Послідовність рішення.

o Формулювання гіпотез:

H₀: емпіричний розподіл не відрізняється від нормального; H₁: емпіричний розподіл відрізняється від нормального.

o Вибір статистичного критерію. Для перевірки статистичних гіпотез використаємо метод критеріїв асиметрії та ексцесу з розрахунком t_A і t_E:

A I |E_x|

^іа = ^ і ^ = , (5.5)

де A_x і E_x - емпіричні коефіцієнти асиметрії та ексцесу; m_A і m_E дорівнюють: m I ⁶-(ⁿ-¹⁾ ; m_E - p4-ⁿ-⁽ⁿ-²Hⁿ-³HⁿEI. (5.6)

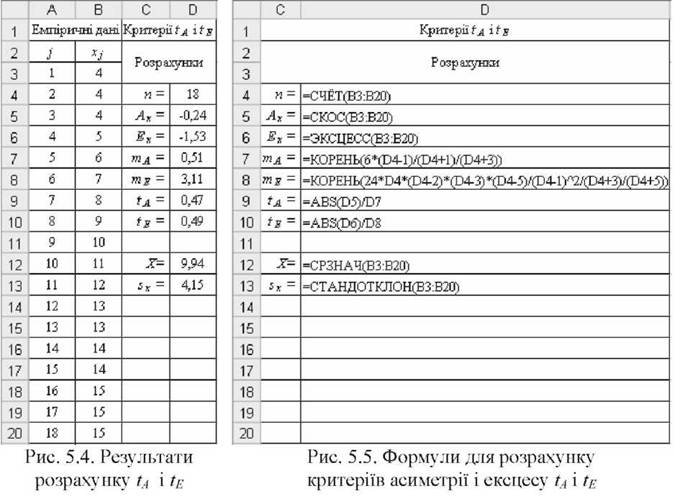
o Розрахунки емпіричних критеріїв t_A і t_E (рис. 5.4) виконано за допомогою формул (див. рис. 5.5). Вибіркові значення асиметрії (4_Х) та ексцесу (Е_х) за формулами (2.12а) і (2.126) розраховано за допомогою функцій MS Excel =СКОС() і =ЗКСЦЕСС().

o Формулювання висновків. Чисельні значення критеріїв t_A і t_E (рис. 5.4) не перевищують 3 (t_A ~ 0,47 < 3; t_E ~ 0,49 < 3), що дає можливість стверджувати про відсутність відмінностей між емпіричним і теоретичним нормальним розподілами.

Проте порівняння графіків цих розподілів дають підстави для сумніву щодо відповідності емпіричного розподілу нормальному законові (див. рис. 5.6), що потребує додаткової перевірки.

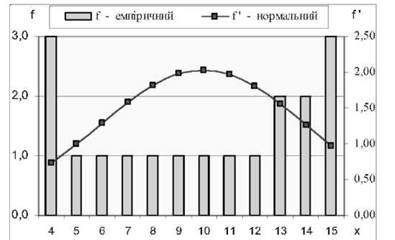
Рис. 5.6. Емпіричний і нормальний теоретичний розподіли

Більш того, у науковій і спеціальній літературі з математичної статистики при посиланні на критерії асиметрії й ексцесу як на засіб перевірки нормальності розподілу, нерідко звертається увага на застереження про те, що ці критерії дозволяють перевіряти лише деякі співвідношення між моментами розподілу і аж ніяк не є спроможними критеріями нормальності.