Математична статистика - Руденко В.М. - Критерій Вілкоксона-Манна-Вітні U

Статистика критерію Вілкоксона-Манна-Вітні²⁵ и визначається у такий спосіб. Всі Х-елементи першої і 7-елементи другої вибірки об'єднуються. Об'єднана вибірка х₁, х₂, х_п1, у₁, у₂, у_п2 (п₁ і п₂ - обсяги вибірок) упорядковуються за зростанням. Елементи першої вибірки х₁, х₂, х_п1 займають у загальному варіаційному ряді місця з номерами Я₁, Л₂, Л_п1, інакше кажучи, мають ранги Л₁, Л₂, Л_п1. Тоді сума рангів елементів першої вибірки є статистикою Вілкоксона Т_х:

Т_х = Л1+ ^2 + ...+ Лп1. (5.13)

Статистика Манна-Вітні и визначається формулою

п ■ (п + 1)

и = (п1 o + ^{х К}₂^х ' - Тх. (5.14)

Оскільки Т_х і и лінійно зв'язані, то часто мова йдеться не про два критерії - Вілкоксона і Манна-Вітні, а про один - критерій Вілкоксона-Манна-Вітні²⁶. Метод Манна-Вітні визначає зону значень між двома чисельними рядами, що перехрещуються. Чим менше емпіричне значення критерію и_ем", тим більш ймовірно, що відмінності достовірні. Коли обсяги обох вибірок безмежно зростають, розподіли статистик Вілкоксона і Манна-Вітні є асимптотично нормальними.

Приклад 5.8. За допомогою и-критерію перевірити припущення щодо однорідності вибірок (відмінності між показниками груп) за емпіричними даними прикладу 5.5).

Послідовність рішення:

o Формулювання гіпотез:

Н₀: відмінності у показниках ознаки не є статистично значущі;

Hf: відмінності у показниках ознаки є статистично значущі.

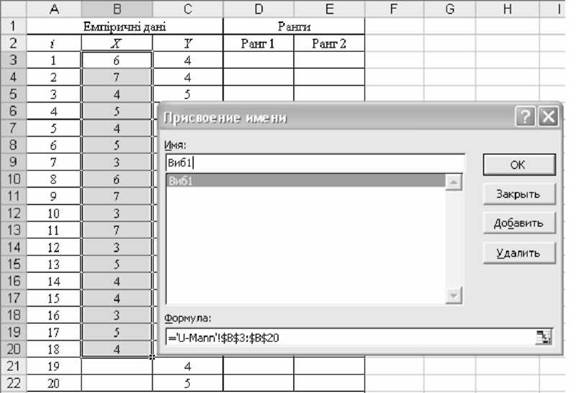
Рис. 5.20. Присвоєння імені "Виб1" діапазону даних $В$3:$В$20

o Розрахунки емпіричного критерію (рис. 5.20 і 5.21):

- присвоїти ім'я "Виб1" і "Виб2" двом вибіркам. Для цього виконати команди головного меню MS Excel [Вставка -> Ім'я -> Присвоїти...]. У діалоговому вікні (рис. 5.20) внести ім'я "Виб1" (ім'я записати без пробілів), а також діапазон комірок даних ($В$3:$В$20 - адреса абсолютна). Присвоїти ім'я "Виб2" діапазонові даних С3:С22 за аналогічними діями;

- виконати ранжирування значень вибірок, розглядаючи їх як одну об'єднану групу, приписуючи меншому значенню нижчий ранг (загальна кількість рангів п₁ + n₂). Для цього внести у стовпчики "Ранг 1" і "Ранг 2" відповідний вираз, який, наприклад, для комірки D3 виглядатиме як:

=(СЧЕТ(Виб1:Виб2) + 1 - РАНГ(В3;Виб1:Виб2; 1) -РАНГ(В3;Виб1:Виб2; 0))/2+РАНГ(В3;Виб1:Виб2;1);

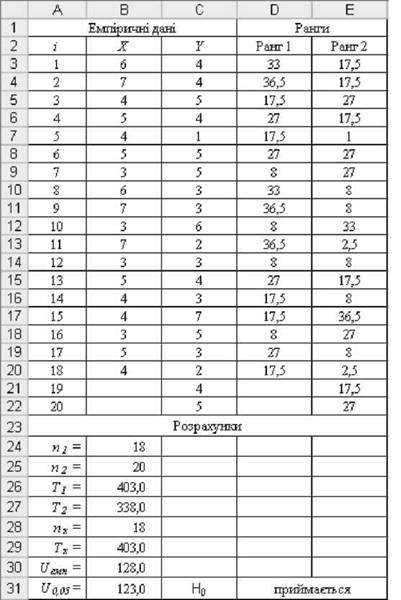
Рис. 5.21. Результати розрахунків критерію и_емп

- скопіювати вираз в інші комірки стовпчиків Б і Е;

- розрахувати обсяг вибірок п₁ і п₂. Для цього у комірку В24 внести вираз =СЧЕТ(Виб1), а у комірку В25 - вираз =СЧЕТ(Виб2);

- розрахувати суми рангів Т₁ і Т₂ для двох вибірок. У комірку В26 внести вираз =СУММ(03:020), у комірку В27 - вираз =СУММ(Е3:Е22);

- визначити обсяг п_х вибірки з більшою сумою рангів. У комірку В28 внести вираз =ЕСЛРІ(В26>В27;В24;В25);

- визначити Т_х - найбільшу з двох (Т₁ і Т₂ ) рангових сум. У комірку В24 внести вираз =ЕСЛИ(В26>В27;В26;В27);

- визначити емпіричне значення V-критерію за формулою: и_емп = (п ■ п_г) + ^Пх '^{(пх +1)} - Тх, (5.15)

де п_} і п₂ - обсяги вибірок; п_х - обсяг вибірки з більшою сумою рангів; Т_х - найбільша із двох рангових сум. Для цього у комірку В25 внести вираз =(В24*В25)+В28*(В28+1)/2-В29. ^"=128.00 (див. рис. 5.21).

o Визначення критичного значення и-критерію. За табл. 4 Додатків для п_} =18 і п₂ =20, а також а = 0,05 критичне значенняи₀₀₅ = 123.

o Прийняття рішення. Оскільки и_ем">и_0і05 (128>123), нульова гіпотеза Н₀ приймається на рівні 0,05. Зауваження: для и-критерію Н₀ приймається за умови и_емп > и_кр .

o Формулювання висновків. На рівні значущості 0,05 можна стверджувати, що відмінності у показниках ознаки не є статистично значущі.

Критерій Вілкоксона-Манна-Вітні придатний для статистичного аналізу даних, виміряних за порядковою шкалою. Проте у варіанті загальної альтернативи критерій не завжди дозволяє виявити розходження функцій розподілу. Для цього варіанту перевірки однорідності вибірок доцільно застосовувати критерій Лемана-Розенблатта со².