Математична статистика - Руденко В.М. - 5.5. ВИЯВЛЕННЯ ВІДМІННОСТЕЙ І ЗСУВУ У РІВНІ ОЗНАКИ

Виявлення відмінностей між двома, трьома і більше чинниками застосовується при оцінці вірогідності впливу тієї чи іншої методики навчання, тренінгу, психоаналітичних засобів на особистість або групу осіб. Встановлення відмінностей може розглядатися і як мета, дослідницький результат, і як етап, що дозволяє сформулювати нові гіпотези. Для оцінки відмінностей застосовують, наприклад, критерій Крускала-Волліса H.

Достовірні зміни ("зсуви") у вимірюваних показниках в результаті дії якихось чинників можуть стати об'єктивним показником у ефективності пси-холого-педагогічних досліджень. Статистично достовірні зсуви дозволять стверджувати, що експериментальні дії були істотними. Для оцінки вірогідності зсуву застосовують, наприклад, критерії Фрідмана Хг , Пейджа L.

Критерій Крускала-Волліса H

Критерій Крускала-Волліса н призначений для оцінки відмінностей одночасно між трьома, чотирма і т.д. вибірками за рівнем досліджуваної ознаки. Критерій Н дозволяє встановити, що мають місце відмінності ознаки при переході від групи до групи, але не вказує на напрям цих змін.

Гіпотези:

Н₀: між вибірками 1, 2, 3 і т.д. існують лише випадкові відмінності за рівнем досліджуваної ознаки;

Н₁: між вибірками 1, 2, 3 і т.д. існують невипадкові відмінності за рівнем досліджуваної ознаки.

Обмеження критерію: на рівні значущості а=0,05 допускається, щоб в одній із 3-х вибірок п = 3, а в двох інших п = 2; для а=0,01 необхідно, щоб у кожній вибірці п > 3.

Приклад 5.18. Дані опитувань позитивного ставлення (у %) студентів щодо відмови від "шкідливих звичок" (паління тютюну, вживання алкоголю тощо) представлено у таблиці рис. 5.43. Чи відрізняються середні показники позитивного ставлення студентів за різними роками навчання до важливості і необхідності "здорового способу життя"? В опитуванні приймали участь 6 груп студентів 1-го курсу, 5 груп 2-го і по чотири групи 3-го і 4-го курсів.

Послідовність рішення:

o Формулювання гіпотез:

Н₀: середні показники позитивного ставлення студентів до "здорового способу життя" не відрізняються для різних курсів;

Н₁: середні показники позитивного ставлення студентів до "здорового способу життя" відрізняються для різних курсів.

o Перевірка обмежень: виміри зроблено за шкалою інтервалів; кількість вибірок - чотири (с =4); вибірки незв'язані.

o Розрахунки емпіричного критерію Крускала-Волліса Н (рис. 5.43):

- присвоїти ім'я вибіркам: "Виб1", "Виб2", "Виб3", "Виб4" (послідовність і склад операцій див. у прикладі 5.8);

- підрахувати для вибірок: Обсяги, Суми, Середні за допомогою функцій MS Excel =СЧЕТ(), =СУММ() і =СРЗНАЧ();

- визначити ранги індивідуальних значень для загальної вибірки, що об'єднує всі чотири окремі вибірки. Для цього у стовпчики "Ранг1-Ранг4" внести математичні вирази. Наприклад, для комірки F3 це буде:

=(СЧЕТ(Виб1:Виб2:Виб3:Виб4) + 1 - PAHT(B3;Bh61:Bh62:Bh63:Bh64; 1) -PAHT(B3;Bh61:Bh62:Bh63:Bh64; 0))/2 + PAHT(B3;Bh61:Bh62:Bh63:Bh64;1);

- скопіювати вираз в інші комірки стовпчиків F:I ("Ранг1-Ранг4");

- для стовпчиків "Ранг1-Ранг4" підрахувати обсяги "j, суми рангів 7} і середні значення рангів за допомогою функцій =СЧЕТ(), =СУММ() і =СРЗНАЧ();

- визначити обсяг об'єднаної вибірки N = 6 + 5 + 4 + 4 = 19. Для цього у комірку В12 внести вираз =CYMM(B9:E9;

- визначити суму відносних квадратів рангів:

T = 2z - = 36²/6 + 40²/5 + 51²/4 + 63²/4 = 2178,50 (у комірку В13 внести

вираз =F10^A2/F9+G10^A2/G9+H10^A2/H9+I10^A2/I9);

- для розрахунку емпіричного значення Н-критерію за формулою:

внести у комірку В14 вираз =12/В12/(В12+1)*В13-3*(В12+1) і отримати значення критерію Н_ами=12/(19-(19+1)-2178,50-3-(19+1)=8,79 (див. рис. 5.43).

o Визначення критичного значення Н-критерію для кількості груп с < 5 зосереджено у відповідних таблицях, для с > 5 необхідно користуватися критичними значеннями /²-критерію. Для а=0,05 і 0,01 і ступенів вільності V = с-1 = 4-1= 3 значення х²₀,₀₅ і Хот можна отримати за допомогою функції =ХИ20БР(), яку внести у комірки В15 і В16 з відповідними аргументами: =ХИ20БР(0,05;3) і =ХИ20БР(0,01;3).

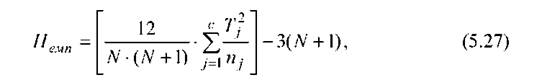
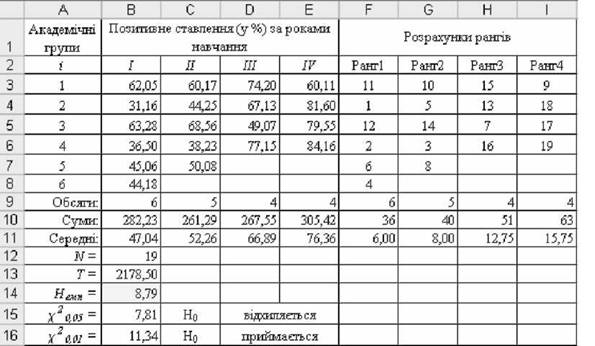
Рис. 5.43. Результати розрахунків критерію Н_емп

o Прийняття рішення. Оскільки Н_ем" > х²о,о₅ (8,79>7,81), але Н_емп< х²о,о₁ (8,79<11,34), нульова гіпотеза Н₀ відхиляється лише на рівні значущості 0,05 і приймається на рівні значущості 0,01.

o Формулювання висновків. На рівні значущості 0,05 середні показники позитивного ставлення студентів різних курсів до "здорового способу життя" відрізняються один від одного. Якщо ця різниця не може вважатися (на рівні значущості 0,05) достатньо переконливою, необхідно провести додаткові і більш ретельні дослідження.