Математична статистика - Руденко В.М. - Точково-бісеріальний коефіцієнт кореляції rpb

Для визначення тісноти зв'язку ознак X і Y, які оцінюються у двох значеннях 1 і 0, застосовується коефіцієнт <р Пірсона:

Я>= і , (5.32)

^Jpx ■ ^py ■ ⁽ⁿ - ^px ⁾ o ⁽ⁿ - ^py ⁾

де: p_xy - число об'єктів, що мають "1" і з X, і з Y; p_x і p_y - число об'єктів, що мають "1" з Xі з Yвідповідно; n - загальна кількість об'єктів.

Приклад 5.23. Оцінити зв'язаність між захопленістю учнів спортом та їхньою схильністю до математики. У таблиці рис. 5.50 позначення для X і Y: 1 -наявність ознаки, 0 - її відсутність.

Послідовність рішення:

o Розрахунки коефіцієнта <р проводимо за допомогою таких виразів:

- у комірку В15 внести вираз =СЧЕТ(В3:В14);

- у комірку В16 - вираз =СУММЕСЛИ(В3:В14;"=1";С3:С14);

- у комірку В17 - вираз =СУММ(В3:В14);

- у комірку В18 - вираз =СУММ(С3:С14);

- у комірку В19 - вираз =(В15*В16-В17*В18)/КОРЕНЬ(В17*В18*(В15-В17)*(В15-В18)). Звичайні арифметичні розрахунки дають аналогічний результат коефіцієнта кореляції <р Пірсона дляр_ху = 5,р_х = 6, р_у = 7 і п = 12:

12o5 - 6 o 7 у> = ~ 0,51.

д/6 o 7 o (12 - 6) o (12 - 7)

o Оцінка значущості коефіцієнта кореляції ^. Якщо прийняти, що вибірковий розподіл коефіцієнта ер приблизно описується нормальним законом з нульовим середнім і одиничним стандартним відхиленням, перевірка нуль-гіпотези виконується за допомогою г-критерію: г_емп = д) -4п .

Внести у комірку В20 вираз =В19*КОРЕНЬ(В15) і отримати 2_емп:

і_еяп = 0,51 -712 * 1,76.

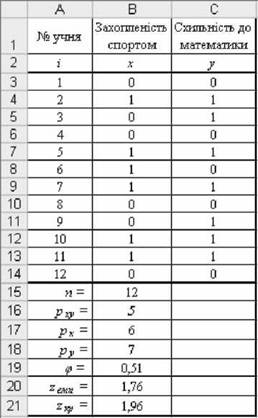
Рис. 5.50. Розрахунки коефіцієнта кореляції <р

o Критичне значення г-критерію для а=0,05 розташоване нижче г_о/2 стандартного нормального розподілу (0,025 або 0,975). У комірку В21 внести функцію =НОРМСТОБР(1-0,05/2), яка поверне значення г_кр ~ 1,96.

Висновки: оскільки г_ем"<і_кр (1,76<1,96), на рівні значущості 0,05 нульова гіпотеза Н₀ приймається. Отже, значення коефіцієнта ер ~ 0,51 не може свідчити про існування зв'язку між захопленістю спортом учнів і проявом схильності до математики.

Точково-бісеріальний коефіцієнт кореляції rpb

Точково-бісеріальний коефіцієнт кореляції г_рЬ використовується для емпіричних даних, значення яких отримано за різними шкалами вимірювань, наприклад, якщо змінна x вимірюється за дихотомічною шкалою, а змінна У - у шкалі інтервалів або відносин:

_ У1 - У 0 І п₁ ■ п₀ ^грь - лі : тг^{, (5.33)}

*у п ■ (п -1)

де У1 і п₁- середнє і кількість У об'єктів, що мають 1 з X; У0 і п₀ - середнє і кількість У об'єктів, що мають 0 з X; я_у - стандартне відхилення всіх п значень У; п = п₁ + п_{0 .} Приклад 5.24. Оцінити зв'язок між показниками "стать" і "зріст" рис. 5.51 для 15 підлітків (x = 1 для чоловічої, x = 0 для жіночої статі). Послідовність рішення:

o Розрахунки коефіцієнта кореляції г_рЬ :

- у комірку Е3 внести =СЧЕТ(Л3:Л12) і отримати п = 10;

- у комірку Е4 внести =СУММ(В3:В12) і отримати п₁=6;

- у комірку Е5 внести =Е3-Е4 і отримати п₀=4;

- у комірку Е6 внести =СУММЕСЛИ(В3:В12;1;С3:С12)/Е4 і отримати середній зріст хлопчиків У1 "167,83 см;

- у комірку Е7 внести =СУММЕСЛРІ(В3:В12;0;С3:С12)/Е5 і отримати середній зріст дівчат У0 ~ 154 см;

- у комірку Е8 внести =СТАНДОТКЛОН(С3:Є12) і отримати стандартне відхилення 5_у= 11,35;

- у комірку Е9 внести вираз для розрахунку точково-бісеріального коефіцієнта =(Е6-Е7)ІЕ8*КОРЕНЬ(Е4*Е5ІЕ3І(Е3-1)) і отримати його значення:

₌ ^167,83-¹⁵⁴ р^ _т 0,63

^рЬ 11,35 10 o (10-1) ■

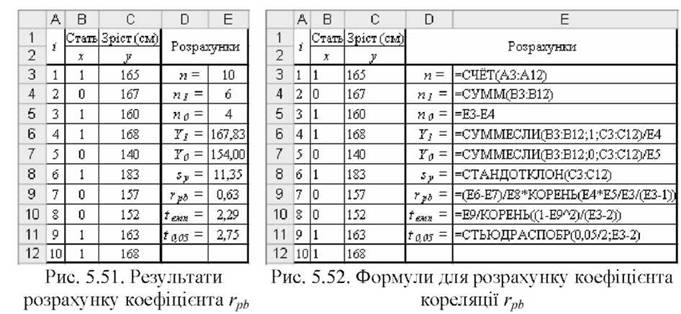
На рис. 5.51 представлено результати розрахунку точково-бісеріального коефіцієнта кореляції г"_ь, на рис. 5.52 - відповідні розрахункові формули.

o Оцінка значущості коефіцієнта кореляції г_рЬ зводиться до перевірки нуль-гіпотези (Н₀: г_рЬ = 0) , для якої використовується статистика ґ-критерій Стьюдента з (п-2) ступенями вільності:

ґ = , І* . (5.34)

^/(1 - гД )І(п - 2) ' '

Для розрахунку ґ_еля у комірку Е10 внести =Е9ІКОРЕНЬ((1-Е9^л2)І(Е3-2)) і отримати значення ґ_еля ~ 2,29.

o Критичне значення ґ-критерію можна отримати за допомогою функції =СТЬЮДРАСПОБР(<хІ2; п-2). При а =0,05 і п=10 у комірку В256 внести функцію =СТЬЮДРАСПОБР(0,05І2;Е3-2), яка дає значення ґ", = 2,75.

o Висновки: оскільки отримане значення ї_емп -2,29 не перевищує критичне значення ^-2,75 нуль-гіпотеза про відсутність кореляції приймається. Отже, з імовірністю 95% (а=0,05) правдоподібно, що у цій ситуації коефіцієнт кореляції г_рЬ , який приймає доволі суттєве значення (0,63), не є вірогідним!

Запитання. Завдання.

1. Охарактеризуйте особливості застосування, розрахунку і перевірки значущості коефіцієнта лінійної кореляції Пірсона.

2. Охарактеризуйте особливості застосування, розрахунку і перевірки значущості коефіцієнта рангової кореляції Спірмена.

3. Охарактеризуйте особливості застосування, розрахунку і перевірки значущості дихотомічного коефіцієнта кореляції Пірсона ^.

4. Охарактеризуйте особливості застосування, розрахунку і перевірки значущості точково-бісеріального коефіцієнта кореляції.

6. Повторіть математичні процедури завдань за прикладами 5.21 - 5.24.

7. Виконайте лабораторні роботи № 20 - № 22.