Математична статистика - Руденко В.М. - Критерій тенденцій Пейджа L

Критерій тенденцій Пейджа L застосовується для зіставлення показників, вимірюваних у трьох і більш умовах на одній і тій же вибірці випробовуваних. L-критерій дозволяє виявити тенденції у вимірі ознаки при переході від умови до умови. Його можна розглядати як розвиток критерію Фрідмана, оскільки він не тільки констатує розходження, але і вказує на напрямок змін.

Гіпотези:

Н₀: збільшення індивідуальних показників при переході від першої умови до другої, а потім до третьої і далі випадкове;

Н₁: збільшення індивідуальних показників при переході від першої умови до другої, а потім до третьої і далі невипадкове.

При формулюванні гіпотез мається на увазі нова нумерація умов, що відповідає передбачуваним тенденціям.

Обмеження критерію: кількість випробовуваних осіб повинна бути у межах 2 < п < 12, кожна особа має пройти с випробувань - 3 < с < 6.

Приклад 5.20. Чи підвищується самооцінка емпатичних здібностей студентів при їх послідовному переході з курсу на курс навчання в інституті (за даними прикладу 5.19)?

Послідовність рішення:

o Формулювання гіпотез:

Н₀: збільшення індивідуальних показників самооцінки емпатичних здібностей студентів при переході від курсу до курсу навчання випадкове;

Н₁: збільшення індивідуальних показників самооцінки емпатичних здібностей студентів при переході від курсу до курсу навчання невипадкове.

o Перевірка обмежень: виміри зроблені за шкалою інтервалів; кількість умов с = 4 (3 <с< 6); кількість випробовуваних п =10 (2<п<12); вибірки зв'язані.

o Розрахунки емпіричного критерію тенденцій Пейджа Ь_емп (рис. 5.45):

- визначити середнє самооцінки за кожною умовою (для кожного курсу навчання), для чого у комірку В13 внести вираз =СРЗНАЧ(Б3:Б12). Аналогічні вирази внести у комірки С13:Е13;

- проранжирувати індивідуальні значення самооцінки для кожного студента (ранжирування за рядками), нараховуючи меншому значенню менший ранг. Для цього у комірку В16 внести вираз

=(СЧЕТ($Б3:$Е3) + 1 - РАНГ(Б3;$Б3:$Е3; 1) -- РАНГ(Б3;$Б3:$Е3; 0))І2+РАНГ(Б3;$Б3:$Е3;1);

- аналогічні вирази внести у комірки всього діапазону В16:Е25;

- у комірках В26Е26 підрахувати суми рангів Т за кожною умовою;

- у комірках Р16:Р26 перевірити збіг отриманих сум за рядками і за стовпчиками;

- у комірки В27:Е27 внести значення нових індексіву: 1, 2, 3, с;

- у комірки В28:Е28 внести з клавіатури упорядковані за збільшенням значення сум рангів Т* за кожною умовою;

- у комірки В29 і В30 внести значення параметрів п і с за допомогою виразів =СЧЕТ(Л3:Л12) і =СЧЕТ(Б3:Е3);

- у комірку В31 внести вираз =СУММПРОИЗВ(Б27:Е27;Б28:Е28), який дозволить підрахувати емпіричне значення Ь_емп критерію Пейджа за формулою:

^" = Е(7 o Т*), (5.29)

7=1

де с - кількість умов; Т* - суми рангів за кожною умовою;] - індекси нової нумерації умов. Отримаємо емпіричне значення критерію Пейджа Ь_емп =

285,5.

o Визначити критичні значення критерію Пейджа Ь_кр для а=0,05 і 0,01 можна за табл.9 Додатків. Для параметрів с=4 і п=10 критичні значення такі:

^0,05 = ^266, 1^0,01 = ^272.

o Прийняття рішення. Оскільки Ь_емп > Ь₀₀₁ (285,5>272), нульова гіпотеза Н₀ відхиляється на рівні значущості 0,01 (див. рис. 5.45).

o Формулювання висновків. Між показниками самооцінки емпатичних здібностей, виміряними в різні роки навчання студентів у вищих навчальних закладах, існують невипадкові розходження. Збільшення індивідуальних показників при переході від умови до умови також є невипадковим.

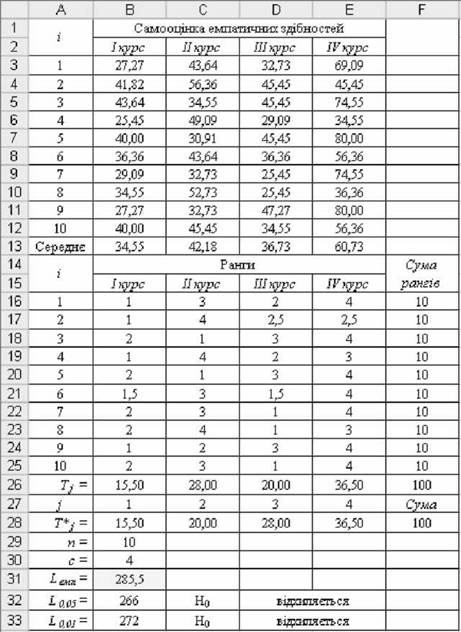
Рис. 5.45. Результати розрахунків ь_емп

Запитання. Завдання.

1. Для яких ситуацій використовується критерій Крускала-Волліса Н?

2. Для яких ситуацій використовується критерій Фрідмана /²_Г?

3. Для яких ситуацій використовується критерій тенденцій Пейджа ь?

4. Повторіть математичні процедури завдань за прикладами 5.18 - 5.20.

5. Виконайте лабораторні роботи № 18 і № 19.