Теорія статистики - Мармоза А.Т. - Середня гармонічна

Середня гармонічна є оберненою до середньої арифметичної, обчислену з обернених значень усереднюваної ознаки. Залежно від характеру наявного матеріалу її застосовують тоді, коли ваги доводиться не множити, а ділити на варіанти, або, що те саме, множити на обернене їх значення. Таким чином, середня гармонічна розраховується, коли відомі дані про обсяг ознаки (Ш=хф) і індивідуальні значення ознаки (х) і невідомі ваги (ф). Так як обсяги ознак являють собою добуток значень ознаки (х) на частоту ф, то частоту ф визначають якф = Ш: х.

Формули середньої гармонічної простої і зваженої мають вигляд:

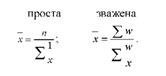
Як видно, середня гармонічна є перетвореною формою середньої арифметичної. Замість гармонічної завжди можна розрахувати середню арифметичну, попередньо визначивши ваги окремих значень ознаки. При обчисленні середньої гармонічної вагами є обсяги ознак.

Середня гармонічна проста застосовується у випадках, коли обсяги явищ по кожній ознаці рівні.

Наприклад, три комбайнера працюють на збиранні зернових культур. Перший комбайнер на збирання 1 га протягом 7-годинної зміни затрачав 35 хв, другий - 31 хв, третій - 33 хв. Потрібно визначити середні затрати праці на збирання 1 га зернових культур.

Розрахунок середніх затрат часу на збирання 1 га зернових культур за формулою середньої арифметичної простої був би правильним

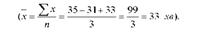
тоді, коли б усі комбайнери протягом зміни зібрали по 1 га або однакову кількість гектарів зернових культур. Проте протягом зміни окремими комбайнерами була зібрана різна площа зернових культур.

Неправомірність застосування формули середньої арифметичної пояснюється ще й тим, що показник затрат праці на одиницю робіт (збирання 1 га зернових культур) є оберненим до показника продуктивності праці (збирання зернових культур за одиницю часу).

Середній час, потрібний для збирання 1 га зернових культур по всіх комбайнерах визначимо як відношення затрат часу усіма комбайнерами до загальної кількості зібраних гектарів. У нашому прикладі немає відомостей про кількість фактично зібраних гектарів кожним комбайнером. Однак ці величини можна обчислити за таким співвідношенням:

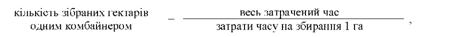
де весь затрачений час для кожного комбайнера становитиме 420 хв (7год o 60 хв).

Тоді середні затрати часу на збирання 1 га зернових культур можна визначити за формулою:

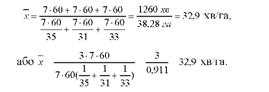
Розрахунки можна значно спростити, якщо використати формулу середньої гармонічної простої:

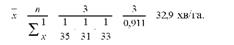
Отже, по цій сукупності комбайнерів на збирання 1 га зернових культур у середньому затрачається 32,9 хв.

Порядок розрахунку середньої гармонічної зваженої розглянемо на такому прикладі (табл. 4.3).

Таблиця 4.3. Дані для розрахунку середньої гармонічної зваженої

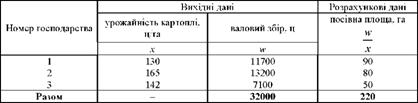
Оскільки середня урожайність являє собою відношення валового збору до площі посіву, то спочатку визначимо площу посіву картоплі по кожному господарству, а потім середню урожайність:

Відповідно до однієї з властивостей середня гармонічна не зміниться, якщо обсяги явищ, які є вагами окремих варіант, помножити або розділити на яке-небудь довільне число. Це дає змогу при її обчисленні користуватися не абсолютними показниками, а їх питомими вагами. Припустимо, потрібно визначити середню ціну реалізації картоплі за такими даними (табл.4.4).

Таблиця 4.4. Дані для розрахунку середньої ціни реалізації картоплі

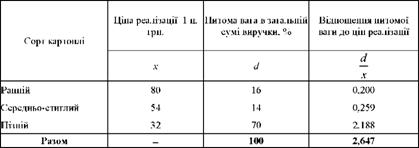
У наведеному прикладі відсутні дані про виручку від реалізації окремих сортів картоплі, яка являє собою добуток ціни реалізації 1 ц на кількість реалізованої картоплі. Тому замість обсягів явищ можна використати їх співвідношення, тобто питому вагу окремих сортів картоплі в загальній виручці. Використовуючи дані таблиці, визначимо середню ціну реалізації картоплі:

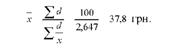
Середню гармонічну застосовують також для визначення середньої урожайності по групі однорідних культур, якщо відомі валовий збір і урожайність окремих культур, для обчислення середнього процента виконання плану виробництва і реалізації продукції по однорідній сукупності, якщо відомі дані про фактично вироблену або реалізовану продукцію і процент виконання плану по окремих об'єктах і т.д.