Теорія статистики - Мармоза А.Т. - Розділ 8. Дисперсійний аналіз

8.1. Теоретичні основи і принципова схема дисперсійного аналізу

Розглянуті вище прийоми перевірки статистичних гіпотез щодо істотності відмінностей між двома середніми на практиці мають обмежене застосування. Це пов'язано з тим, що для виявлення дії всіх можливих умов і факторів на результативну ознаку польові та лабораторні досліди, як правило, проводять із застосуванням не двох, а більшого числа вибірок (1220 та більше).

Часто дослідники порівнюють середні кількох вибірок, об'єднаних у єдиний комплекс. Наприклад, вивчаючи вплив різних видів і доз добрив на урожайність сільськогосподарських культур досліди повторюють у різних варіантах. У цих випадках попарні порівняння стають громіздкими, а статистичний аналіз усього комплексу потребує застосування особливого методу. Такий метод, розроблений в математичній статистиці, дістав назву дисперсійного аналізу. Вперше його застосував англійський статистик Р. Фішер при обробці результатів агрономічних дослідів (1938 р.).

Дисперсійний аналіз - це метод статистичної оцінки надійності проявлення залежності результативної ознаки від одного або кількох факторів. За допомогою методу дисперсійного аналізу проводиться перевірка статистичних гіпотез відносно середніх в кількох генеральних сукупностях, які мають нормальний розподіл.

Дисперсійний аналіз є одним з основних методів статистичної оцінки результатів експерименту. Все більш широке застосування отримує він і в аналізі економічної інформації. Дисперсійний аналіз дає змогу встановити, наскільки вибіркові показники зв'язку результативного і факторних ознак достатні для поширення одержаних за вибіркою даних на генеральну сукупність. Достоїнством цього методу є те, що він дає досить надійні висновки по вибірках невеликої чисельності.

Досліджуючи варіацію результативної ознаки під впливом одного або кількох факторів за допомогою дисперсійного аналізу можна одержати крім загальних оцінок істотності залежностей, також і оцінку відмінностей у величині середніх, що формуються при різних рівнях факторів, та істотності взаємодії факторів. Дисперсійний аналіз застосовується для вивчення залежностей як кількісних, так і якісних ознак, а також при їх поєднанні.

Суть цього методу полягає в статистичному вивченні вірогідності впливу одного або кількох факторів, а також їх взаємодії на результативну ознаку. Відповідно до цього за допомогою дисперсійного аналізу вирішуються три основних завдання: 1) загальна оцінка істотності відмінностей між груповими середніми; 2) оцінка вірогідності взаємодії факторів; 3) оцінка істотності відмінностей між парами середніх. Найчастіше такі завдання доводиться вирішувати дослідникам при проведенні польових і зоотехнічних дослідів, коли вивчається вплив кількох факторів на результативну ознаку одночасно.

Принципова схема дисперсійного аналізу включає встановлення основних джерел варіювання результативної ознаки і визначення обсягів варіації (сум квадратів відхилень) за джерелами її утворення; визначення числа ступенів свободи, що відповідають компонентам загальної варіації; обчислення дисперсій як відношення відповідних обсягів варіації до їх числа ступенів свободи; аналіз співвідношень між дисперсіями; оцінка вірогідності різниці між середніми і формулювання висновків.

Зазначена схема зберігається як при простих моделях дисперсійного аналізу, коли дані групуються за однією ознакою, так і при складних моделях, коли дані групуються за двома і більшим числом ознак. Однак із збільшенням числа групувальних ознак ускладнюється процес розкладання загальної варіації за джерелами її утворення.

Відповідно до принципової схеми дисперсійний аналіз можна подати у вигляді п'яти послідовно виконуваних етапів:

1) визначення і розкладання варіації;

2) визначення числа ступенів свободи варіації;

3) обчислення дисперсій та їх співвідношень;

4) аналіз дисперсій та їх співвідношень;

5) оцінка вірогідності різниці між середніми і формулювання висновків з перевірки нульової гіпотези.

Найбільш трудомісткою частиною дисперсійного аналізу є перший етап - визначення і розкладання варіації за джерелами її утворення. Порядок розкладання загального обсягу варіації докладно розглядався в розділі 5.

В основі розв'язування задач дисперсійного аналізу лежить закон розкладання (додавання) варіації, відповідно до якого загальна варіація (коливання) результативної ознаки поділяється на дві: варіацію, зумовлену дією досліджуваного фактора (факторів), і варіацію, викликану дією випадкових причин, тобто

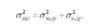
Припустимо, що досліджувана сукупність поділена за факторною ознакою на кілька груп, кожна з яких характеризується своєю середньою величиною результативної ознаки. При цьому варіацію цих величин можна пояснити двома видами причин: такими, які діють на результативну ознаку систематично і піддаються регулюванню в ході здійснюваного експерименту і такими, які регулюванню не піддаються. Очевидно, що міжгрупова (факторна або систематична) варіація залежить переважно від дії досліджуваного фактора, а внутрішньогрупова (залишкова або випадкова) - від дії випадкових факторів.

Щоб оцінити вірогідність відмінностей між груповими середніми, необхідно визначити міжгрупову та внутрішньогрупову варіації. Якщо міжгрупова (факторна) варіація значно перевищує внутрішньогрупову (залишкову) варіацію, то фактор впливав на результативну ознаку, істотно змінюючи значення групових середніх величин. Але виникає питання, яке співвідношення між міжгруповою і внутрішньогруповою варіаціями можна розглядати як достатнє для висновку про вірогідність (істотність) відмінностей між груповими середніми.

Для оцінки істотності відмінностей між середніми і формулювання висновків з перевірки нульової гіпотези (Н0 :х1 = х2 =... = хп) в дисперсійному аналізі використовується своєрідний норматив - Г-критерій, закон розподілу якого встановив Р.Фішер. Цей критерій являє собою відношення двох дисперсій: факторної, породжуваної дією досліджуваного фактора, та залишкової, зумовленої дією випадкових причин:

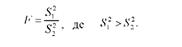
Дисперсійне відношення Г= £>і : £*2 американським статистиком Снедекором запропоновано позначати літерою Г на честь винахідника дисперсійного аналізу Р.Фішера.

Дисперсії °2 іо2 є оцінками дисперсії генеральної сукупності. Якщо вибірки з дисперсіями °2 і °2 зроблені з однієї і тієї самої генеральної сукупності, де варіація величин мала випадковий характер, то розбіжність у величинах °2 і °2 також випадкова.

Якщо в експерименті перевіряють вплив кількох факторів (А, В, С і т.д.) на результативну ознаку одночасно, то дисперсія, що обумовлена дією кожного з них, має бути порівняна з °е.гР , тобто

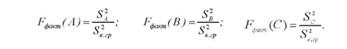
Якщо значення факторної дисперсії значно більше залишкової, то фактор істотно впливав на результативну ознаку і навпаки.

В багатофакторних експериментах крім варіації, зумовленої дією кожного фактора, практично завжди є варіація, яка зумовлена взаємодією факторів ($ав: ^лс ^вс $лііс). Суть взаємодії полягає в тому, що ефект одного фактора істотно змінюється на різних рівнях другого (наприклад, ефективність якості Грунту при різних дозах добрив).

Взаємодія факторів також має бути оцінена шляхом порівняння відповідних дисперсій 3 ^в.гр :

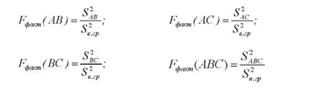
При обчисленні фактичного значення Б-критерію в чисельнику береться більша з дисперсій, тому Б > 1. Очевидно, що чим більше критерій Б, тим значнішими є розбіжності між дисперсіями. Якщо Б = 1, то питання про оцінку істотності відмінностей дисперсій знімається.

Для визначення меж випадкових коливань відношення дисперсій Р. Фішер розробив спеціальні таблиці Б-розподілу (дод. 4 і 5). Критерій Б функціонально зв'язаний з імовірністю і залежить від числа ступенів свободи варіації к1 і к2 двох порівнюваних дисперсій. Звичайно використовуються дві таблиці, що дозволяють робити висновки про гранично високе значення критерію Б для рівнів значущості 0,05 і 0,01. Рівень значущості 0,05 (або 5%) означає, що тільки в 5 випадках із 100 критерій Б може приймати значення, що дорівнює вказаному в таблиці або вище його. Зниження рівня значущості з 0,05 до 0,01 призводить до збільшення значення критерію Б між двома дисперсіями в силу дії тільки випадкових причин.

Значення критерію Б також залежить безпосередньо від числа ступенів свободи двох порівнюваних дисперсій. Якщо число ступенів свободи прямує до нескінченості (к-мо), то відношення Б для двох дисперсій прямує до одиниці.

Табличне значення критерію Б показує можливу випадкову величину відношення двох дисперсій при заданому рівні значущості і відповідному числі ступенів свободи для кожної з порівнюваних дисперсій. В зазначених таблицях наводиться величина Б для вибірок, зроблених з однієї і тієї самої генеральної сукупності, де причини зміни величин тільки випадкові.

Значення Г знаходять за таблицями (дод. 4 і 5) на перетині відповідного стовпця (число ступенів свободи для більшої дисперсії - к1) і рядка (число ступенів свободи для меншої дисперсії - к2). Так, якщо більшій дисперсії (чисельник Г) к1 = 4, а меншій (знаменник Г) к2 = 9, то Га при рівні значущості а = 0,05 становитиме 3,63 (дод. 4). Отже, в результаті дії випадкових причин, оскільки вибірки малочисельні, дисперсія однієї вибірки може при 5%-ному рівні значущості перевищувати дисперсію другої вибірки в 3,63 раза. При зниженні рівня значущості з 0,05 до 0,01 табличне значення критерію Г, як зазначалося вище, буде збільшуватися. Так, при тих самих ступенях свободи к1 = 4 і к2 = 9 і а = 0,01 табличне значення критерію Г становитиме 6,99 (дод. 5).

Розглянемо порядок визначення числа ступенів свободи в дисперсійному аналізі. Число ступенів свободи, що відповідає загальній сумі квадратів відхилень, розкладається на відповідні компоненти аналогічно розкладанню сум квадратів відхилень (^заг = №^гр + ]¥вгр) , тобто загальне число ступенів свободи (к") розкладається на число ступенів свободи для міжгрупової (к1) і внутрішньогрупової (к2) варіацій.

Так, якщо вибіркова сукупність, що складається з N спостережень, поділена на т груп (число варіантів досліду) і п підгруп (кількість повторностей), то число ступенів свободи к відповідно становитиме:

а) для загальної суми квадратів відхилень (й7заг)

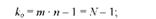
б) для міжгрупової суми квадратів відхилень ^м.гР)

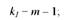
в) для внутрішньогрупової суми квадратів відхилень уУв.гР)

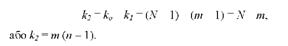
Згідно з правилом додавання варіації:

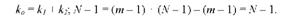
Наприклад, якщо в досліді сформовано чотири варіанти досліду (т = 4) у п'яти повторностях кожен (п = 5), і загальна кількість спостережень N = = т o п = 4 o 5 = 20, то число ступенів свободи відповідно дорівнює:

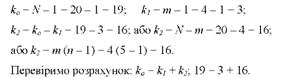
Знаючи суми квадратів відхилень і число ступенів свободи, можна визначити незміщені (скориговані) оцінки для трьох дисперсій:

Нульову гіпотезу Н0 за критерієм Б перевіряють так само, як і за і-критерієм Стьюдента. Щоб прийняти рішення з перевірки Н0, необхідно розрахувати фактичне значення критерію і порівняти його з табличним значенням Ба для прийнятого рівня значущості а і відповідного числа ступенів свободи к1 і к2 для двох дисперсій.

Якщо Бфакг > Ба, то згідно з прийнятим рівнем значущості можна зробити висновок, що відмінності вибіркових дисперсій визначаються не лише випадковими факторами; вони істотні. Нульову гіпотезу в цьому випадку відхиляють і є підстава стверджувати, що фактор істотно впливає на результативну ознаку. Якщо ж < Ба, то нульову гіпотезу приймають і є підстава стверджувати, що відмінності між порівнюваними дисперсіями знаходяться в межах можливих випадкових коливань: дія фактора на результативну ознаку не є істотною.

Застосування тієї або іншої моделі дисперсійного аналізу залежить як від кількості досліджуваних факторів, так і від способу формування вибірок.

Залежно від кількості факторів, що визначають варіацію результативної ознаки, вибірки можуть бути сформовані за одним, двома і більшим числом факторів. Відповідно до цього дисперсійний аналіз поділяється на однофакторний і багатофакторний. Інакше його ще називають однофакторним і багатофакторним дисперсійним комплексом.

Схема розкладання загальної варіації залежить від формування груп. Воно може бути випадковим (спостереження однієї групи не пов'язані із спостереженнями другої групи) і невипадковим (спостереження двох вибірок пов'язані між собою спільністю умов експерименту). Відповідно дістають незалежні і залежні вибірки. Незалежні вибірки можуть бути сформовані як з рівною так і з нерівною чисельністю. Формування залежних вибірок передбачає їх рівну чисельність.

Якщо групи сформовані у невипадковому порядку, то загальний обсяг варіації результативної ознаки включає в себе поряд з факторною (міжгруповою) і залишковою варіацією варіацію повторностей, тобто

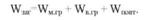
На практиці в більшості випадків доводиться розглядати залежні вибірки, коли умови для груп і підгруп вирівнюються. Так, у польовому досліді всю ділянку розбивають на блоки, з максимально вирівняннями умовами. При цьому кожен варіант досліду отримує рівні можливості бути представленим в усіх блоках, чим досягається вирівнювання умов для всіх перевірюваних варіантів, досліду. Такий метод побудови досліду дістав назву методу рендомізованих блоків. Аналогічно проводяться і досліди з тваринами.

При обробці методом дисперсійного аналізу соціально-економічних даних необхідно мати на увазі, що в силу багаточисельності факторів та їх взаємозв'язку важко навіть при самому ретельному вирівнюванні умов встановити ступінь об'єктивного впливу кожного окремого фактора на результативну ознаку. Тому рівень залишкової варіації зумовлюється не тільки випадковими причинами, але й суттєвими факторами, які не були враховані при побудові моделі дисперсійного аналізу. Внаслідок цього залишкова, дисперсія як база порівняння інколи стає неадекватною своєму призначенню, вона явно завищується за величиною і не може виступати як критерій істотності впливу факторів. В зв'язку з цим при побудові моделей дисперсійного аналізу стає актуальною проблема відбору найважливіших факторів і вирівнювання умов для проявлення дії кожного з них. Крім того. застосування дисперсійного аналізу передбачає нормальний або близький до нормального розподіл досліджуваних статистичних сукупностей. Якщо ця умова не витримується, то оцінки, одержані в дисперсійному аналізі, виявляться перебільшеними.