Математична статистика - Руденко В.М. - Розподіли випадкових величин

Розподіли випадкових величин

Випадкова величина - це величина, яка в результаті випробувань може приймати певні значення (із сукупності своїх значень) з певною ймовірністю. Випадковою можна назвати будь-яку (не обов'язково чисельну) змінну x, значення якої х створюють множину випадкових елементарних подій {х}.

Розрізняють дискретну і неперервну випадкові величини.

Дискретною випадковою величиною називається випадкова величина, що приймає скінчене число значень з множини, елементи якої можна пронумерувати. Неперервною випадковою величиною називається випадкова величина, можливі значення якої неперервно заповнюють деякий інтервал.

Рядок розподілу дискретної випадкової величини x може бути представлений як у табличній формі - у вигляді таблиці, де перераховано значення випадкової величини х₁, х₂, х_п з відповідними до них ймовірностямир₁, р₂, р_п (див. табл. 3.2), так і у вигляді графічного зображення (рис. 3.7).

Таблиця 3.2

Рядок розподілу дискретної випадкової величини X

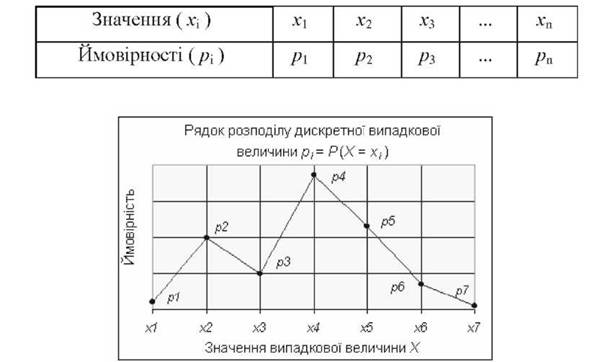
Рис. 3.7. Графік розподілу дискретної випадкової величини X

Рядок розподілу може мати аналітичну форма представлення, наприклад:

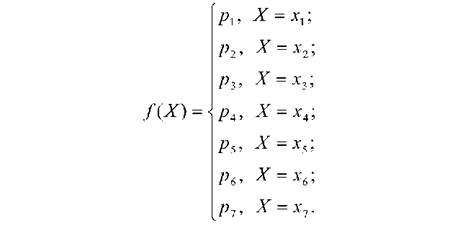
В загальному вигляді це можна записати якД(Х) = Р(Х=х) - значення функції /(X) дорівнює ймовірності Р(Х=х) того, що змінна X приймає значення х.

За аналогією з випадковими подіями, можна вважати, що простором елементарних випадкових значень х₁, х₂, х_п змінної X є скінчена множина цих значень С1={х}. Кожному елементарному значенню х₁, х₂, х_п, яке належить до множини СІ, поставлено у відповідність невід'ємне число - ймовірностір₁, р₂, р_п, тобто р! = Р(Х = х{) > 0, причому сума ймовірностей появи всіх елементарних значень змінної x дорівнює одиниці:

Р, = 1. (3.14)

Отже, пару {СІ, Р} можна вважати імовірнісним простором, який складається зі скінченої множини значень О змінної x і невід'ємної функції Р, яка визначена на множині значень О і задовольняє умові (3.14).

Якщо емпіричні дані є результат статистичних випробувань, то емпіричний розподіл частот можна також трактувати як розподіл випадкової величини - співвідношення можливих значень з відповідними ймовірностями їхньої появи. Оскільки класичні ймовірності збігаються з відносними частотами (див. поняття класичної ймовірності), то розподіли частот можна представляти як відповідні розподіли випадкових величин, проте, лише за певними умовами і обмеженнями (мова про них йтиме нижче).

Розглянемо на прикладі побудову розподілу дискретної випадкової величини.

Приклад 3.11. Розрахувати розподіл кількості виконаних завдань за результатами тестування навмання відібраної з академічного потоку вибірки студентів обсягом 20 осіб (табл. 3.3).

Таблиця 3.3

Кількість виконаних завдань

Послідовність рішення:

o представити емпіричні дані табл. 3.3 значеннями хі і відповідними абсолютними частотами виконання завдань. Частоти розрахувати за будь-яким відомим методом і внести у комірки Л3:С9. Сума абсолютних частот по-

7

винна скласти обсяг вибірки, тобто ^ т_і = 20 (див. комірку С10 рис. 3.8);

і=1

o для розрахунку ймовірностейр = Р(Х = хї) внести в комірку вираз

=С3/$С$10, аналогічні вирази внести у комірки 04:09;

o розрахувати в комірках Е3:Е9 ймовірності р,- = Р(Х < хі);

o побудувати графіки розподілу ймовірностей (рис. 3.9).

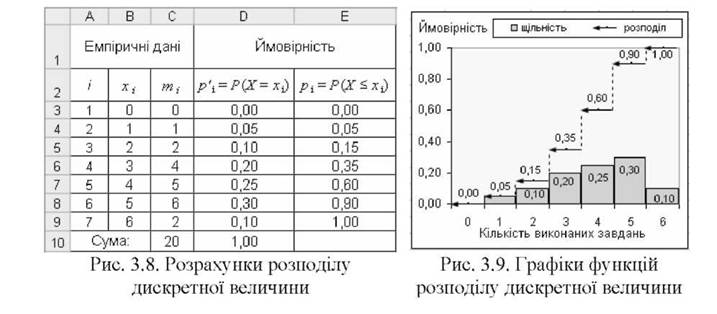
Отже, у таблиці рис. 3.8 розраховано розподіли ймовірностей дискретної змінної X (кількості виконаних завдань) р'(х) = Р(Х = х) і р(х) = Р(Х< х), на рис. 3.9 зображено відповідні графіки.

Сукупність ймовірностей р'і = Р(Х = хі) має назву щільності розподілу змінної X (див. стовпчик Б рис. 3.8 і гістограму рис. 3.9). Кожне окреме значення щільності розподілу визначає ймовірність р',- кожного окремого значення X! змінної X , тобто Р(Х = хі). Сума ймовірностей р',- усіх елементарних значень X! змінної X (за умови повної системи випадкових значень) дорівнює

п

одиниці, тобто ^ р] = 1. Як бачимо з рис. 3.8 (див. комірку 010), ця вимога

і=1

виконується: 0,00+0,05+0,10+0,20+0,25+0,30+0,10= 1,00.

Сукупність ймовірностей р! = Р(Х < X!) має назву розподілу змінної X (див. стовпчик Е рис. 3.6 і дискретний графік рис. 3.7 у вигляді сходинок з насиченням до 1,00). Розподіл випадкової величини показує ймовірність для змінної X, значення якої не перевищує х^ , тобто Р(Х < х^. Кожне значення розподілу є сумою ймовірностей р'і усіх попередніх елементарних значень х, і

змінної X, тобто: р_і =^р'_І. Наприклад, для і = 4 значення ймовірність р₄

і=1

4

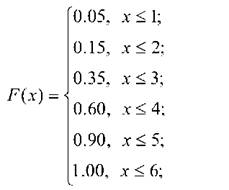
Аналогічно може бути представлено й щільність розподілу Дх). Для дискретної змінної розподіл і щільність розподілу зв'язані співвідношенням:

Р (хі) = ±/ (х,) (3.17)

і=1

Для неперервної змінної можна записати такі співвідношення:

- щільність розподілу Дх) = Р '(х). Це значить, що щільність Дх) є першою похідною від функції розподілу Р(х);

- щільність розподілу для будь-якої випадкової величини невід'ємна, тобто Лх) > 0, і має таку властивість:

складатиме р₄ р'. = 0,00 + 0,05 + 0,10 + 0,20 = 0,35 (див. комірку Е6 рис. 3.6).

¡=1

Ймовірність отримання у випробуванні будь-якого значення з повної системи випадкових значень (фактично, це є ймовірність достовірної події) дорівнює

п

одиниці. І дійсно, для і = п ймовірність р_п = ^ р] = 1(див. комірку Е9 рис. 3.6

і=1

або останнє значення ймовірності розподілу на графіку рис. 3.7).

Законом розподілу випадкової величини є співвідношення, що встановлює зв'язок між можливими значеннями випадкової величини і відповідними до них ймовірностями. Закон розподілу може бути задано функціями:

o функцією розподілу Р(х)

Р(х) = Р(Х < х); (3.15)

o функцією щільності розподілуДх)

Дх) = Р(Х = х). (3.16)

Для дискретної змінної функція розподілу Р(х) може бути представлена в аналітичній формі. Так, заданими рис. 3.8 функція Р(х) матиме вигляд:

Математичний аналіз надає геометричну інтерпретацію визначеному інтегралові (3.18) як площі (див. зафарбовану площу на рис. 3.10), яка зверху обмежена графіком функції /(х), а знизу - віссю абсцис у межах -ю < х < +со. Розмір площі за інтегралом (3.18) дорівнює одиниці.

Значення функції розподілу ¥(х) для певного значення х (наприклад, х = а) визначається через щільність розподілу /(х) за формулою:

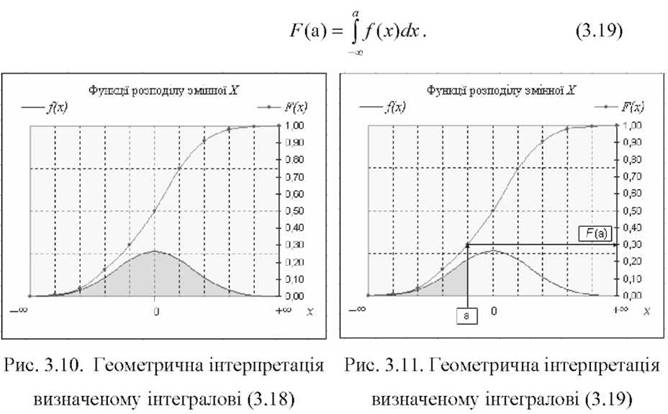
Інтеграл (3.19) і функція ¥(а) розподілу також мають сенс площі (див. зафарбовану площу на рис. 3.11), яка обмежена з трьох боків: зверху - графіком функції Дх), знизу - віссю абсцис у межах -" < х < а, з правого боку -ординатою, яка проходить через точку х = а.

Для х = +со функція розподілу ¥(со)=1, тобто

і (со) = / (х)^х = 1. (3.20)

-ОС

Отже, порівнюючи алгебру випадкових подій з математичним апаратом випадкової величини, можна дійти до висновку про те, що розподіли випадкових величин ізоморфно відтворюються на розподілах випадкових подій.

Розглянемо приклад розподілу неперервної випадкової величини.

Приклад 3.12. Як відомо з психодіагностики, коефіцієнт інтелекту О (показник інтелектуального розвитку сукупності однакових за віком осіб) розподіляється за законом, близьким до нормального¹², щільність розподілу якого визначається формулою:

гґ ¹ -0,5((х-1в)/<7)² _{г г}, . 1 | (х - І0² і

де /(х) - ймовірність Р(І<2 = х) того, що ї<2 прийме значення х; І<2 і а -середнє арифметичне і стандартне відхилення генеральної сукупності; % ~ 3,14; е ~ 2,71. Для певного контингенту індивідуумів середнє значення 1<2=100 і а =15.

Завдання: Побудувати розподіл коефіцієнта інтелекту І£) в діапазоні значень від І<2_МІН = 50 до І(2макс = 150. Визначити ймовірності того, що І(2 прийматиме значення: а) І£) < 80; б) Щ > 110; в) у межах 70 < І£) < 90; г) прийматиме значення поза межами інтервалу 80 < Щ < 120.

Рішення:

Розрахуємо значення щільності/(х) нормального розподілу і розподіл і(х) у табличній формі в указаному діапазоні з інтервалом 10 (рис. 3.10). Деталі розрахунку розглянемо пізніше у відповідному розділі. Важливим моментом є досягнення так званої нормалізації, за умови якої площа під кривою щільності розподілу /(х) повинна дорівнювати одиниці. Як бачимо з комірки С14 рис. 3.10, ця вимога виконується.

Побудуємо відповідні графіки розподілу І£) (рис. 3.13). Форма графіка щільності /(ІО) має вигляд "дзвону". Вона є симетричною відносно середнього значення ІО=100. Графік розподіл досягає насичення на рівні 1,00.

¹² Докладніше щодо нормального закону розподілу див. розділ 3.4.

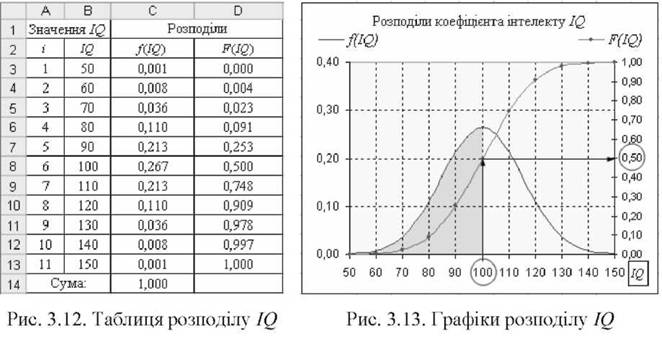
Слід звернути увагу на те, що ймовірність Р(/£> < 100) = 0,50. Інакше кажучи, ймовірність отримати значення 12 на рівні не більше середнього значення ї<2=100 складає 50%. На рис. 3.13 це відповідає зафарбованій площі, яка складає 50% від загальної. Аналітично це можна записати так:

100

Р (х < 100) = | / (х)Сх = 0,50.

-сс

Розглянемо пункти завдання щодо визначення ймовірності отримання конкретних значень коефіцієнта інтелекту

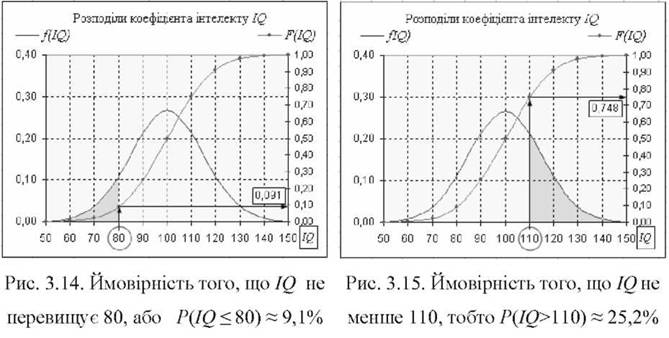
а) Визначити ймовірність того, що 12 прийматиме значення не більше 80, тобто Р(ї<2 < 80). Цій ситуації відповідає зафарбована площа рис. 3.14, для якої Р(80) ~ 0,091 (значення 0,091 можна отримати з табл. рис. 3.12). Аналітичний запис має вигляд:

80

Р(х < 80) = | Л(х)сІх ~ 0,091.

-сс

Отже, ймовірність Р(І<2 < 80) = 0,091 = 9,1%.

б) Визначити ймовірність того, що значення 12 не менше 110, тобто ,Р(/0>110). Зафарбована площа рис. 3.15 відповідає ситуації, коли треба отримати подію ^4{/2>110}, яка є доповненням протилежної події А{ї<2 < 110}. Сума ймовірностей протилежних подій дорівнює одиниці. Звідси ймовірність бажаної події Р(І2>110) = 1 - Р(ї(2 < 110) і аналітичний запис для визначення відповідної ймовірності за допомогою функцій розподілу такий:

110

Р(х > 110) = 1 - Р(х < 110) = 1 - | Л(х)Сх = 1 - 0,748 = 0,252.

-сс

Значення Р(110) = 0,748 можна отримати з табл. рис. 3.12. Отже, ймовірність Р(/((>110) ~ 25,2%.

в) Визначити ймовірність того, що ¡2 прийматиме значення не менше 70, але не більше 90, тобто Р(70< ¡2 <90). Зафарбована площа рис. 3.16 відповідає ситуації, коли з події ^{¡2 < 90} треба вилучити елементи події А₂{12 < 70}. Тоді ймовірність Р(А) бажаної події А дорівнюватиме різниці ймовірностей Р(40 і Р(А,) подій А_х і ^2, тобто Р(70< 1(2 < 90) = Р(/( < 90) - Р(Р2 < 70). Визначення ймовірності за допомогою функцій розподілу матиме вигляд:

90 90 70

| Л(х)Сх = | Л(х)Сх - | Л(х)Сх = Р(90) - Р(70), або

Р(90) - Р(70) = 0,253 - 0,023 = 0,23. Отже, ймовірність Р(70< ¡2 < 90) = 23%.

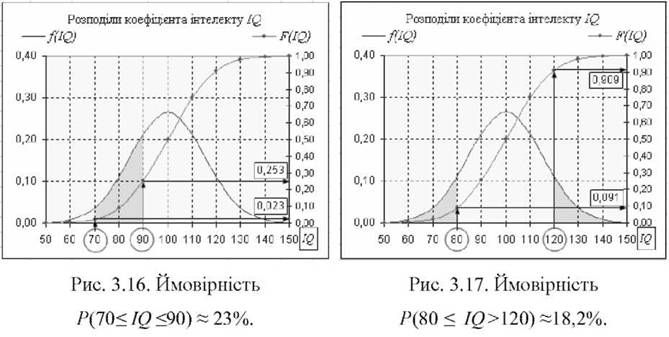
г) Визначити ймовірність того, що І<О прийматиме значення поза межами інтервалу 80 < О < 120, тобто ,Р(80 > О >120). Цій події відповідає сума двох зафарбованих частин площі рис. 3.17. Рішення можна отримати у 2-х варіантах:

1-й варіант. Подія А складається з двох несумісних подій А₁{І<2 < 80} і ^₂{І<2 >120} з ймовірностями Р(АА і Р(А₂) відповідно. Ймовірність Р(АА події А₁ визначиться як

80

|/(х)ах = і(80), або з табл. рис. 3.12 маємо і(80) = 0,091.

Ймовірність Р(А₂) події ^4₂ визначиться як доповнення до протилежної події І2{ІО< 120} або Р(А₂) = 1 - ~Аі{ІО< 120}, а саме

120

і(х > 120) = 1 - | /(х)йх = 1 - і(120) або

-ос

120

і(х > 120) = 1 - і(х < 120) = 1 - | /(х)ох = 1 - 0,909 ~ 0,091.

-ос

Ймовірність Р(А) події А складається з суми ймовірностей Р(АА і Р(А₂) подій А₁ і А₂, тобто Р(А) = Р(А₁) + Р(А₂) = 0,091 + 0,091 ~ 0,182 = 18,2%.

2-й варіант. Подію ^4{80>І< >120} можна звести і розглядати як доповнення до протилежної події А, яку позначимо _8{80 <І(2 < 120} (див. незафарбовану площу рис. 3.17). Тоді Р(А) = 1- Р(В).

Подія _8{80< ¡2 <120} відповідає попередній ситуації (див. вище п. "в"), коли з події В₁ {¡2 < 120} треба вилучати елементи події В₂{2< 80}. Ймовірність Р(В) події В є різниця ймовірностей Р(В{) і Р(В₂)

Р(В) = Р(12 < 120) - Р(12 < 80). Ймовірність Р(А) бажаної події А дорівнюватиме

Р(А) = 1- Р(В) = 1 - [Р(Щ < 120) - Р(12 < 80)]. Визначення ймовірності за допомогою функцій розподілу матиме вигляд:

120 Г120 80 ~|

1 - | Л(х)Сх = 1 - | Л(х)Сх - | Л(х)Сх = 1 - [Р(120) - Р(80)], або 1- [Р(120) - Р(80)] = 1 - [0,909 - 0,091] = 1- 0,818 = 0,182 = 18,2%.

Отже, ймовірність того, що ¡2 не прийматиме значення в діапазоні від 80 до 120, тобто Р(80 > ¡2>120), складає 18,2%.

Зауваження: якщо графік розподілу симетричний і зафарбовані площі однакові за розміром, ймовірність Р(А) розраховується як подвоєна площа однієї з частин, наприклад, Р(А) = 2-Д80 < ¡2) = 2-0,091 ~ 0,182 = 18,2%.

Розподіли дають можливість рішення і зворотної задачі: знаходження значень змінної x, ймовірність якої задано.

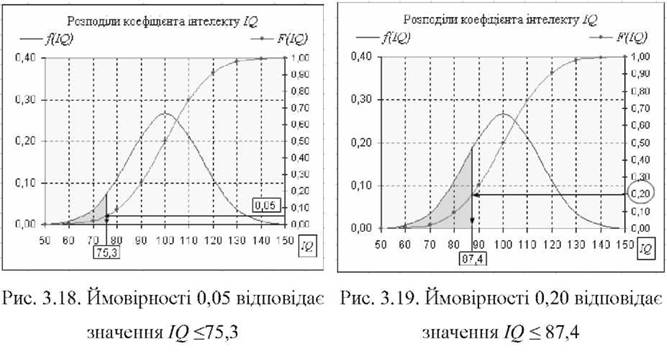
Так, за даними прикладу 3.12 можна стверджувати, що на рівні ймовірності 0,05 (5%) коефіцієнт інтелекту ¡2 не перевищуватиме значення 75,3. З графіка функції розподілу Р(2) рис. 3.18 видно, що ймовірності 0,05 відповідає зафарбована площа, яка обмежена графіком щільностіЛ(Ш) і ординатою ¡2 = 75,3. Інакше кажучи, Р(!2) = ^(¡2 < 75,3) = 0,05.

Аналогічно можна отримати значення змінної ¡2, ймовірність якої складає 20% або 0,20. З рис. 3.19 видно, що ймовірності 0,20 відповідає зафарбована площа, яка обмежена графіком щільностіЛ(Ш) і ординатою ¡2 = 87,4.

Інакше кажучи, Р(!2) = ^(¡2 < 87,4) = 0,20.

На даному етапі вивчення властивостей розподілів доречно згадати поняття "процентиль" і надати йому додаткового змістовного сенсу. Як визначалося вище, процентилі ділять обсяг упорядкованої сукупності на сто частин, тобто відокремлюють від сукупності по 0,01 частки (по 1%). Pj - це z'-й процентиль - межа, нижче за яку лежать /' відсотків значень. Наприклад, якщо п'ятий процентиль дорівнює 30 (записують Р₅ = 30), це значить, що 5% всіх значеньx не перевищують 30.

Значення функції розподілу F(X), які знаходяться у межах від 0 для F(-") до 1 для F(+co), також зручно поділити на сто частин і представляти функцію розподілу у вигляді процентилів. Якщо ціна шкали функції розподілу F(x) становить 0,01 (1%), отримані вище результати можна прокоментувати у такій спосіб:

o для F(IQ) = P(IQ<75,3) = 0,05 = 5% можна записати Р₅ = 75,3 - п'ятому процентилю відповідає коефіцієнт інтелекту, який не перевищує значення у 75,3;

o для F(IQ) = P(IQ <87,4) = 0,20 = 20% можна записати Р₂₀ = 87,4 - двадцятому процентилю відповідає коефіцієнт інтелекту, який не перевищує 87,4.

Значення процентиля для нормального розподілу можна отримати за допомогою функції MS Excel =НОРМОБР(ймовірність; середнє; ст.відхилення). Так, ^₅ = НОРМОБР(0,05;100;15) = 75,3; а Р₂₀ = НОРМОБР(0,20;100;15) = 87,4.