Залежно від способу обгрунтування істинності тези доведення поділяють на прямі та непрямі.
*Прямим називають доведення, в якому істинність тези обґрунтовується, виходячи безпосередньо з аргументів. Застосування правил логічного слідування дає можливість із вихідних формул, які називають аргументами, засновками або припущеннями, виводити нові формули, що логічно слідують із вихідних. Це досягається шляхом побудови послідовних формул, в яких кожна формула є засновком або висновком з попередньої формули за одним із правил слідування.
Розглянемо приклад формального доведення, побудованого за допомогою правила mр. Покажемо, що А —> В, В —> С, А ь С.
Спочатку випишемо аргументи, тобто всі формули, що стоять зліва від знаку "Ь". А потім кожен новий висновок (аргумент) будемо обґрунтовувати правилом mр, записуючи його справа від висновку.
Отже:

Таким чином, теза "С" є доведеною. Останній рядок не нумеруємо для того, щоб показати, що доведення закінчено.
Пряме доведення, як бачимо, являє собою послідовний ряд виводів, в якому висновок кожного з них, крім останнього, входить до складу засновків одного з наступних виводів. Висновок останнього виводу є тезою доведення.
Візьмемо ще один приклад. Побудуємо пряме доведення для такого міркування: (А л В) —> ~С, В л С і—А.

Істинність тези (~А) є доведеною, оскільки кожен висновок (новий аргумент) отриманий нами у ході розмірковування за одним із правил виводу. Часто в міркуваннях висновок (тезу) формулюють як умовне судження (А -" С), тоді антецедент (А) цього твердження використовують як ще один аргумент. Тобто:
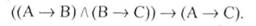
У цьому міркуванні фактично слід довести істинність твердження - "С":
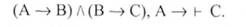
Доведення матиме вигляд:

Побудування прямого доведення тези буває не завжди можливим. Якщо, наприклад, аргументів для прямого доведення недостатньо, то використовують непряме доведення.
4. Непряме доведення
* Непрямим називають доведенням, в якому істинність тези обґрунтовується хибністю антитези. * Антитеза - твердження, яке є хибним тоді і тільки тоді, коли теза є істинною*
При цьому антитеза може бути виражена двоїсто: 1) якщо тезою є твердження "А", то антитезою буде його заперечення - "~А";
2) антитезою для твердження "А", яке входить до складу альтернатив (А Л/ В Л/ С), будуть твердження "В" і "С".
Це двоїсте вираження антитези поділяє непряме доведення на два види: 1) апагогічне (від грецького - ухилення, відведення), тобто доведення методом "від супротивного" та 2) розділове доведення, тобто доведення методом виключення.
1) В апагогічному доведенні замість того, щоб доводити істинність тези "А", припускають істинність антитези "~А" і будують пряме доведення цього твердження. Якщо в ході доведення між будь-якими двома пунктами (твердженнями) виникає суперечність (наприклад, "В" і "-В"), то це означає, що припущення істинності антитези (~А) є помилковим, і істинною є теза (А). Дійсно, з двох суперечливих висловлювань "А" і "-А" лише одне є істинним (закон виключеного третього). Формула (В Л -В) - це формула-суперечність (завжди хибна формула), а вона може бути логічним наслідком тільки хибної формули (~А). Тобто:
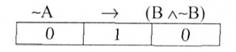
У цьому випадку між "~А" та "В Л-В" існує відношення логічного слідування (~А І- (В Л-В)). У супротивному випадку відношення логічного слідування не існує, бо формула:
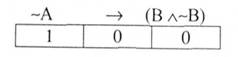
буде завжди хибною.
Таким чином, теза А буде істинною:
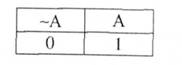
Побудуймо апагогічне доведення для такого міркування:
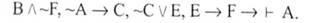
Припустимо, що "~А", тобто що істинною є антитеза.

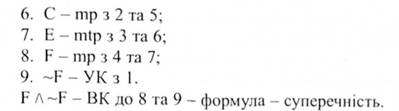
Оскільки між пунктами 8 та 9 виникла суперечність, а кожне з цих тверджень отримане за відповідними правилами виводу, то це означає, що наше припущення істинності антитези "~А" є помилковим. Отже, істинною є теза "А".
1) У розділовому доведенні істинність тези обґрунтовується шляхом послідовного доведення хибності всіх членів розділового висловлювання (диз'юнкції), крім одного.
Наприклад, необхідно довести тезу "Це вчинив А". Маємо такі аргументи (підстави): 1) це могли вчинити тільки А, або В, або С; 2) встановлено, що до цього не причетні ні В, ні С.
Використавши структуру розділово-категоричного виводу (modus tollendo ponens):
Це могли вчинити тільки А, або В, або С.
Ні В. ні С цього не робили.
Це зробив А.
Висновок буде істинним, якщо в розділовому засновку враховано всі можливі альтернативи. Оскільки для modus tollendo ponens смисл сполучника "або" (диз'юнкція чи сильна диз'юнкція) не має значення для правильності виводу, то дане міркування запишемо у вигляді такої структури виводу:
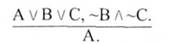
Ця структура виводу є правильною, отже, при істинних засновках висновок теж буде істинним.
6. Правила змістовного доведення