Поняття та галузь застосування
Значна частина економічних завдань, в тому числі й в галузі стратегічного менеджменту, потребує за своїм змістом цілочисельного рішення, коли змінні величини визначають кількість неподільних одиниць продукції, устаткування, заготовок тощо. В багатьох випадках такі завдання вирішуються звичайними методами, наприклад, симплексним, з наступним приведенням до цілих чисел. Але такий підхід виправданий, коли одиниця невимірно мала порівняно з усім обсягом (наприклад, товарних запасів); в іншому випадку цей підхід може суттєво спотворити дійсно оптимальне рішення.
Метод Гоморі для лінійних завдань цілочисельного програмування заснований на понятті конгруентності дійсних чисел. Будь-яке дійсне число можна представити у вигляді суми його цілої та дробової частини: х=[х]+{х}, де квадратні дужки означають цілу частину, а фігурні - дробову. Наприклад, 7,5 = [7,5]+{7,5}=7+0,5.Якщо позначити конгруентність чисел символом є, то, наприклад, 7,5 є 0,5; 6,3 є 0,3.
За методом Гоморі розв'язок цілочисельних задач на першому етапі нічим не відрізняється від простого розрахунку за симплексним алгоритмом. Якщо серед значень змінних в оптимальному плані є дроби, то складається додаткове обмеження, що відсікає частину рішення, але залишаються всі інші умови, які повинен задовольняти оптимальний план. Це додаткове обмеження приєднується до вихідних обмежень задачі, та знову застосовується процедура симплексного методу. Алгоритм Гоморі дозволяє прийти до оптимального цілочисельного рішення за кінцеву кількість кроків.
Приклад застосування
Нехай для придбання устаткування, що розміщується на виробничій площі 38 м2, підприємство виділило 20 тис. грн. Є одиниці устаткування двох типів: тип А вартістю 5 тис. грн., що вимагає 8 м2 виробничої площі та має продуктивність 7 тис. од. продукції за зміну, і тип Б вартістю 2 тис. грн., що вимагає площі в 4 м2 та дає за зміну 3 тис. од. продукції. Потрібно розрахувати оптимальний варіант придбання устаткування, що забезпечує максимум продуктивності виробничої ділянки.
Сформулюємо економіко-математичну модель задачі. Нехай х" х2 - кількість придбаних машин типів А і Б відповідно. Тоді цільова функція задачі матиме такий вигляд:
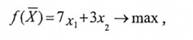
при обмеженнях:
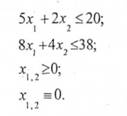
Введемо додаткові змінні Х3, х4, за допомогою яких вихідні нерівності перетворюються в рівності:
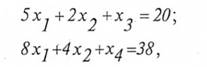
з яких випливає, що змінні х3, х4можуть приймати тільки невід'ємні цілочисельні значення. Симплексна таблиця на останній ітерації (без врахування цілочисельностї) має вигляд:
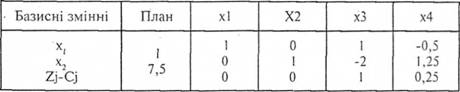
Вона дозволяє підсумувати, що в оптимальному плані х=1; ^=7,5 і максимум цільової функції дорівнює Дх)=71+37,5=29,5.
Для нецілочисельної змінної х2 складемо з наведеної симплексної таблиці рівняння:
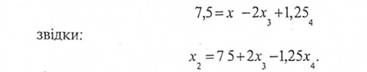
Оскільки х2 - ціле число, то цільовою повинна бути и права частина останнього рівняння (є є символ конгруентності):
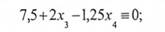
звідки можна отримати, що:
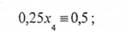
тобто вираз 0,25 х4 може бути рівним 0,5, або 1,5, або 2,5 тощо. Звідки з'являється додаткове обмеження:
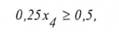
яке шляхом введення додаткової невід'ємної цілочисельної змінної х5
перетворюється в рівність, оскільки система обмежень вихідної задачі в канонічному вигляді містить три рівняння:
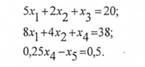
Повторивши процес рішення симплексним методом для даної розширеної системи обмежень, отримаємо новий оптимальний план, в якому змінні, що складають баланс, приймають цілі значення: х, = 2; *2 ~ 5; х4 = 2. Таким чином, придбання двох машин типу А і п'яти машин типу Б забезпечать максимум продуктивності ділянки, що дорівнює 29 тис. од. продукції за зміну. Зазначимо, що якби як план був обраний варіант, отриманий у результаті заокруглення початкового рішення задачі симплексним методом (х, = 1; х, = 7), то сумарна продуктивність була б. рівною лише 28 тис. од.
Література