Психодіагностика - Галян І.М. - Оцінювання достовірності значень за t - критерієм Стьюдента

Найчастіше в психологічному дослідженні спостерігається завдання на виявлення відмінностей між двома або більше групами ознак. З'ясування таких відмінностей на рівні середніх арифметичних розглянуто в процедурі аналізу первинних статистик. Проте виникає питання, наскільки ці відмінності достовірні і чи можна їх поширити (екстраполювати) на всю популяцію. Для розв'язання цього завдання найчастіше використовують (за умови нормального або наближеного до нормального розподілу) t - критерій (критерій Стьюдента), що призначений для з'ясування, наскільки достовірно відрізняються показники однієї вибірки досліджуваних від іншої (наприклад, коли досліджувані одержують внаслідок тестування однієї групи вищі бали, ніж представники іншої). Це параметричний критерій, що має дві основні форми:

1) незв'язаний (непарний) t - критерій, призначений для того, щоб з'ясувати, чи є відмінності між оцінками, отриманими при використанні одного і того самого тесту для тестування двох груп, сформованих з різних людей. Наприклад, це може бути порівняння рівня інтелекту або нервово-психічної стійкості, тривожності встигаючих і невстигаючих учнів або порівняння за цими ознаками учнів різних класів, вікових груп, соціальних рівнів тощо. Можуть бути і різностатеві, різнонаціональні вибірки, а також підвибірки в досліджуваних вибірках, виокремлені за певною ознакою. Критерій називають "незв'язаний", тому що порівнювані групи сформовані з різних людей;

2) зв'язаний (парний) t - критерій, що застосовують для порівняння показників двох груп, між елементами яких існує специфічний зв'язок. Це означає, що кожному елементу першої групи відповідає елемент другої групи, схожий на нього за певним параметром, що цікавить дослідника. Найчастіше порівнюють параметри одних і тих самих осіб до і після певної події або дії (наприклад, у процесі проведення лонгітюдного дослідження або формувального експерименту). Тому цей критерій використовують для порівняння показників одних і тих самих осіб до і після обстеження, експерименту або закінчення певного часу.

Якщо дані не підлягають нормальному закону розподілу, використовують непараметричні критерії, еквівалентні t - критерію: критерій Манна - Вітні, еквівалентний непарному t - критерію, і двохвибірковий критерій Вілкоксона, еквівалентний парному t - критерію.

За допомогою t - критеріїв і їх непараметричних еквівалентів можна лише порівнювати результати двох груп, отримані з використанням одного і того самого тесту. Проте в деяких випадках виникає необхідність порівняння кількох груп або оцінок кількох видів. Це можна зробити поетапно, розбивши задачу на кілька пар порівнянь (наприклад, якщо треба порівняти групи А, Б і Y за результатами тестів X і У, то можна за допомогою t - критерію спочатку порівняти групи А і Б за результатами тесту X, потім А і Б за результатами тесту У, А і В за результатами тесту Х і т. д.). Проте це дуже трудомісткий метод, тому вдаються до складнішого методу дисперсійного аналізу.

Метод оцінювання достовірності відмінностей середніх арифметичних за достатньо ефективним параметричним критерієм Стьюдента призначений для розв'язання одного із завдань, що найчастіше спостерігаються при обробленні даних - виявлення достовірності відмінностей між двома або більше рядами значень. Таке оцінювання часто необхідне при порівняльному аналізі полярних груп. їх виокремлюють на основі різної вираженості певної цільової ознаки (характеристики) явища, що вивчається. Як правило, аналіз починають з підрахунку первинних статистик виділених груп", потім оцінюють достовірність відмінностей. Критерій Стьюдента обчислюють за формулою:

Значення критерію Стьюдента для трьох рівнів довірчої (статистичної) значущості (р) наводять у довідниках з матстатистики. Кількість ступенів свободи визначають за формулою:

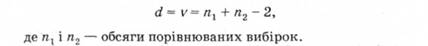
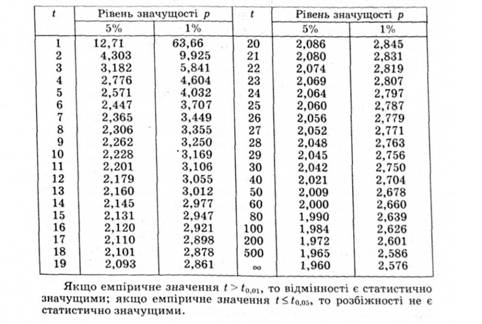
Із зменшенням обсягів вибірок (n < 10) критерій Стьюдента стає чутливим до форми розподілу досліджуваної ознаки в генеральній сукупності. Тому в сумнівних випадках рекомендують використовувати непараметричні методи або порівнювати отримані значення з критичними (табл. 2.17) для вищого рівня значущості.

Рішення про достовірність відмінностей приймають у тому разі, якщо обчислена величина t перевищує табличне значення для певної кількості ступенів свободи (d(v)). У публікаціях або наукових звітах вказують найвищий рівень значущості з трьох: р < 0,05; р < 0,01; р< 0,001.

За будь-якого числового значення критерію достовірності відмінності між середніми цей показник оцінює не ступінь виявленої відмінності (її оцінюють за самою різницею між середніми), а лише його статистичну достовірність, тобто право поширювати отриманий на основі зіставлення вибірок висновок про наявність різниці на все явище (весь процес) загалом. Низький обчислений критерій відмінності не може бути доказом відсутності відмінності між двома ознаками (явищами), бо його значущість (ступінь вірогідності) залежить не тільки від величини середніх, а й від кількості порівнюваних вибірок. Він вказує не на відсутність відмінності, а на те, що за такої величини вибірок вона статистично недостовірна: дуже великий шанс, що різниця за цих умов випадкова, дуже мала вірогідність її достовірності.

Таблиця 2.17. Довірчі межі для критерію Стьюдента (t-критерій) для f ступенів свободи

рення середнього часу виконання завдання в другій спробі (порівняно з першою пробою) не є достовірним.

Це вираження не рівносильне твердженню про статистичну однорідність двох вибірок, які зіставляють. Крім того, застосування критерію Стьюдента у разі таких неоднакових вибірок не цілком коректне математично і, безперечно, позначається на кінцевому висновку про невірогідність відмінностей Хср = 9,1 і Хср = 8,5. Послуговуючись цим критерієм, оцінюють не ступінь близькості двох середніх, а розглядають щодо віднесення або невід несення до випадкової (за заданого рівня значущості). .