Логіка - Мозгова Н.Г. - Короткий зміст розділу

Короткий зміст розділу

Складне судження (висловлювання) є об'єктом вивчення розділу логіки, який називають *логікою висловлювань. Логіка висловлювань є важливою частиною сучасної формальної логіки, оскільки саме на цій теорії ґрунтуються інші складові логіки.

1. Поняття складного висловлювання

Висловлювання, яке містить у собі інші висловлювання як складові частини, називають *складними. Якщо жодна частина даного висловлювання не може розглядатися як самостійне висловлювання, то воно називається простим, або елементарним. Складне висловлювання, таким чином, включає в себе прості.

У логіці висловлювань не розглядають і не враховують внутрішню структуру елементарних висловлювань - розчленування на суб'єкт та предикат. Тому прості висловлювання називають ще атомарними, або атомами (від грецького — неподільний), a складні - молекулярними, або молекулами (від латинського moles - шматок; частинка речовини, що складається з атомів) (аналогія з хімією тут суто зовнішня).

Логіка висловлювань відволікається також і від змісту висловлювання або його смислу, розглядаючи будь-яке висловлювання (атом чи молекулу) як істинне (1), або хибне (0).

Атомарні висловлювання позначають літерами - А, В, С, N або однією літерою з індексом - А,, А2, Аn. Ці літери називають пропозиційними (від латинського propositio - речення, висловлювання) змінними, оскільки їм відповідають різні за змістом елементарні висловлювання.

2. Логічні сполучники та логічні операції

Основними питаннями дослідження логіки висловлювань є:

1) як з атомарних висловлювань утворюються молекулярні;

2) як залежить значення істинності молекули від значень істинності атомів, які її складають.

Складні висловлювання утворюються з елементарних за допомогою логічних сполучників (пропозиційних зв'язок), яким відповідають логічні операції, що позначаються відповідними символами логічних операцій або логічними операторами. Цей зв'язок можна зобразити в таблиці:

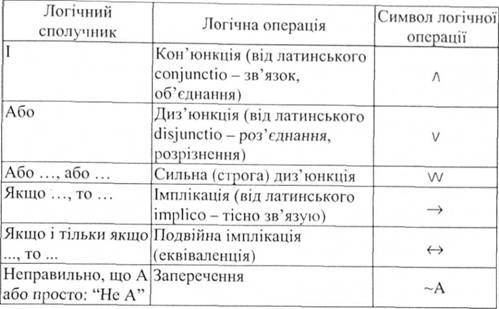
Утворення нових висловлювань із вихідних за допомогою логічних сполучників називають логічними операціями. Кожна логічна операція визначається так, що значення істинності молекулярного висловлювання залежить лише від значень істинності складаючих його атомів, а не від їх змісту чи смислової характеристики отриманого висловлювання.

Логічну операцію та її результат позначають одним і тим же словом. Наприклад, кон'юнкція, диз'юнкція тощо. Визначення операцій дають у вигляді таблиць (матриць) істинності, в яких подаються значення істинності молекули при всіх можливих комбінаціях значень істинності складаючих її атомів.

Якщо в молекулу входять п утворюючих її атомів, то для них можливі 2" різних комбінацій значень істинності атомів і таблиця істинності молекули буде складатися із 2" рядків.

Для того, наприклад, щоб правильно побудувати таблицю істинності для молекули з трьох (А,В,С) атомів, необхідно дотримуватися такого алгоритму:

1) обрахувати кількість рядків у таблиці: 23 = 8;

2) у першому лівому стовпчику значення істинності розподіляється так: 8: 2 = 4, тобто перші чотири - "істина (1)", а чотири наступні - "хиба (0)";

3) другий стовпчик - 4: 2 = 2 і т. д.

Побудована нами матриця відповідає двом необхідним умовам: 1) вона включає всі можливі комбінації значень істинності атомів, тобто є вичерпною; 2) жодна з цих комбінацій не повторює іншу.

Враховуючи ці вимоги, дамо визначення логічним операціям.

1) Кон'юнкція.

Кон'юнкцією висловлювань А та В називають висловлювання А/В (читається "А і В"), яке є істинним тоді і тільки тоді, коли істинними є всі атоми. Цьому визначенню відповідає таблиця:

Наприклад, "Я склав залік з логіки (А) та історії України (В)". Якщо обидва ці висловлювання є істинними, то й молекулярне висловлювання - істинне (1-ий рядок матриці). В усіх інших випадках - коли істинне лише одне висловлювання, або обидва є хибними - висловлювання в цілому є хибним (2, 3,4 рядки).

Формулі АЛВ відповідають також вислови: "А разом з В", "як А, так і В", "і А, і В", "А в той же час, як і В" тощо.

2) Диз'юнкція.

Диз'юнкцією висловлювань А та В називають висловлювання АмВ (читають "А або В"), яке є істинним тоді і тільки тоді, коли принаймні один з атомів є істинним. Визначенню відповідає таблиця:

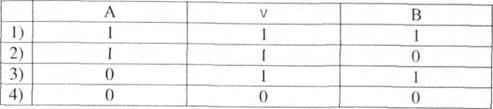
Наприклад, "Буду читати підручник (А) або складати з нього конспект (В)". Ці дії можуть виключати одна одну і висловлювання буде істинним (2,3 рядок). Але ці дії можуть відбуватися й одночасно, тоді висловлювання буде теж істинним (1 рядок). Але, якщо жодне з тверджень не відповідає дійсності (є хибним, 4 рядок), то і висловлювання в цілому буде хибним.

У наведеному прикладі сполучник "або" використовується в з'єднувально-роз'єднувальному смислі, тобто "А або В, або обидва”. Цьому смислу відповідають також: "А і/або В", "і А, і В чи А або В", "А, якщо не В" тощо.

В українській мові (як і в багатьох інших) сполучник "або" може використовуватись і в суто роз'єднувальному сенсі, тобто "або або ...". Цей смисл відповідає логічній операції сильної (строгої) диз'юнкції.

3) Сильна диз'юнкція.

Сильною диз'юнкцією висловлювань А та В називають висловлювання А^В (читають и або А, або В"), яке є істинним тоді і тільки тоді, коли тільки один з атомів є істинним. Цьому визначенню відповідає таблиця:

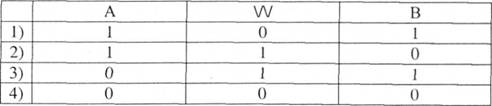
Наприклад, "Піду в кіно (А) або в бібліотеку (В)". Зрозуміло, що ці твердження не можуть бути одночасно істинними (1 рядок), бо людина не може бути одночасно в двох різних місцях. Висловлювання в цілому буде хибним і тоді, коли ці твердження є одночасно хибними (4 рядок). Молекула буде істинною тільки тоді, коли лише один атом є істинним.

Формулі AwB відповідають вислови: "А або В, але не обоє", "чи А, чи В", "А, крім випадку, коли В" тощо.

Оскільки твердження А та В є взаємовиключними, то їх називають альтернативами (від латинського alterno - чергую, змінюю).

4) Імплікація.

Імплікацією висловлювань А та В називають висловлювання А—)В (читають "якщо А, то В "), яке є хибним тоді і тільки тоді, коли А істинне, а В хибне. Визначенню відповідає таблиця:

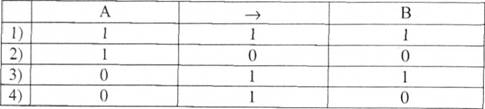
Імплікація відображає різні відношення між простими судженнями. Зокрема, відношення підпорядкування (А, Е -1, О), коли, наприклад, з істинного загального судження випливає істинне часткове і це відношення в цілому є істинним (1 рядок). "Якщо всі юристи знають логіку, то і деякі юристи знають логіку". Але, якщо загальне судження є істинним, то часткове не може бути хибним (2 рядок). Таке висловлювання в цілому буде хибним.

В імплікації А-"В ліва частина А називається антецедентом (від латинського antecedens - попередній), а права - консеквентом (від латинського consequens - наступний). Формулі імплікації відповідають вислови: "А тоді, коли В", "оскільки А, то В", "у випадку А і В", "А імплікує В" тощо.

Слід розрізняти матеріальну імплікацію та умовне висловлювання.

В умовному висловлюванні ліва частина зумовлює праву, тобто вони знаходяться в певній смисловій та змістовій залежності. Наприклад, "Якщо воду охолодити до 0 °С, то вона перетвориться на лід". У матеріальній імплікації ліва та права частини можуть не знаходитись у залежності, а лише пов'язані сполучником "якщо то..." Наприклад, "Якщо вчора була гарна погода, то сьогодні зранку йде дощ".

5) Подвійна імплікація.

Подвійною імплікацією (еквіваленцією) висловлювань А та В називають висловлювання А"-"В (читають "якщо і тільки якщо А, то В"), яке є істинним тоді і тільки тоді, коли значення істинності атомів збігаються. Визначенню відповідає таблиця:

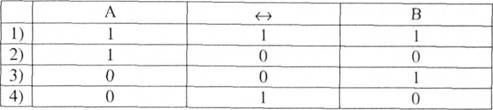
Подвійна імплікація є таким відношенням між атомарними висловлюваннями, коли з А випливає В, а з В випливає А. Тобто, при правильно визначеному відношенні між А а В ці судження будуть рівнозначними. Це відоме вже нам виділяюче судження. Наприклад, "Якщо і тільки якщо геометрична фігура є квадратом, то вона є рівнобічним прямокутником". Якщо поміняти ліву та праву частини висловлювання, то його смисл не зміниться.

Оскільки логіка висловлювань відволікається від предметного змісту атомів, то важливим для нас є значення істинності подвійної імплікації. 1) Якщо вона є істинною, то це означає, що обидва атоми є одночасно або істинними, або хибними. 2) Якщо вона є хибною, то це означає, що значення істинності атомів є протилежним.

6) Заперечення.

Запереченням висловлювання А називають висловлювання ~А (читають "неправильно, що А" або просто "не А"), яке є істинним, коли А - хибне, і навпаки. Цьому визначенню відповідає таблиця:

З таблиці видно, що два суперечливих твердження завжди мають протилежні значення істинності.

Використовуючи пропозиційні змінні та символи логічних операцій, будь-яке висловлювання можна *формалізувати, тобто замінити формулою логіки висловлювань, яка буде відображати його структуру.

Наприклад, "Неправильно, що коли зберуться Петро та Микола, то вони будуть грати в шахи".

У структурі цього висловлювання с три атоми:

А - буде Петро;

В - буде Микола;

С - вони будуть грати в шахи, та такі логічні операції: заперечення (~); коли (якщо)..., то ... (—>);... та(і)...(л).

Отже, структура цього висловлювання:

-(А Л В) -> С.

Читаємо: "Неправильно, що, якщо А і В, то С". Зрозуміло, що ця формула відображає множину висловлювань такого типу, бо А, В. С можуть символізувати різні за змістом твердження.